Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

a. Ta có: $3 x-4=5+x$

$3 x-x=5+4$

$2 x=9$

$x=\dfrac{9}{2}$.

Vậy phương trình đã cho có nghiệm $x=\dfrac{9}{2}$.

b. Ta có: $3(x-1)-7=5(x+2)$

$3 x-3-7=5 x+10$

$5 x-3 x=-3-7-10$

$2 x=-20$

$x=-10$.

Vậy phương trình có nghiệm $x=-10$.

Hướng dẫn giải:

Gọi vận tốc riêng của ca nô là $x$ (km/h, $x>3$).

Vận tốc ca nô khi đi xuôi khúc sông từ $A$ đến $B$ là: $x+3$ (km/h);

Vận tốc ca nô khi đi ngược khúc sông từ $B$ về $A$ là: $x-3$ (km/h);

Khúc sông $A B$ có chiều dài không đổi nên ta có phương trình: $\dfrac{3}{2}(x+3)=2(x-3)$.

Giải phương trình trên ta nhận được $x=21$ (thỏa mãn)

Do đó vận tốc riêng của ca nô là $21$ km/h.

Chiều dài khúc sông là: $2(21-3)=36$ (km).

Vậy vận tốc riêng của cano là $21$ km/h, chiều dài khúc sông là $36$ km .

Hướng dẫn giải:

Xác suất cho biến cố "Thẻ rút ra là thẻ đánh số 3" là: $\dfrac{6}{20}=\dfrac{3}{10}$.

Hướng dẫn giải:

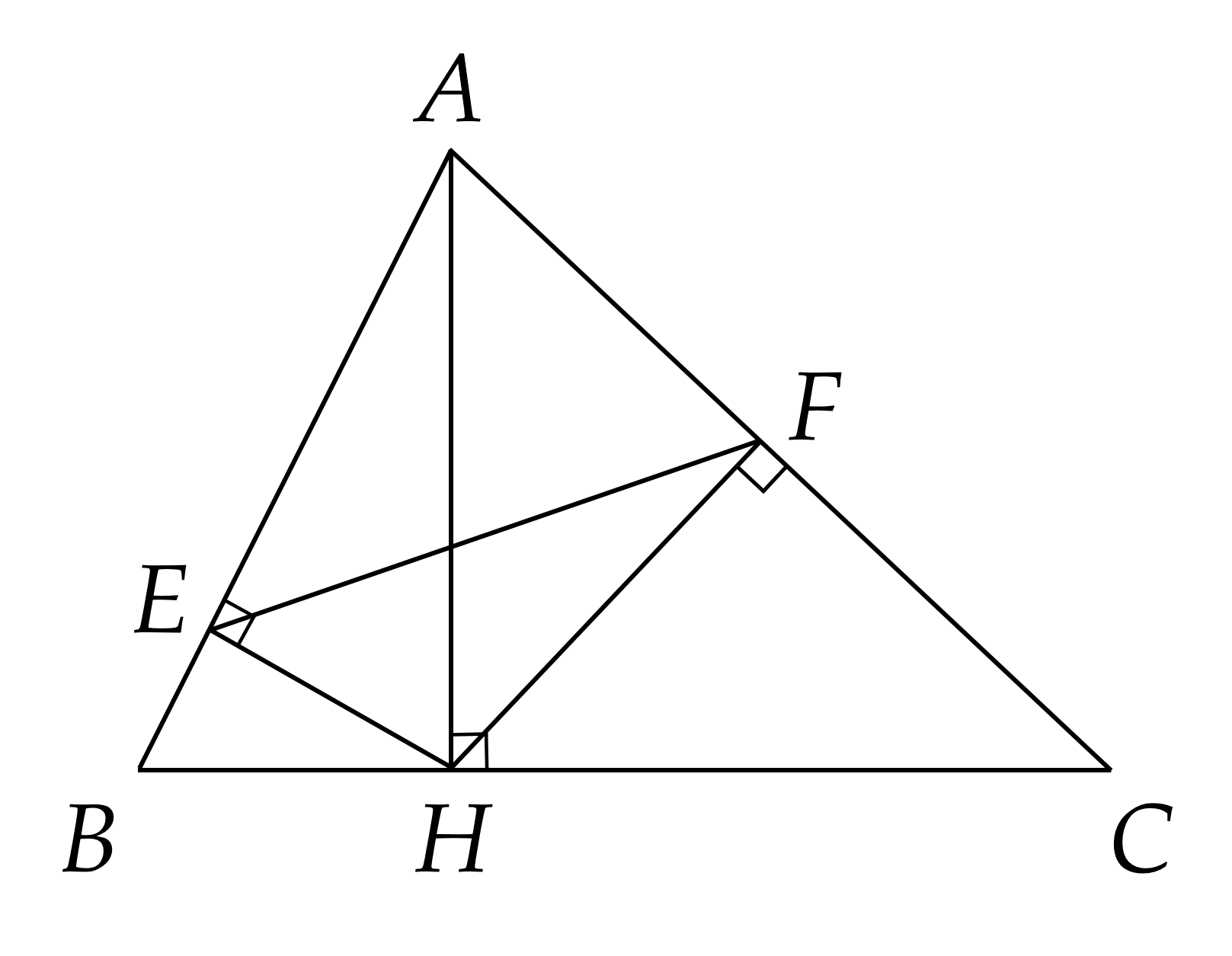
a) Xét $\Delta { A E H}$ và $\Delta { A H B}$ có:

$\widehat{BAH}$ chung và $\widehat{AEH}=\widehat{AHB}=90^{\circ}$

Do đó $\Delta {AEH} \backsim \Delta {AHB}$ (g.g)

Suy ra $ \dfrac{A H}{A B}=\dfrac{A E}{A H} $ hay $A H^2=A E .A B$ (1)

b) Chứng minh tương tự $\Delta {AHF} \backsim \Delta {ACH}$ (g.g) 

Suy ra $\dfrac{A H}{A C}=\dfrac{A F}{A H}$ hay $A H^2=A F . A C$ (2)

Từ (1) và (2) suy ra $A E . A B=A F . A C$

c) Ta có $A E . A B=A F . A C$ nên $\dfrac{A E}{A C}=\dfrac{A F}{A B}$.

Xét $\Delta { A E F}$ và $\Delta { A C B}$ có:

$\widehat{E A F}$ chung

$\dfrac{A E}{A C}=\dfrac{A F}{A B}$ (cmt)

Do đó $\Delta { A E F} \backsim \Delta { A C B} $ (c.g.c).

Suy ra $\dfrac{E F}{C B}=\dfrac{P_{A E F}}{P_{A C B}}=\dfrac{20}{30}=\dfrac{2}{3}$ (tỉ số chu vi bằng tỉ số đồng dạng)

Áp dụng tính chất dãy tỉ số bằng nhau ta có $ \dfrac{S_{A E F}}{4}=\dfrac{S_{A C B}}{9}=\dfrac{S_{A C B}-S_{A E F}}{9-4}=\dfrac{25}{5}=5$

Suy ra

$S_{A E F}=5.4=20$ cm$^2$;

$S_{A C B}=5.9=45$ cm$^2$.

Vậy $S_{A E F}=20$ cm$^2$ và $S_{A C B}=45$ cm$^2$.

Hướng dẫn giải:

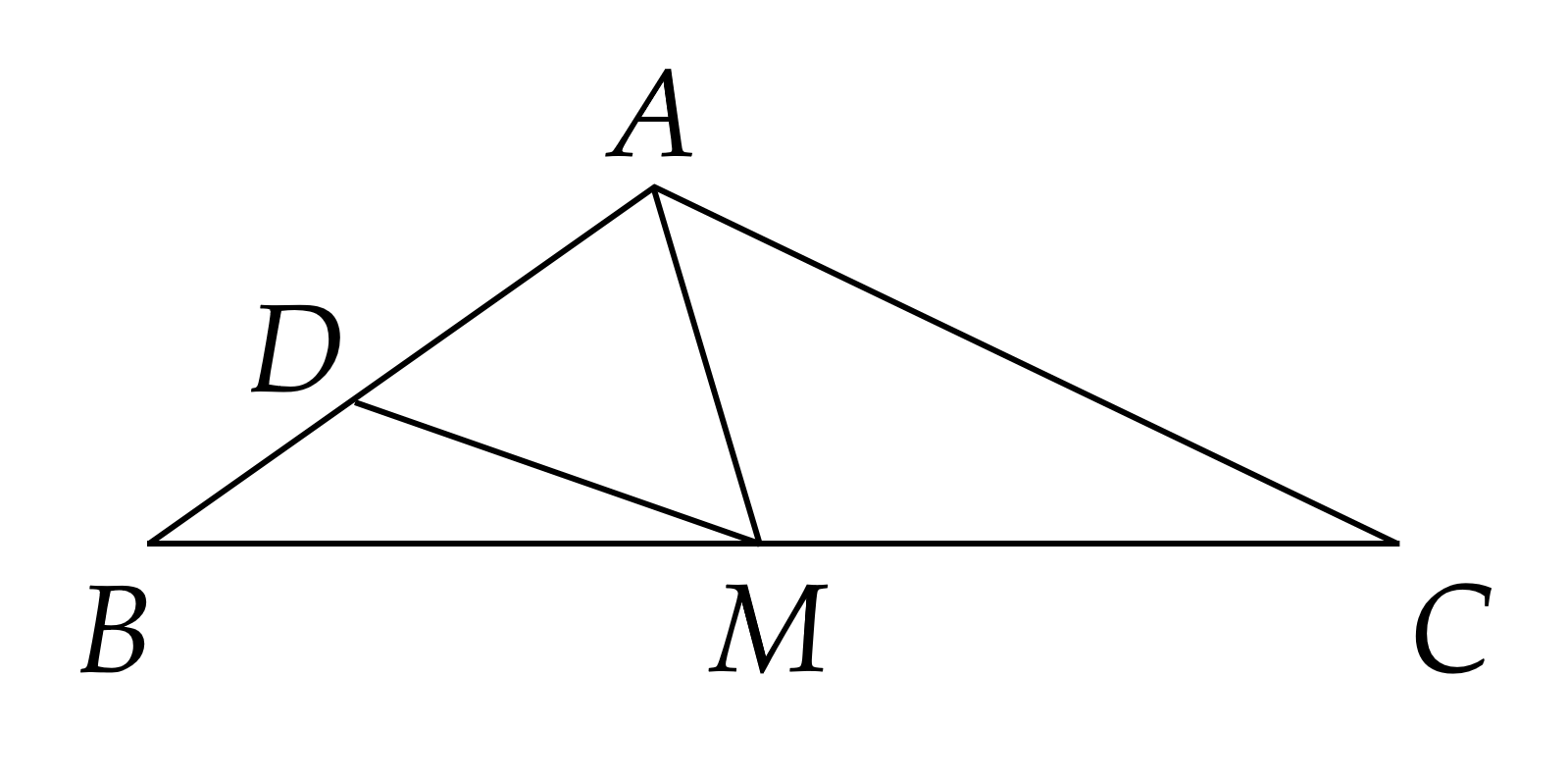
Ta có: $A B=A D+D B$

Suy ra $D B=A B-A D=10-6=4$ cm

${AM}$ là trung tuyến của $\Delta A B C$ suy ra $M$ là trung điểm của ${BC}$

Suy ra $BM=C M=\dfrac{1}{2} B C=15$ cm.

 Xét $\Delta A B M$ có $M D$ là phân giác của góc $A M B$ nên

$\dfrac{A M}{B M}=\dfrac{A D}{D B}$

$\dfrac{A M}{B M}=\dfrac{6}{4}=\dfrac{3}{2} $

Do đó $A M=\dfrac{3}{2} .B M=\dfrac{3}{2} .15=22,5$ (cm).

Hướng dẫn giải:

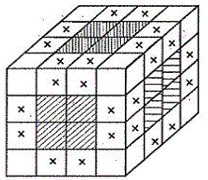
a) Ở mỗi mặt, có $4$ hình lập phương nhỏ được sơn một mặt (các hình được gạch sọc).

Ở sáu mặt có: $4.6  = 24$ (hình).

b) Ở mỗi cạnh, có $2$ hình lập phương được sơn hai mặt (các hình ghi dấu "$x$").

Ở $12$ cạnh có : $2.12=24$ (hình).