Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
Bài 1. (1 điểm) Giải các phương trình sau:
a) $2 x=7+x$.
b) $\dfrac{x-3}{5}+\dfrac{1+2 x}{3}=6$.
Hướng dẫn giải:
a) $2 x=7+x$
$2x - x = 7$
$x = 7$.
Phương trình đã cho có nghiệm $x = 7$.
b) $\dfrac{x-3}{5}+\dfrac{1+2 x}{3}=6$
$\dfrac{3(x-3)}{15}+\dfrac{5.(1+2x)}{15}=6$
$3x - 9 + 5 + 10x = 90$
$13x = 94$
$x =\dfrac{94}{13}$.
Phương trình đã cho có nghiệm $x = \dfrac{94}{13}$.
Bài 2. (2,0 điểm)
1) Cho hai đường thẳng sau: $\left(d_1\right): \, y=-3 x$; $\left(d_2\right): \, y=x+2$.
a) Vẽ đường thẳng $\left(d_1\right)$ trên mặt phẳng tọa độ $O x y$.
b) Tìm $a, \, b$ để đường thẳng $\left(d_3\right): \, y=a x+b$ đi qua điểm $A(-1 ; 3)$ và song song với $\left(d_2\right)$.
2) Theo kế hoạch hai tổ sản xuất phải làm $900$ sản phẩm. Do cải tiến kĩ thuật nên tổ I vượt mức $20\%$ và tổ II vượt mức $15\%$ so với kế hoạch. Do đó trên thực tế hai tổ đã sản xuất được $1$ $055$ sản phẩm. Hỏi theo kế hoạch mỗi tổ sản xuất được bao nhiêu sản phẩm?
Hướng dẫn giải:
1)
a) Xét đường thẳng: $\left(d_1\right): \, y=-3 x$.
Nếu $x=0$ thì $y=0$ suy ra $\left(d_1\right)$ đi qua điểm có tọa độ $(0 ; 0)$
Nếu $x=1$ thì $y=-3$ suy ra $\left(d_1\right)$ đi qua điểm có tọa độ $(1 ;-3)$
Ta vẽ đồ thị:
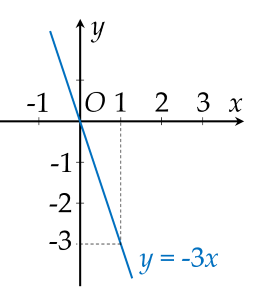
b) Vì $\left(d_3\right): \, y=a x+b$ song song với $\left(d_2\right): \, y=x+2$ nên $a=1, \, b \neq 2$.
Khi đó đường thẳng $\left(d_3\right)$ có dạng $y=x+b$ với $b \neq 2$.
Vì $\left(d_3\right)$ đi qua điểm có tọa độ $A(-1 ; 3)$ nên: $3=-1+b$ hay $b=3+1=4$ (thỏa mãn).
Vậy đường thẳng $\left(d_3\right)$ là $\left(d_3\right): y=-x+4$.
2) Gọi số sản phẩm mà tổ I làm được theo kế hoạch là $x$.
Điều kiện: $x \in \mathbb{N}^*$; $x < 900$, đơn vị: sản phẩm.
Số sản phẩm mà tổ II làm được theo kế hoạch là: $900-x$ (sản phẩm).
Theo bài ra, do cải tiến kĩ thuật nên tổ một vượt mức $20\%$ và tổ hai vượt mức $15\%$ so với kế hoạch.
Số sản phẩm mà tổ I làm được theo thực tế là: $x+x . 20 \%=x+0,2 x=1,2 x$ (sản phẩm);
Số sản phẩm mà tổ II làm được theo thực tế là: $900-x+(900-x) .15 \%=1 \, 035-1,15 x$ (sản phẩm).
Vì thực tế hai tổ đã sản xuất được $1 \, 055$ sản phẩm nên ta có phương trình: $1,2 x+1 \, 035-1,15 x=1 \, 055$
Giải phương trình tìm được $x=400$ (sản phẩm)
Khi đó, số sản phẩm mà tổ II làm được theo kế hoạch là: $900-400=500$ (sản phẩm).
Vậy theo kế hoạch tổ I làm được $400$ sản phẩm, tổ II làm được $500$ sản phẩm.
Bài 3. (1,0 điểm) Một túi đựng $19$ viên bi cùng khối lượng và kích thước, chỉ khác màu, trong đó có $8$ viên bi màu đỏ, $5$ viên bi màu xanh và $6$ viên bi màu vàng. Lấy ngẫu nhiên một viên bi từ trong túi. Tính xác suất của biến cố "Lấy được viên bi màu đỏ".
Hướng dẫn giải:
Có $19$ kết quả cho hành động trên.
Có $8$ kết quả thuận lợi cho biến cố đã cho nên xác suất cho biến cố là: $\dfrac{8}{19}$.
Bài 4. (2,5 điểm) Cho tam giác $K B C$ vuông tại $K$ ($K B < K C$). Tia phân giác của $\widehat{B}$ cắt cạnh $K C$ tại $H$. Qua $C$ vẽ đường thẳng vuông góc với tia $BH$ cắt đường thẳng $BH$ tại $I$.
a) Chứng minh tam giác $BHK$ đồng dạng với tam giác $CHI$.
b) Chứng minh $CI^2=IH.IB$.
c) Tia $B K$ cắt tia $CI$ tại $A$, tia $A H$ cắt $B C$ tại $D$. Chứng minh $K C$ là tia phân giác của $\widehat{I K D}$.
Hướng dẫn giải:
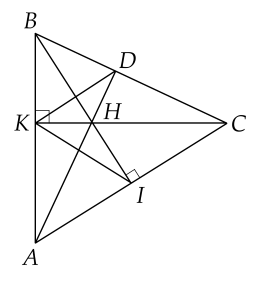
a) Vì tam giác $K B C$ vuông tại $K$ suy ra $\widehat{K B H}=90^{\circ}$
Vì ${CI} \perp {BI}$ (gt) suy ra $\widehat{{ClH}}=90^{\circ}$
Xét $\triangle K B H$ và $\triangle C H I$ có:
$\widehat{{KBH}}=\widehat{{CIH}}=90^{\circ}$;
$\widehat{{BHK}}=\widehat{{CHI}}$ (đối đỉnh)
Suy ra $\Delta {BHK} \backsim \Delta {CHI}$ (g.g)
b) Ta có $\Delta {BHK} \backsim \Delta {CHI}$ suy ra $\widehat{{HBK}}=\widehat{{HCI}}$ (hai góc tương ứng)
Mà ${BH}$ là tia phân giác của $\widehat{{ABC}}$ nên $\widehat{{HBK}}=\widehat{{HBC}}$.
Do đó $\widehat{{HBC}}=\widehat{{HCI}}$.
Xét $\triangle {CIB}$ và $\triangle {HIC}$ có:
$\widehat{{CIB}}$ chung;
$\widehat{{IBC}}=\widehat{{HCI}}$ (cmt)
Vậy $\Delta {CIB} \approx \Delta {HIC}$ (g.g) suy ra $\dfrac{{CI}}{{HI}}=\dfrac{{IB}}{{IC}}$
Hay ${CI}^2={HI} . {IB}$
c) Xét $\triangle {ABC}$ có ${BI} \perp {AC}$; ${CK} \perp {AB}$; ${BI} \cap {CK}=\{{H}\}$
Nên $H$ là trực tâm $\triangle A B C$ suy ra $A H \perp B C$ tại $D$.
Từ đó ta có $\triangle B K C \backsim \triangle H D C$ (g.g) nên $\dfrac{C B}{C H}=\dfrac{C K}{C D} $
Suy ra $\dfrac{C B}{C K}=\dfrac{C H}{C D}$ nên $\triangle {BHC} \backsim \triangle {KDC}$ (c.g.c)
Khi đó $\widehat{{HBC}}=\widehat{{DKC}}$ (hai góc tương ứng)
Chứng minh tương tự $\widehat{{HAC}}=\widehat{{IKC}}$
Mà $\widehat{{HAC}}=\widehat{{HBC}}$ (cùng phụ $\widehat{{ACB}}$ )
Suy ra $ \widehat{{DKC}}=\widehat{{IKC}}$.
Vậy $K C$ là tia phân giác của $\widehat{I K D}$.
Bài 5. (1 điểm) Bạn Đô làm một cái lồng đèn quả trám là hình ghép từ hai hình chóp tứ giác đều giống nhau có cạnh đáy $20$ cm, cạnh bên $32$ cm. Khoảng cách giữa hai đỉnh của hai hình chóp là $30$ cm.
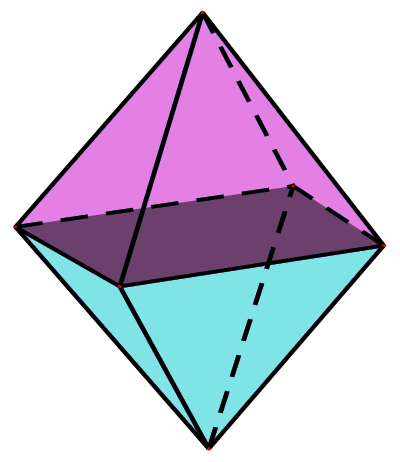
Tính thể tích của lồng đèn.
Hướng dẫn giải:
Chiều cao của mỗi hình chóp tứ giác đều là:
$30:2=15$ (m).
Thể tích của lồng đèn quả trám là:
$V=2.\Big( \dfrac{1}{3}.20.20.15 \Big)=4 \, 000$ (cm$^3$).
Bài 6. (0,5 điểm) Tính diện tích tam giác có độ dài ba cạnh bằng $10$ cm, $17$ cm, $21$ cm.
Hướng dẫn giải:
Xét $\Delta ABC$ có $AB=10$ cm, $AC=17$ cm, $BC=21$ cm.
Gọi $AH$ là đường cao của tam giác.

Vì $BC$ là cạnh lớn nhất của tam giác nên $\widehat{{B}}, \widehat{{C}} < 90^{\circ}$, do đó ${H}$ nằm giữa ${B}$ và ${C}$.
Đặt ${HC}={x}, \, {HB}={y}$, ta có : $x+y=21$ (1)
Mặt khác ${AH}^2=10^2-{y}^2, \, {AH}^2=17^2-{x}^2$ nên $x^2-y^2=17^2-10^2=289-100=189$ (2)
Từ (1) và (2) suy ra ${x}+{y}=21$, ${x}-{y}=9$.
Do đó ${x}=15$, ${y}=6$.
Ta có ${AH}^2=10^2-6^2=64$ nên ${AH}=8$.
Vậy ${S}_{{ABC}}=\dfrac{21.8}{2}=84$ (cm$^2$).
