Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

a) Thị trường Thái Lan cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 là nhiều nhất.

Thị trường Trung Quốc cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 là ít nhất.

b) Tỉ số phần trăm thị trường Indonexia cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 so thị trường Lào là $\dfrac{3 \, 447}{2 \, 983} . 100\% = 115,6\%$.

Thị trường Indonexia cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 tăng $15,6\%$ so thị trường Lào.

c) Trong 9 tháng năm 2022, Việt Nam là thị trường cung cấp tinh bột sắn lớn thứ hai cho thị trường Đài Loan. (đứng sau thị trường Thái Lan).

Thị trường Lào cung cấp tinh bột sắn chiếm số phần trăm so với tổng lượng tinh bột sắn nhập khẩu cho thị trường Đài Loan là: $\dfrac{2 \, 983}{249 \, 927} . 100\% = 1,2\%$.

Vậy nhận định của bài báo đó là chính xác.

Hướng dẫn giải:

a) Có $190$ cách viết ngẫu nhiên một số tự nhiên như vậy.

b) 

+ Có $19$ kết quả thuận lợi cho biến cố "Số tự nhiên được viết ra là số chia hết cho 2 và 5" là:

10; 20; 30; 40; 50; 60; 70; 80; 90; 100; 110; 120; 130; 140; 150; 160; 170; 180; 190.

Xác suất của biến cố đó là: $\dfrac{19}{190} = \dfrac1{10}$.

+ Có $11$ kết quả thuận lợi cho biến cố "Số tự nhiên được viết ra là bình phương của một số tự nhiên" là: 16; 25; 36; 49; 64; 81; 100; 121; 144; 169; 196.

Xác suất của biến cố đó là: $\dfrac{11}{190}$.

Hướng dẫn giải:

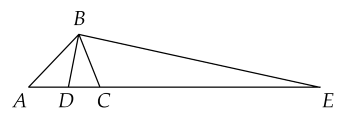
a) Ta có $AD+DC=AC=AB=15$ cm và $\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{15}{10}=\dfrac{3}{2}$.

Suy ra $\left\{\begin{aligned}&A D+D C=15 \\ &A D=\dfrac{3}{2} DC\\ \end{aligned}\right.$.

Từ đó suy ra $AD=9$ cm, $DC=6$ cm.

b) Vì $B D \perp B E$ nên $B E$ là phân giác ngoài của góc $B$ của tam giác $A B C$.

Khi đó ta có $\dfrac{A E}{E C}=\dfrac{A B}{B C}$.

Suy ra $E C=\dfrac{A E . B C}{A B}=\dfrac{A E . 10}{15}=\dfrac{A E . 2}{3}$.

Suy ra $3 . C E=2 . (A C+C E)$ hay $C E=2 .A C$.

Do đó $C E=30$ cm.

Hướng dẫn giải:

Ta có: $4 H(x)=(2 x)^2-2.2 x . y+y^2+3 y^2-4 x+4 y+4$

$=(2 x-y)^2-2(2 x-y)+3 y^2+2 y+3+1$

$=(2 x-y-1)+3\left(y^2+\dfrac{2}{3} y+1\right) $

$=(2 x-y-1)+3\left(y+\dfrac{1}{2}\right)^2+\dfrac{8}{3} \geq \dfrac{8}{3}$.

Vậy giá trị nhỏ nhất của $E$ là: $\dfrac{8}{3} \, : \, 4=\dfrac{2}{3}$ tại $x=\dfrac{2}{3} ; \, y=-\dfrac{1}{3}$