Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

a) $\left(6 x^{3} y^{2}-27 x^{3} y\right) \, : \, 3 x y=2 x^{2} y-9 x^{2}$.

b) $\left(\dfrac{2}{3^{2}} x^{4}\right) .\left(3 y x^{5}\right)=\left(\dfrac{2}{9}.3\right)\left(x^{4} \cdot x^{5}\right) y=\dfrac{2}{3} x^{9} y$.

c) $\dfrac{x^{2}}{x^{2}-4}+\dfrac{1}{x-2}+\dfrac{1}{x+2}=\dfrac{x^{2}}{(x-2)(x+2)}+\dfrac{x+2}{(x-2)(x+2)}+\dfrac{x-2}{(x-2)(x+2)}=\dfrac{x^{2}+x+2+x-2}{(x-2)(x+2)}=\dfrac{x^{2}+2 x}{(x-2)(x+2)}=\dfrac{x(x+2)}{(x-2)(x+2)}=\dfrac{x}{x-2}$.

d) $\dfrac{2}{x-y}-\left(\dfrac{x}{x-1}-\dfrac{2}{y-x}\right)-\left(\dfrac{-2}{x+y}-\dfrac{x}{x-1}\right)=\dfrac{2}{x-y}-\dfrac{x}{x-1}+\dfrac{2}{y-x}+\dfrac{2}{x+y}+\dfrac{x}{x-1} =\left(\dfrac{2}{x-y}+\dfrac{2}{y-x}\right)+\left(-\dfrac{x}{x-1}+\dfrac{x}{x-1}\right)+\dfrac{2}{x+y}=\dfrac{2}{x+y} $.

Hướng dẫn giải:

a) $x^{2}-3 x=0$

$x^2-3 x=0$ suy ra $x(x-3)=0$

TH1: $x=0$

TH2: $x-3=0 $ hay $x=3$.

b) $x^{2}-6 x+8=0$

$x^2-6 x+8=0 $

$\left(x^2-4 x\right)-(2 x-8)=0$

$(x-4)(x-2)=0$

TH1: $x-4=0 $ suy ra $x=4$

TH2: $x-2=0$ suy ra $x=2$

Vậy $x=4$ hoặc $x=2$.

Hướng dẫn giải:

1. Đổi: $100$ cm $=10$ dm.

Thể tích của hình chóp tứ giác đều đó là:

   $V=\dfrac{1}{3}.S_đ . h=\dfrac{1}{3} .30.10=100$ (dm$^3$) 

2. Xét phương trình hoành độ giao điểm của ${d}_1$ và ${d}_2$:

$ x+4=-x+4$ suy ra $ 2 x=0$ nên $ x=0 $.

Thay $x=0$ vào một trong hai hàm số của $d_1$ và $d_2$ ta tìm được $y=4$.

Vậy tọa độ giao điểm của hai đường thẳng thẳng ${d}_1$ và ${d}_2$ là $(0 ; 4)$.

Hướng dẫn giải:

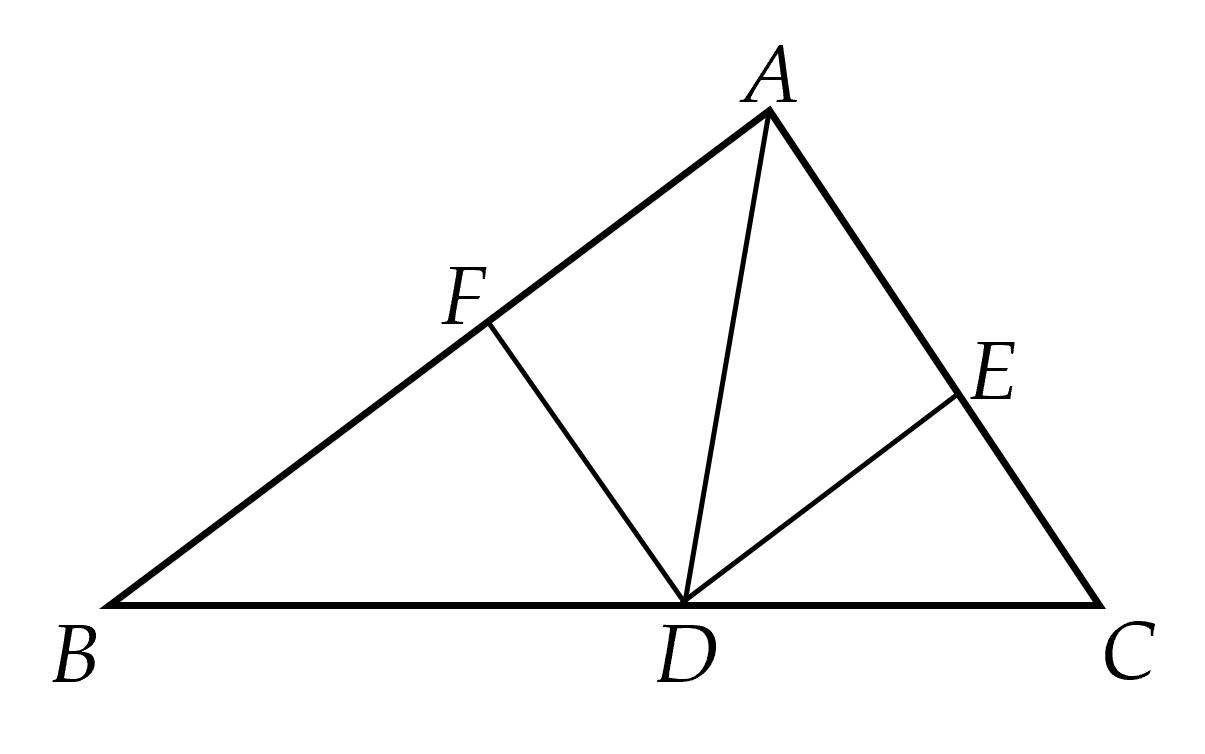
a) Xét tứ giác $A E D F$ có:

$D E$ // $A F$ (do $DE$ // $A B$);

$D F$ // $A E$ (do $D F$ // $A C)$.

Suy ra $A E D F$ là hình bình hành (DHNB)

Mà đường chéo $A D$ là tia phân giác của $\widehat{F A E}$ (gt)

Nên $A E D F$ là hình thoi (DHNB).

b) Vì $AEDF$ là hình thoi (cmt) nên $D E$ // $A F$; $DE=A F$ (tính chất)

Mà $A F=G F$ (gt) ; $G$ thuộc tia đối của tia $F A$ (gt) nên $D E=G F$; $D E$ // $D F$ 

Xét tứ giác $E F G D$ có: $D E=G F$ (cmt); $D E$ // $G F$ (cmt)

Vậy $EFGD$ là hình bình hành.

c) Theo bài ra, $G$ thuộc tia đối của tia $F A$ và $F A=F G$ suy ra $F$ là trung điểm của $A G$

Ta có: $A G=2 A F$; $I D=2 D F$

Mà $A F=D F$ (do $A E D F$ là hình thoi) suy ra $A G=I D$

Xét tứ giác $A D G I$ có:

Hai đường chéo $A G$ và $ID$ cắt nhau tại trung điểm $F$ của mỗi đường;

Suy ra $A D G I$ là hình bình hành (DHNB)

Lại có $A G=I D$ (cmt) suy ra $A D G I$ là hình chữ nhật (DHNB)

$G D$ // $I A$ suy ra $G D$ // $A K$ ($A, I, K$ thẳng hàng)

Xét tứ giác $A K D G$ có: $G D$ // $A K$ (cmt) ; $D K $ // $A G($ do $D E$ // $A F)$ 

Suy ra $A K D G$ là hình bình hành (DHNB) 

Khi đó hai đường chéo $A D$ và $GK$ cắt nhau tại trung điểm của mỗi đường 

Mà $O$ là trung điểm của $A D$ (do $O$ là giao điểm của hai đường chéo trong hình thoi $A E D F)$ 

Vậy $O$ là trung điểm của $GK$.

Hướng dẫn giải:

$x^{2}+x y+2023 x+2022 y+2023=0$

$x^{2}+x y+x+2022 x+2022 y+2022+1=0$

$x(x+y+1)+2022(x+y+1)=-1$

$(x+2022)(x+y+1)=-1 $

$x+2022=1$ hoặc $x+y+1=-1$

$x+2022=-1$ hoặc $x+y+1=1$

$x=-2021$ và $y=2019$ hoặc $x=-2023$ và $y=2023$

Vậy $(x ; y) \in\{(-2021 ; 2019) ;(-2023 ; 2023)\}$.