Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Bài 1.
1. (0,5 điểm) Không dùng máy tính cầm tay, hãy tính giá trị biểu thức:
$A=\sqrt{28}+\sqrt{63}-5\sqrt{8-2\sqrt{7}}$.
2. (1,5 điểm) Cho hai biểu thức $A=\dfrac{\sqrt{x}}{\sqrt{x}+2}$ và $B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}+2}-\dfrac{1}{2-\sqrt{x}}$ với $x \ge 0, x \ne 4$.
a) Tính giá trị của biểu thức $A$ khi $x=25$.
b) Chứng minh $B=\dfrac{\sqrt{x}}{\sqrt{x}-2}$.
c) Đặt $P=A:B$. Tìm giá trị nguyên nhỏ nhất của $x$ để $\sqrt{P}<\dfrac{1}{2}$.
Hướng dẫn giải:
1.
$A=\sqrt{2^2.7}+\sqrt{3^2.7}-5\sqrt{(\sqrt{7}-1)^2}$
$=2\sqrt{7}+3\sqrt{7}-5\left| \sqrt{7}-1 \right|$
$=2\sqrt{7}+3\sqrt{7}-5(\sqrt{7}-1 )$
$=5$.
2. a) Thay $x=25$ (thỏa mãn điều kiện) vào biểu thức $A$ ta được $A=\dfrac{\sqrt{25}}{\sqrt{25}+2}=\dfrac{5}{7}$
b) Ta có:
$B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}+2}-\dfrac{1}{2-\sqrt{x}}$
$B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}$
$B=\dfrac{x}{x-4}+\dfrac{\sqrt{x}-2}{x-4}+\dfrac{\sqrt{x}+2}{x-4}$
$B=\dfrac{x+\sqrt{x}-2+\sqrt{x}+2}{x-4}$
$B=\dfrac{x+2\sqrt{x}}{x-4}$
$B=\dfrac{\sqrt{x}(\sqrt{x}+2 )}{(\sqrt{x}-2 )(\sqrt{x}+2 )}$
$B=\dfrac{\sqrt{x}}{\sqrt{x}-2}$ (đpcm)
c) Ta có $P=A:B=\dfrac{\sqrt{x}}{\sqrt{x}+2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}$.
Để $\sqrt{P}<\dfrac{1}{2}\Rightarrow 0\le P<\dfrac{1}{4}$
+ Với $P\ge 0\Rightarrow \dfrac{\sqrt{x}-2}{\sqrt{x}+2}\ge 0\Rightarrow \sqrt{x}-2\ge 0\Rightarrow x>4$ (vì $\sqrt{x}+2>0$ với mọi $x\ge 0, x\ne 4$) $(1 )$
+ Với $P<\dfrac{1}{4}\Rightarrow \dfrac{\sqrt{x}-2}{\sqrt{x}+2}-\dfrac{1}{4}<0$
$\Rightarrow \dfrac{3\sqrt{x}-10}{4(\sqrt{x}+2 )}<0$
$\Rightarrow 3\sqrt{x}-10<0\Rightarrow \sqrt{x}<\dfrac{10}{3}\Rightarrow 0\le x<\dfrac{100}{9}$
( vì $4(\sqrt{x}+2 )>0$) $(2)$
Từ $(1 ), (2) \Rightarrow 4<x<\dfrac{100}{9}$. Mà $x$ nhận giá trị nguyên nhỏ nhất nên $x=5$.
Bài 2. (1 điểm)
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Anh Bình đến siêu thị để mua một cái bàn là và một cái quạt điện với tổng số tiền theo giá niêm yết là $850$ nghìn đồng. Tuy nhiên, thực tế khi trả tiền, nhờ siêu thị khuyến mãi để tri ân khách hàng nên giá của bàn là và quạt điện đã lần lượt giảm bớt $10\%$ và $20\%$ so với giá niêm yết. Do đó, anh Bình đã trả ít hơn $125$ nghìn đồng khi mua hai sản phẩm trên. Hỏi số tiền phải trả thực tế của từng loại sản phẩm mà anh Bình đã mua là bao nhiêu?
Hướng dẫn giải:
Gọi số tiền theo giá niêm yết của một chiếc bàn là là: $x$ (nghìn đồng) ($0<x<850$)
Thì số tiền theo giá niêm yết của một chiếc quạt điện $850-x$ (nghìn đồng)
Số tiền được giảm của một chiếc bàn là là: $10\%x=\dfrac{1}{10}x$ (nghìn đồng)
Số tiền được giảm của một chiếc quạt điện là: $20\%(850-x )=\dfrac{1}{5}(850-x)$ (nghìn đồng)
Theo bài ra ta có phương trình:
$\dfrac{1}{10}x+\dfrac{1}{5}(850-x)=125$
Giải phương trình:
$x+1\, 700-2x=1\, 250$
$x=450$ (thỏa mãn).
Vậy số tiền phải trả thực tế của bàn là là $450$ nghìn đồng và của chiếc quạt điện là $850 - 450 = 400$ nghìn đồng.
Bài 3. (1 điểm)
Một người đứng trên ngọn hải đăng cao $100$ mét quan sát hai lần một con thuyền đang đi về phía ngọn hải đăng. Lần thứ nhất người đó nhìn thấy thuyền với góc hạ là $20^\circ $, lần thứ hai người đó nhìn thấy thuyền với góc hạ là $30^\circ $. Hỏi con thuyền đã đi được bao nhiêu mét giữa hai lần quan sát? (làm tròn đến mét)

Hướng dẫn giải:
Ta có: $\widehat{xBC}=\widehat{ACB}=20{}^\circ $, $\widehat{xBD}=\widehat{ADB}=30^\circ $
Xét $\Delta ABC$ vuông tại $A$, có $AC=\dfrac{AB}{\tan \widehat{ACB}}=\dfrac{100}{\tan 20{}^\circ }$ (m)
Xét $\Delta ABD$ vuông tại $A$, có $AD=\dfrac{AB}{\tan D}=\dfrac{100}{\tan 30^\circ }$ (m)
Ta có $CD=AC-AD=\dfrac{100}{\tan 20^\circ }-\dfrac{100}{\tan 30^\circ }\approx 102$(m)
Vậy con tàu đã đi được xấp xỉ $102$ m giữa hai lần quan sát.
Bài 4. (2,5 điểm)
Cho điểm $M$ nằm ngoài đường tròn $(O; R )$. Gọi $MA, MB$ là hai tiếp tuyến với đường tròn $(O )$ ($A$ và $B$ là hai tiếp điểm). Kẻ đường kính $AD$ của $(O )$. Gọi $H$ là giao điểm của $OM$ và $AB$, $I$ là trung điểm của $BD$.
a) Chứng minh $OHBI$ là hình chữ nhật.
b) Cho biết $OI$ cắt $MB$ tại $K$. Chứng minh $KD$ là tiếp tuyến $(O)$.
c) Giả sử $OM=2R$. Tính chu vi $\Delta AKD$ theo $R$.
Hướng dẫn giải:
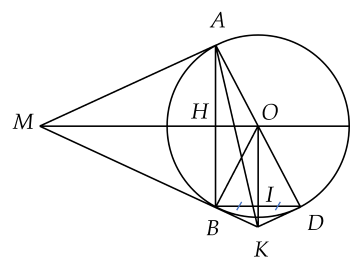
a) Xét $\Delta OBD$ cân tại $O$ (vì $OB=OD=R$) có $OI$ là đường trung tuyến nên đồng thời là đường cao.
Suy ra $OI\bot BD$(1)
Xét $\Delta OAB$ cân tại $O$ (vì $OB=OA$) có $OH$ là tia phân giác góc tại $O$ (tính chất của tiếp tuyến cắt nhau)
Nên $OH$ đồng thời là đường cao.
Suy ra $OM\bot AB$(2)
Xét tam giác $ABD$ có $OA=OB=OD$ nên $\Delta ABD$ vuông tại $B$
Suy ra $AB\bot BD$(3)
Từ (1), (2) và (3) suy ra, $OHBI$ là hình chữ nhật.
b) Xét $\Delta OBK$ và $\Delta ODK$ có:
$OB=OD\left( =R \right)$
$OK$ : cạnh chung
$\widehat{BOK}=\widehat{DOK}$ ($OI$ là tia phân giác góc $BOD$)
Do đó $\Delta OBK=\Delta ODK$ (c-g-c)
Suy ra $\widehat{ODK}=\widehat{OBK}=90^\circ $ (hai góc tương ứng)
Vậy $KD$ là tiếp tuyến của đường tròn $(O)$.
c) Xét $\Delta OMB$ vuông tại $B$ ($MB$ là tiếp tuyến của $(O)$), có:
$\sin \widehat{OMB}=\dfrac{OB}{OM}=\dfrac{R}{2R}=\dfrac{1}{2}$
Suy ra $\widehat{OMB}=30^\circ $
Vì $OHBI$ là hình chữ nhật nên $\widehat{HOI}=90^\circ $
Xét $\Delta OMK$ có $\widehat{MOK}+\widehat{OKM}+\widehat{KMO}=180^\circ $ (tổng ba góc trong một tam giác)
Suy ra $\widehat{OKM}=180^\circ -90^\circ -30^\circ =60^\circ $
Xét $\Delta OBK$ vuông tại $B$ ($MB$ là tiếp tuyến của $(O)$) có: $\tan \widehat{OKB}=\dfrac{OB}{BK}$
Suy ra $BK=\dfrac{OB}{\tan 60{}^\circ }=\dfrac{R}{\sqrt{3}}$
Ta có $BK=DK$ (hai cạnh tương ứng của hai tam giác bằng nhau)
Nên $DK=\dfrac{R}{\sqrt{3}}$
Xét $\Delta AKD$ vuông tại $D$, có
$AK^2=AD^2+DK^2$
$AK=\sqrt{4R^2+\dfrac{R^2}{3}}=\dfrac{R\sqrt{39}}{3}$
Chu vi tam giác $\Delta AKD$ là $AK+AD+KD=\dfrac{R\sqrt{39}}{3}+R+\dfrac{R\sqrt{3}}{3}=\dfrac{R}{3}\left( 3+\sqrt{39}+\sqrt{3} \right)$.
Bài 5. (0,5 điểm)
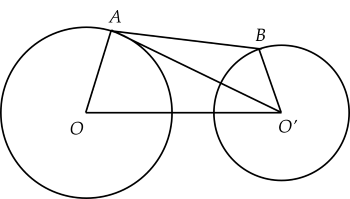
Hai hòn đảo được xem như hai hình tròn có khoảng cách từ tâm hòn đảo này đến tâm hòn đảo kia là khoảng $950$ m. Biết rằng hòn đảo lớn có bán kính khoảng $500$ m, còn đảo nhỏ có bán kính khoảng $300$ m. Người ta cần xây dựng một cây cầu bắc từ đảo này sang đảo kia. Hãy chọn vị trí để xây cầu sao cho chiều dài cây cầu là ngắn nhất, khi đó tính chiều dài cây cầu.
Hướng dẫn giải:
Gọi hòn đảo lớn là đường tròn ($O; 500$ m) và hòn đảo nhỏ là đường tròn ($O' ; 300$ m). Lấy $A$ thuộc đường tròn $(O)$ và $B$ thuộc đường tròn tâm $(O')$ là hai vị trí đầu cầu. Khi đó, $AB$ là chiều dài cây cầu và $OO' =950$ m, $OA=500$ m, $O'B=300$ m.
Xét ba điểm $O' ,A,B$, ta có $AB\ge O' A-O' B$.
Xét ba điểm $O,\,O' ,\,A$, ta có $O' A\ge OO' -OA$.
Do đó $AB\ge OO' -OA-O' B$ hay $AB\ge 150$ m.
Dấu $''=''$ xảy ra khi bốn điểm $O,\,A,\,B,\,O' $ thẳng hàng theo thứ tự đó.
Vậy ta nên đặt cầu trên đoạn nối tâm của hai đảo thì cây cầu có chiều dài ngắn nhất là $150$ m.
