Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

$A=2\sqrt{12}-\sqrt{48}+3\sqrt{27}-\sqrt{108}$

$A=2.2\sqrt{3}-4\sqrt{3}+9\sqrt{3}-6\sqrt{3}$

$A=3\sqrt{3}.$

Hướng dẫn giải:

a. Rút gọn $P.$

Điều kiện: $0<a\ne 1$

$P=\Bigg(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}} \Bigg)^2.\Bigg(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1} \Bigg)$​

$P=\Bigg(\dfrac{a-1}{2\sqrt{a}} \Bigg)^2.\Bigg(\dfrac{(\sqrt{a}-1)^2-(\sqrt{a}+1 )^2}{a-1} \Bigg)$

$P=\dfrac{{{(a-1)}^{2}}}{4a}.\dfrac{-4\sqrt{a}}{a-1}$

$P=\dfrac{1-a}{\sqrt{a}}.$

b. Tìm các giá trị của $a$ để $P<0$.

Để $P<0$ thì $\dfrac{1-a}{\sqrt{a}}<0$

khi đó $1-a<0$ (vì $\sqrt{a}>0$)

hay $a>1$ (tmđk).

Vậy $a>1$ thì $P<0.$

Hướng dẫn giải:

Gọi số công nhân và số ngày theo dự định lần lượt là $x$ (công nhân), $y$ (ngày).

Điều kiện: $x>10,\,y>2,\,x\in N$.

Lượng công việc theo dự định là $xy$ (ngày công).

Trường hợp 1: Số công nhân là $x+10$ (công nhân), số ngày là $y-2$ (ngày).

Do đó lượng công việc là $(x+10 )(y-2 )$ (ngày công).

Vì lượng công việc không đổi nên ta có phương trình

$(x+10 )(y-2 )=xy$

$-2x+10y=20\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)$

Trường hợp 2: Số công nhân là $x-10$ (công nhân), số ngày là $y+3$ (ngày).

Do đó lượng công việc là $(x-10 )(y+3 )$ (ngày công).

Vì lượng công việc không đổi nên ta có phương trình

$(x-10 )(y+3 )=xy$

hay $3x-10y=30\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)$

Từ (1) và (2) ta có hệ phương trình

$\left\{ \begin{aligned}& -2x+10y=20 \\& 3x-10y=30 \\\end{aligned} \right.$

$\left\{ \begin{aligned}& x=50 \\&y=12 \\\end{aligned} \right.$ (thỏa mãn điều kiện).

Vậy số công nhân và số ngày theo dự định lần lượt là $50$ (công nhân), $12$ (ngày).

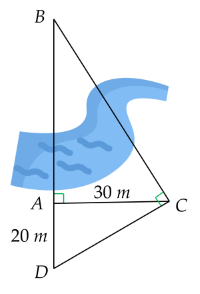
Hướng dẫn giải:

Xét tam giác vuông ADC, ta có: $\widehat{ADC}+\widehat{ACD}=90^\circ$

Xét tam giác vuông ABC, ta có: $\widehat{ACB}+\widehat{ACD}=90^\circ$

Suy ra $\widehat{ACB}=\widehat{ADC}$.

Khi đó $\tan \widehat{ACB}=\tan \widehat{ADC}$.

Hay $\dfrac{AB}{AC}=\dfrac{AC}{AD}$.

Suy ra $AB=\dfrac{AC.AC}{AD}=\dfrac{30.30}{20}=45$ (m).

Từ đó tính được $\widehat{ACB}\approx 56^\circ$.

Hướng dẫn giải:

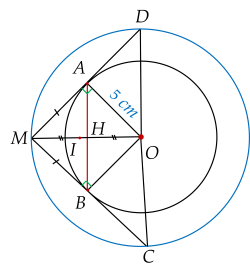
a) Gọi $I$ là trung điểm của $OM$. Xét tam giác vuông $MAO$ có $AI$ là trung tuyến nên $AI=IM=IO$ (1)

Tương tự, xét tam giác $MBO$ có $BI=IM=IO$ (2)

Từ (1) và (2), suy ra $AI=IM=IO=IB$. Vậy $A,M,B,O$ cùng thuộc đường tròn tâm $I$, bán kính $IA$.

b) Gọi $H$ là giao điểm của $OM$ và $AB$. Theo tính chất, hai tiếp tuyến cắt nhau ta có $OM$ là phân giác góc $AOB$.

Mặt khác $AOB$ là tam giác cân tại $O$, nên $OH$ cũng là đường cao, đường trung tuyến của $\Delta AOB$.

Khi đó $AH=BH=3$ cm.

Áp dụng định lí Pythagore cho tam giác vuông $AHO$, ta có:

$HO=\sqrt{AO^2-AH^2}=\sqrt{5^2-3^2}=4$ (cm).

Ta có $\sin \widehat{AOH}=\dfrac{AH}{AO}=\dfrac{3}{5}$

Suy ra $\widehat{AOB}=2\widehat{AOH} \approx 74^\circ$.

c) Ta có $\cos \widehat{AOH}=\dfrac{OH}{AO}=\dfrac{4}{5}$.

Xét tam giác vuông $MAO$, ta có:

$\cos \widehat{AOH}=\cos \widehat{AOM}=\dfrac{AO}{OM}$

Suy ra $\dfrac{AO}{OM}=\dfrac{4}{5}$, khi đó $OM=\dfrac{5OA}{4}=\dfrac{25}{4}$ (cm).

Xét tam giác cân $OMD$ có $OA$ là đường cao nên cũng là phân giác, đường trung tuyến.

Suy ra $\widehat{DOC}=4\widehat{AOM}=4\widehat{AOH} \approx 148^\circ$. Hay số đo cung nhỏ $CD$ bằng $148^\circ$.

Do đó diện tích hình quạt ứng với cung nhỏ $CD$ là:

$S_q=\dfrac{n}{360}.\pi R^2=\dfrac{148}{350}.\pi .\Big(\dfrac{25}{4} \Big)^2\approx 50$ (cm$^2$).

Hướng dẫn giải:

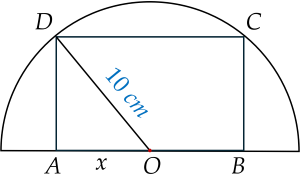
Gọi tên khu vui chơi hình chữ nhật là $ABCD$.

Đặt $OA=x$ $(0<x<10)$ (cm).

Áp dụng định lí Pythagore cho tam giác vuông $ADO$, ta có: $AD=\sqrt{10^2-x^2}$(cm).

Khi đó diện tích của khu vui chơi là:

$AD.AB=2x.\sqrt{10^2-x^2}\le x^2+10^2-x^2=100$ (cm$^2$).

Dấu “=” xảy ra, khi $x=\sqrt{10^2-x^2}$

$x^2=10^2-x^2$

$x=5\sqrt{2}$ (cm).

Vậy diện tích lớn nhất của khu vui chơi là $100$ cm$^2$ và đạt được khi hai cạnh lần lượt là $5\sqrt{2}$ cm và $10\sqrt{2}$ cm.