Bài học cùng chủ đề
Phần tự luận (7 điểm) SVIP
Bài 1 (1,5 điểm).
a) Phân tích số $270$ thành tích các thừa số nguyên tố.
b) Tìm ước chung lớn nhất rồi tìm ước chung của $180$ và $84$.
Bài 2 (1,5 điểm). Thực hiện phép tính (bằng cách hợp lí nếu có thể)
a) $85.18 + 18.16 – 18$;
b) $5^{20} : (5^{15}.6 + 5^{15}.19)$;
c) $720-\left\{ 40.\left[ \left(120-70 \right):25+2^3 \right] \right\}+2\,024^0$.
Bài 3 (1 điểm). Tìm $x$, biết:
a) $15x + 25 = 100$;
b) $4.2^x -3=125$.
Bài 4 (1 điểm). Một trường THCS có khoảng từ $400$ đến $600$ học sinh; khi xếp hàng $12$, hàng $15$, hàng $18$ đều vừa đủ hàng. Tính số học sinh của trường đó.
Bài 5 (1,5 điểm). Một mảnh vườn hình chữ nhật dài $10$ m và rộng $8$ m. Người ta làm lối đi rộng $1$ m xung quanh vườn, phần còn lại để trồng rau.
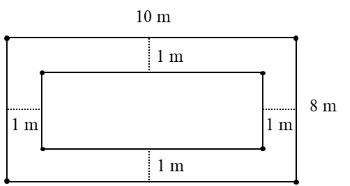
a) Tính diện tích mảnh vườn.
b) Tính diện tích phần đất để trồng rau.
c) Người ta lát toàn bộ lối đi bằng những viên gạch hình vuông có cạnh $20$ cm. Hỏi họ cần dùng bao nhiêu viên gạch như thế? (giả sử phần mạch vữa không đáng kể).
Bài 6 (0,5 điểm). Cho $A=3^{x+1}+3^{x+2}+3^{x+3}+3^{x+4}+\ldots .+3^{x+100}$ với $x \in \mathbb{N}$.
Chứng tỏ $ A$ chia hết cho $120$.