Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) Tính giá trị của biểu thức $P$ khi $x=4$.
Thay $x=4$ (thỏa mãn điêu kiện) vào biêuu thức $P$ ta có:
$P=\dfrac{4+7}{3 \sqrt{4}}=\dfrac{11}{3.2}=\dfrac{11}{6} .$

b) $Q=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{2 \sqrt{x}}{\sqrt{x}+3}+\dfrac{7 \sqrt{x}+3}{9-x}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{2 \sqrt{x}}{\sqrt{x}+3}-\dfrac{7 \sqrt{x}+3}{x-9}$

$=\dfrac{(\sqrt{x}+1)(\sqrt{x}+3)}{(\sqrt{x}-3)(\sqrt{x}+3)}+\dfrac{2 \sqrt{x}(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}+\dfrac{7 \sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}+3)}$

$=\dfrac{x+3 \sqrt{x}+\sqrt{x}+3+2 x-6 \sqrt{x}-7 \sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)}$

$=\dfrac{3 x-9 \sqrt{x}}{(\sqrt{x}-3)(\sqrt{x}+3)}=\dfrac{3 \sqrt{x}(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}=\dfrac{3 \sqrt{x}}{\sqrt{x}+3}$

c) Với $x>0 ; x \neq 9$, ta có
$A=P \cdot Q=\dfrac{x+7}{3 \sqrt{x}} \cdot \dfrac{3 \sqrt{x}}{\sqrt{x}+3}=\dfrac{x+7}{\sqrt{x}+3}=(\sqrt{x}+3)+\dfrac{16}{\sqrt{x}+3}-6$

Áp dụng bất đẳng thức Cosi cho hai số không âm ta có:

$(\sqrt{x}+3)+\dfrac{16}{\sqrt{x}+3} \geq 8 \Rightarrow(\sqrt{x}+3)+\dfrac{16}{\sqrt{x}+3}-6 \geq 2$

$\Rightarrow A \min =2$

Dấu "=" xảy ra khi và chỉ khi:

$\sqrt{x}+3=\dfrac{16}{\sqrt{x}+3} \Leftrightarrow x=1 $ (TMĐK)

Vậy giá trị nhỏ nhất của biểu thức $A=2$ tại $x=1$.

Hướng dẫn giải:

Hướng dẫn giải:

a) Xác định toạ độ hai điểm $A$ và $B$.

$(P): y=x^2 ;(d): y=3 x-2(d) \cap(P)=\{A, B\}$

Phương trình hoành độ của $({d})$ và $({P})$ là:

$x^2=3 x-2 \Leftrightarrow x^2-3 x+2=0 \Leftrightarrow\left[\begin{aligned} x=2 \\ x=1\end{aligned}\right.$

Không mất tính tổng quát ta giả sử: $x_A=2 ; x_B=1 \Rightarrow y_A=4 ; y_B=1$ Vậy ${A}(2 ; 4) ; B(1 ; 1)$.

b) Tính diện tích tam giác $O A B$. Gọi $H$ và $K$ lần lượt là hình chiếu của $B$ và $A$ trên trục $O x$.

$\Rightarrow H(1 ; 0) ; K(2 ; 0) \Rightarrow H K=\left|x_{{K}}-x_{{H}}\right|=1(d v d d)$

$S_{O A K}=\dfrac{1}{2} O K \cdot K A=\dfrac{1}{2}\left|x_K\right| \cdot\left|y_A\right|=\dfrac{1}{2} 2 \cdot 4=4(d v d t)$

$S_{O H B}=\dfrac{1}{2} O H \cdot H A=\dfrac{1}{2}\left|x_H\right| \cdot\left|y_B\right|=\dfrac{1}{2} 1 \cdot 1=\dfrac{1}{2}(d v d t)$

$S_{B H K A}=\dfrac{1}{2}(B H+K A) \cdot H K=\dfrac{1}{2}(1+4) \cdot 1=\dfrac{5}{2}(d v d t)$

$S_{O A B}=S_{O A K}-S_{O H B}-S_{B H K A}=4-\dfrac{1}{2}-\dfrac{5}{2}=1(d v d t)$

Hướng dẫn giải:

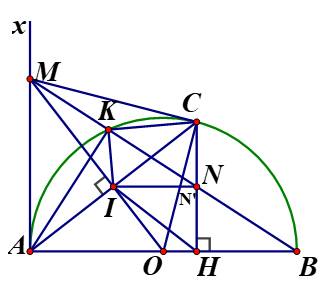
a) Xét $(O)$ có $\widehat{A K B}=90^{\circ}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \widehat{A K M}=90^{\circ}$

Có $\widehat{A I M}=90^{\circ}(\mathrm{AI} \perp M O)$

Xét tứ giác $AIKM$ có:

$\widehat{A K M}=\widehat{A I M}=90^{\circ}$

Mà $K$ và $I$ là hai đỉnh kề nhau

$\Rightarrow A I K M$ là tứ giác nội tiếp.

b) - Vì tứ giác $A I K M$ nội tiếp nên $\widehat{M I K}=\widehat{M A K}$ (Hai góc nội tiếp cùng chắn cung MK).

- Cm: $\widehat{M A K}=\widehat{A B K}$

$\Rightarrow \widehat{M I K}=\widehat{A B K}$.

- Cm tứ giác $K I O B$ nội tiếp (góc ngoài bằng góc trong tại đỉnh đối) $\Rightarrow K, I, O, B$ cùng thuộc một đường tròn.

c) - Cm $H$ là trung điểm của $A C$.

$\Rightarrow I H=I C$ (theo tính chất đường trung tuyến ứng với cạnh huyền)

$\Rightarrow \triangle I C H$ cân.

- Để $\triangle \mathrm{ICH}$ cân trở thành $\triangle I C H$ đều thì $\widehat{I C H}=60^{\circ} \Rightarrow  \widehat{M A C}=60^{\circ}$

- Tính được độ dài $A C=R \sqrt{3}$.

- Cm $M A=A C \Rightarrow$ Tìm được vị trí điểm $M$ trên tia $A x$ sao cho $A M=R \sqrt{3}$.