Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Bài 1 (1 điểm): Thực hiện phép tính
a) $\dfrac{2y-1}{y}-\dfrac{2x+1}{x}$;
b) $\dfrac{2x}{3} \, : \, \dfrac{5}{6x^2}$.
Hướng dẫn giải:
a) $\dfrac{2y-1}{y}-\dfrac{2x+1}{x}$
$=\dfrac{x(2y-1)}{xy} - \dfrac{y(2x+1)}{xy}$
$=\dfrac{2xy - x - 2xy - y}{xy} = \dfrac{-x-y}{xy}$.
b) $\dfrac{2x}{3} \, : \, \dfrac{5}{6x^2}$
$\dfrac{2x}{3} \, : \, \dfrac{5}{6x^2}=\dfrac{2x}{3}.\dfrac{6x^2}{5}$
$=\dfrac{4x^3}{5}$.
Bài 2. (2 điểm): Cho biểu thức: $P= \left(\dfrac{2x}{3x+1}-1 \right) \, : \, \left(1-\dfrac{8x^2}{9x^2-1} \right)$ với $x \ne \dfrac{1}{3}$, $x \ne -\dfrac{1}{3}$.
a) Rút gọn biểu thức $P$.
b) Tính giá trị biểu thức $P$ khi $x=2$.
Hướng dẫn giải:
a) Với $x \ne \dfrac{1}{3}$, $x \ne -\dfrac{1}{3}$. ta có:
$P= \left(\dfrac{2x}{3x+1}-1 \right) \, : \, \left(1-\dfrac{8x^2}{9x^2-1} \right)$
$= \dfrac{2x - 3x - 1}{3x+1} \, : \, \dfrac{9x^2 - 1 - 8x^2}{9x^2-1}$
$=\dfrac{-(x+1)}{3x+1}.\dfrac{9x^2-1}{x^2 - 1}$
$=\dfrac{-(x+1)}{3x+1}.\dfrac{(3x+1)(3x-1)}{(x+1)(x-1)}$
$=\dfrac{1-3x}{x-1}$.
b) Thay $x=2$ vào biểu thức ta có:
$P=\dfrac{1-3.2}{2-1}=-5$.
Bài 3. (1 điểm) Giải phương trình: $\dfrac{x+1}{3}=\dfrac{2x+5}{5}$.
Hướng dẫn giải:
$\dfrac{x+1}{3}=\dfrac{2x+5}{5}$
$\dfrac{5(x+1)}{15}=\dfrac{3(2x+5)}{15}$
$5x + 5 = 6x + 15$
$5x - 6x = 15 - 5$
$-x = 10$
$x = -10$.
Vậy phương trình có tập nghiệm $S = \left\{ -10 \right\}$.
Bài 4. (2 điểm): Cho hình vẽ
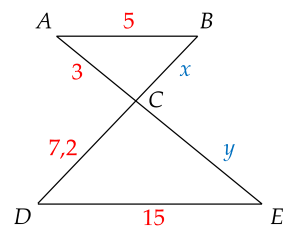
Tính độ dài $x$, $y$ biết $AB$ // $DE$.
Hướng dẫn giải:
$AB$ // $DE$.
Theo hệ quả của định lí Thalès ta có:
$\dfrac{CA}{CE}=\dfrac{CB}{CD}=\dfrac{AB}{DE}=\dfrac{5}{15}=\dfrac{1}{3}$
Hay:
⚡$\dfrac{CB}{CD}=\dfrac{1}{3}$ suy ra $\dfrac{x}{7,2}=\dfrac{1}{3}$.
Vậy $x=\dfrac{7,2 . 1}{3}=2,4 $
⚡$\dfrac{CA}{CE}=\dfrac{1}{3}$ suy ra $\dfrac{3}{y}=\dfrac{1}{3}$
Vậy $y=\dfrac{3.3}{1}=9$.
Bài 5 (1 điểm). Giải phương trình $\dfrac{2x- 50}{50}+\dfrac{2x - 51}{49}+\dfrac{2x - 52}{48}+\dfrac{2x - 53}{47}+\dfrac{2x-200}{25}=0$.
Hướng dẫn giải:
$\dfrac{2x- 50}{50} + \dfrac{2x - 51}{49} + \dfrac{2x - 52}{48} + \dfrac{2x - 53}{47} + \dfrac{2x-200}{25}=0 $
$\dfrac{2x- 50}{50} + \dfrac{2x - 51}{49} + \dfrac{2x - 52}{48} + \dfrac{2x - 53}{47}+\dfrac{2x-100}{25}+\dfrac{-100}{25}=0$
$\dfrac{2x- 50}{50}+\dfrac{2x - 51}{49}+\dfrac{2x - 52}{48}+\dfrac{2x - 53}{47}+\dfrac{2x-100}{25}+(-4)=0$
$\dfrac{2x- 50}{50}-1+\dfrac{2x - 51}{49}-1+\dfrac{2x - 52}{48}-1+\dfrac{2x - 53}{47}-1+\dfrac{2x-100}{25}=0$
$\dfrac{2x-100}{50}+\dfrac{2x - 100}{49}+\dfrac{2x - 100}{48}+\dfrac{2x - 100}{47}+\dfrac{2x-100}{25}=0$
$(2x-100).(\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+\dfrac{1}{47}+\dfrac{1}{25})=0$
$2x-100=0$ (Do $\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+\dfrac{1}{47}+\dfrac{1}{25}\ne 0$)
$x=50$.
Vậy phương trình đã cho có nghiệm $x = 50$.
