Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Câu 13. (2 điểm) Cho biểu thức $P=\dfrac{10x}{{{x}^{2}}+3x-4}-\dfrac{2x-3}{x+4}+\dfrac{x+1}{1-x}$.
a) Rút gọn $P$.
b) Tính giá trị của $P$ khi $x=-1$.
Hướng dẫn giải:
a) ĐK: ${{x}^{2}}+3x-4\ne 0$; $x+4\ne 0$ và $1-x\ne 0$ hay $x\ne 1$; $x\ne -4$.
$P=\dfrac{10x}{{{x}^{2}}+3x-4}-\dfrac{2x-3}{x+4}+\dfrac{x+1}{1-x}$
$=\dfrac{10x}{(x-1)(x+4)}-\dfrac{2x-3}{x+4}-\dfrac{x+1}{x-1}$
$=\dfrac{10x-(2x-3)(x-1)-(x+1)(x+4)}{(x-1)(x+4)}$
$=\dfrac{10x-2{{x}^{2}}+2x+3x-3-{{x}^{2}}-4x-x-4}{(x-1)(x+4)}$
$=\dfrac{-3{{x}^{2}}+10x-7}{(x-1)(x+4)}$
$=\dfrac{-(x-1)(3x-7)}{(x-1)(x+4)}$
$=\dfrac{-3x+7}{x+4}$.
Vậy $P=\dfrac{-3x+7}{x+4}$ với $x\ne 1; \, x\ne -4$.
b) Ta có: $P=\dfrac{-3x+7}{x+4}$ với $x\ne 1; \, x\ne -4$.
Khi $x=-1$ (thỏa mãn điều kiện) thì $P=\dfrac{-3.(-1)+7}{-1+4}=\dfrac{10}{3}$.
Vậy khi $x=-1$ thì $P=\dfrac{10}{3}$.
Câu 14: (1 điểm) Phân tích đa thức sau thành nhân tử
a) ${{x}^{2}}+25-10x$;
b) $-8{{y}^{3}}+{{x}^{3}}$.
Hướng dẫn giải:
a) ${{x}^{2}}+25-10x={{x}^{2}}-2.5.x+{{5}^{2}}={{\left( x-5 \right)}^{2}}$
b) $-8{{y}^{3}}+{{x}^{3}}={{x}^{3}}-{{\left( 2y \right)}^{3}}=\left( x-2y \right)\left( {{x}^{2}}+2xy+4{{y}^{2}} \right)$.
Câu 15. (2 điểm) Cho tam giác $ABC$ cân tại $A$ có đường trung tuyến $AM$, gọi $I$ là trung điểm của $AC$. Lấy điểm $K$ sao cho $I$ là trung điểm của đoạn thẳng $MK$.
a) Chứng minh tứ giác $AMCK$ là hình chữ nhật
b) Tứ giác $AKMB$ là hình gì? Vì sao?
Hướng dẫn giải:
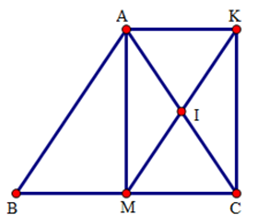
$\Delta ABC$ cân tại $A$ có $AM$ là đường trung tuyến nên $AM$ là đường cao
Suy ra $\widehat{AMC}=90^\circ$.
Xét tứ giác $AMCK$ có:
$I$ là trung điểm $AC$ (gt)
$I$ là trung điểm $MK$ ($K $ là điểm đối xứng với $M$ qua $I$).
Do đó $AMCK$ là hình bình hành.
Lại có $\widehat{AMC}=90^\circ$ suy ra $AMCK$ là hình chữ nhật.
Ta có: $AK$ // $MC$ ($AKCM$ là hình chữ nhật), $B\in MC$.
Suy ra $AK$ // $BM$ (1)
Mà $AK = MC$ ($AKCM $là hình chữ nhật), $BM = MC$ ($M$ là trung điểm của $AC$).
Suy ra $AK = BM$ (2)
Từ (1) và (2) ta có $AKMB$ là hình bình hành.
Câu 16. (1 điểm) Cho $x+y=4$ và $xy=3$. Tính ${{x}^{3}}+{{y}^{3}}$.
Hướng dẫn giải:
${{x}^{3}}+{{y}^{3}}=\left( x+y \right)\left( {{x}^{2}}-xy+{{y}^{2}} \right)=\left( x+y \right)\left( {{x}^{2}}+2xy+{{y}^{2}}-3xy \right)$
$=\left( x+y \right)\left[ \left( {{x}^{2}}+2xy+{{y}^{2}} \right)-3xy \right]=\left( x+y \right)\left[ {{(x+y)}^{2}}-3xy \right]$.
Với $x+y=4$ và $xy=3$ ta có ${{x}^{3}}+{{y}^{3}}=4\left( {{4}^{2}}-3.3 \right)=28$.
Câu 17. (1 điểm) Cho bảng số liệu sau:
|
Học sinh |
Dũng |
Bách |
Trọng |
Đô |
Ninh |
Hằng |
Anh |
|
Chiều cao (cm) |
148 |
127 |
155 |
112 |
115 |
120 |
124 |
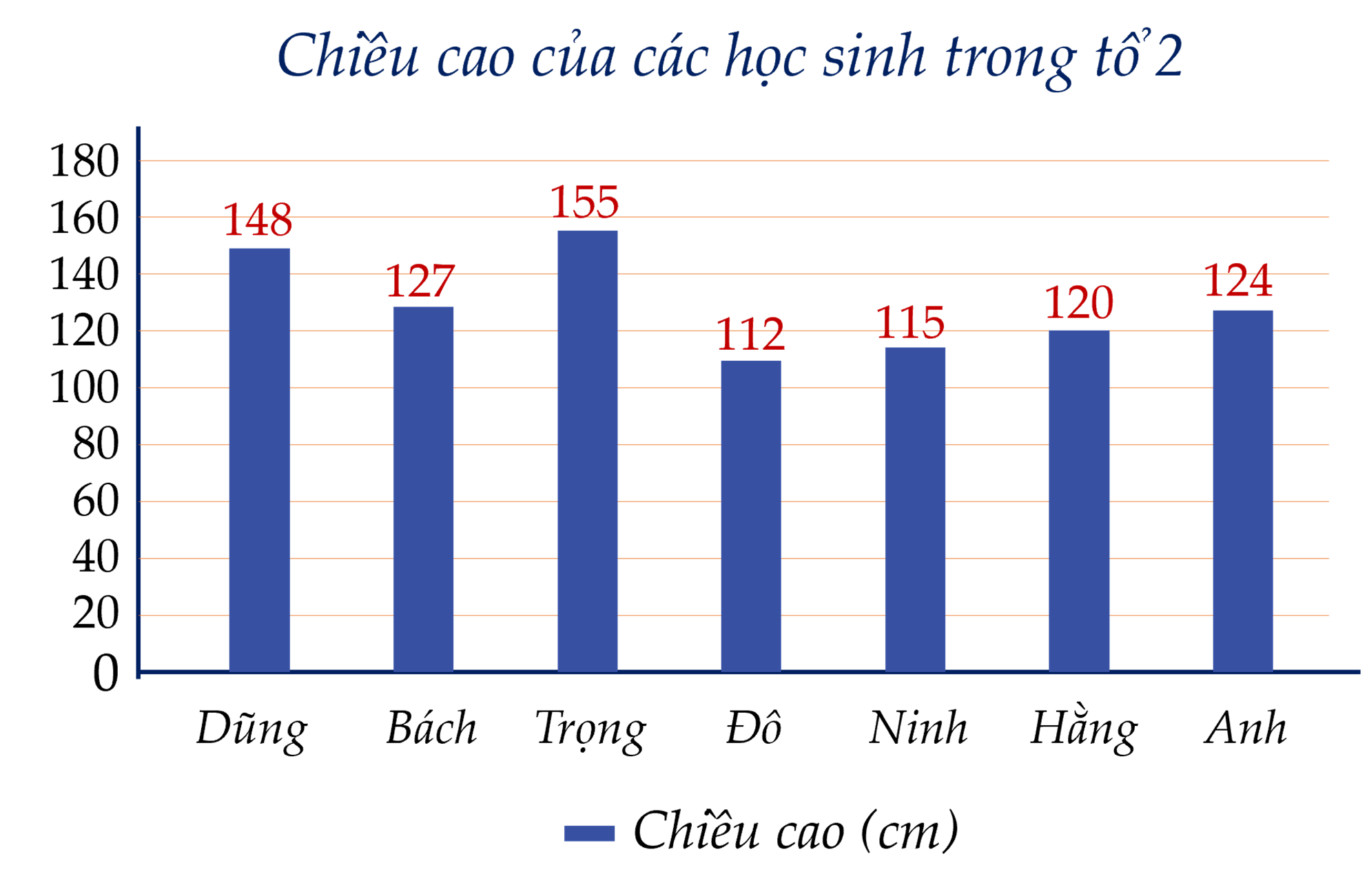
Lựa chọn biểu đồ phù hợp biểu diễn bảng thông kê này. Vẽ biểu đồ đó.
Hướng dẫn giải:
Ta lựa chọn biểu đồ cột.
Vẽ biểu đồ: