Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Câu 13. (1 điểm) Khai triển mỗi hằng đẳng thức sau.
a) ${{\left( 2x+1 \right)}^{2}}$;
b) ${{\left( a-\dfrac{b}{2} \right)}^{3}}$.
Hướng dẫn giải:
a) ${{\left( 2x+1 \right)}^{2}}=4{{x}^{2}}+4x+1$.
b) $\left( a-\dfrac{b}{2} \right)^3=a^3-3a^2.\dfrac{b}{2}+3a\left( \dfrac{b}{2} \right)^2-\left( \dfrac{b}{2} \right)^3$
$={{a}^{3}}-\dfrac{3}{2}{{a}^{2}}b+\dfrac{3}{4}a{{b}^{2}}-\dfrac{1}{8}{{b}^{3}} $.
Câu 14: (1 điểm) Phân tích đa thức sau thành nhân tử
a) ${{x}^{2}}+25-10x$;
b) $-8{{y}^{3}}+{{x}^{3}}$.
Hướng dẫn giải:
a) ${{x}^{2}}+25-10x={{x}^{2}}-2.5.x+{{5}^{2}}={{\left( x-5 \right)}^{2}}$
b) $-8{{y}^{3}}+{{x}^{3}}={{x}^{3}}-{{\left( 2y \right)}^{3}}=\left( x-2y \right)\left( {{x}^{2}}+2xy+4{{y}^{2}} \right)$.
Câu 15. (1 điểm) Tìm $x$, biết:
a) $3x\left( x-1 \right)-1+x=0$;
b) ${{x}^{2}}-9x=0$.
Hướng dẫn giải:
a) $3x\left( x-1 \right)-1+x=0$
$3x\left( x-1 \right)+\left( x-1 \right)=0$
$\left( 3x+1 \right)\left( x-1 \right)=0$
Suy ra $3x+1=0$ hoặc $x-1=0$
Vậy $x=-\dfrac{1}{3}$ hoặc $x=1$
b) $x^2-9x=0$
$x\left( x-9 \right)=0$
Suy ra $x=0$ hoặc $x=9$.
Câu 16. (2 điểm) Cho hình thang $ABCD$ ($AB$ // $CD$) có $AB=4$ cm, $CD=6$ cm. Đường thẳng $d$ song song với hai đáy và cắt hai cạnh bên $AD$, $BC$ của hình thang đó lần lượt tại $M$, $N$; cắt đường chéo $AC$ tại $P$.
a) Chứng minh $\dfrac{AM}{MD}=\dfrac{BN}{NC}$ .
b) Tính độ dài các đoạn thẳng $MP$, $PN$, $MN$; biết $MD=2MA$.
Hướng dẫn giải:
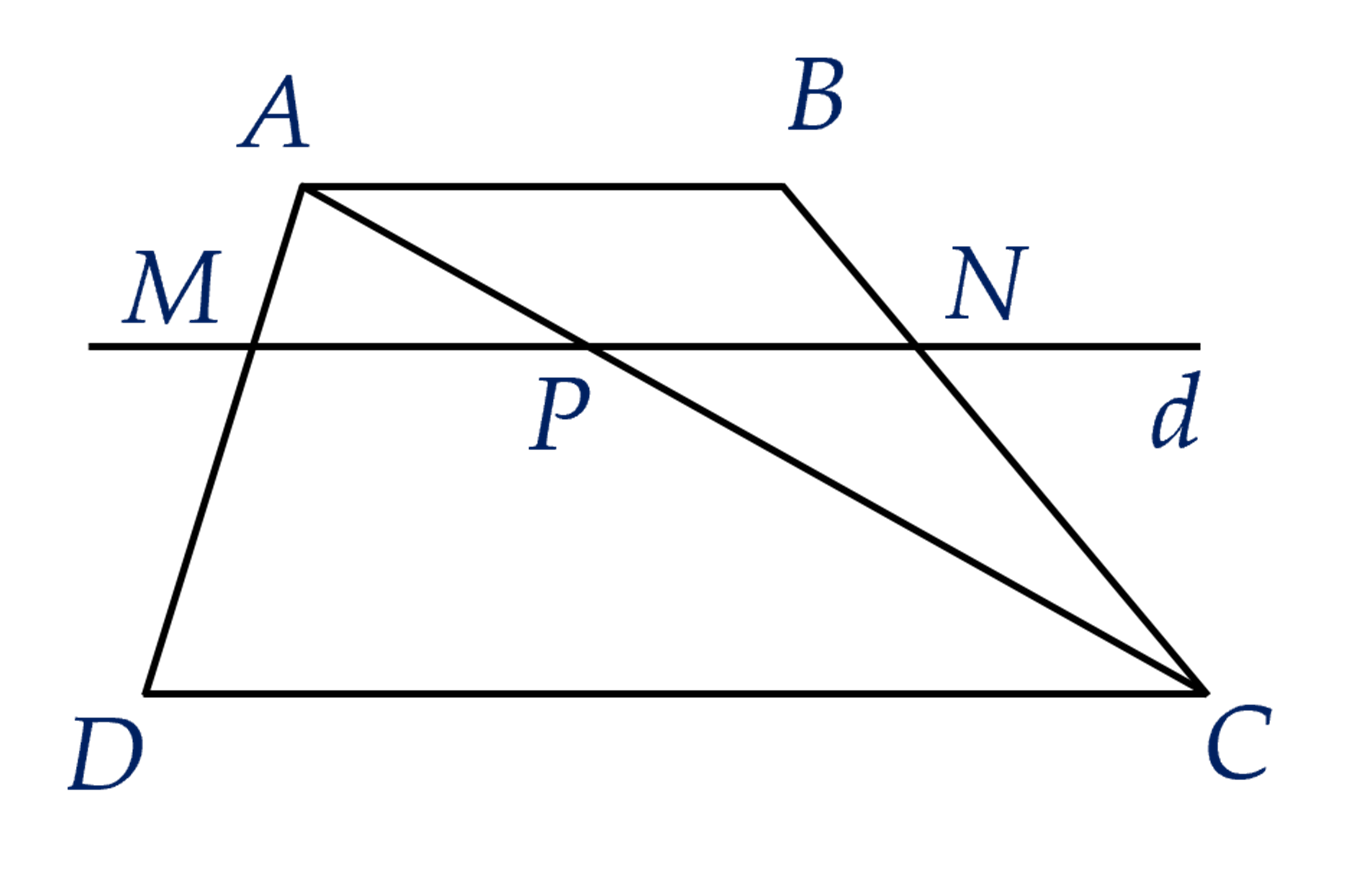
a) Vì $d $ // $CD$ // $AB$ nên $MP$ // $CD$ và $PN$ // $AB$.
Xét $\Delta ADC$ có $MP$ // $CD$:
$\dfrac{AM}{MD}=\dfrac{AP}{PC}$( Định lí Thalès) (1)
Xét $\Delta ACB$ có $NP$ // $AB$:
$\dfrac{AP}{PC}=\dfrac{BN}{NC}$( Định lí Thalès) (2)
Từ (1), (2) suy ra $\dfrac{AM}{MD}=\dfrac{BN}{NC}$
b) Chứng minh $\dfrac{MP}{DC}=\dfrac{1}{3}$
Suy ra $MP= 2$ cm
Chứng minh $\dfrac{NP}{AB}=\dfrac{2}{3}$.
Suy ra $PN=\dfrac{8}{3}$ cm.
Tính được $MN=\dfrac{14}{3}$ cm.
Câu 17. (1 điểm) Cho bảng số liệu sau:
|
Học sinh |
Dũng |
Bách |
Trọng |
Đô |
Ninh |
Hằng |
Anh |
|
Chiều cao (cm) |
148 |
127 |
155 |
112 |
115 |
120 |
124 |
Lựa chọn biểu đồ phù hợp biểu diễn bảng thông kê này. Vẽ biểu đồ đó.
Hướng dẫn giải:
Ta lựa chọn biểu đồ cột.
Vẽ biểu đồ:
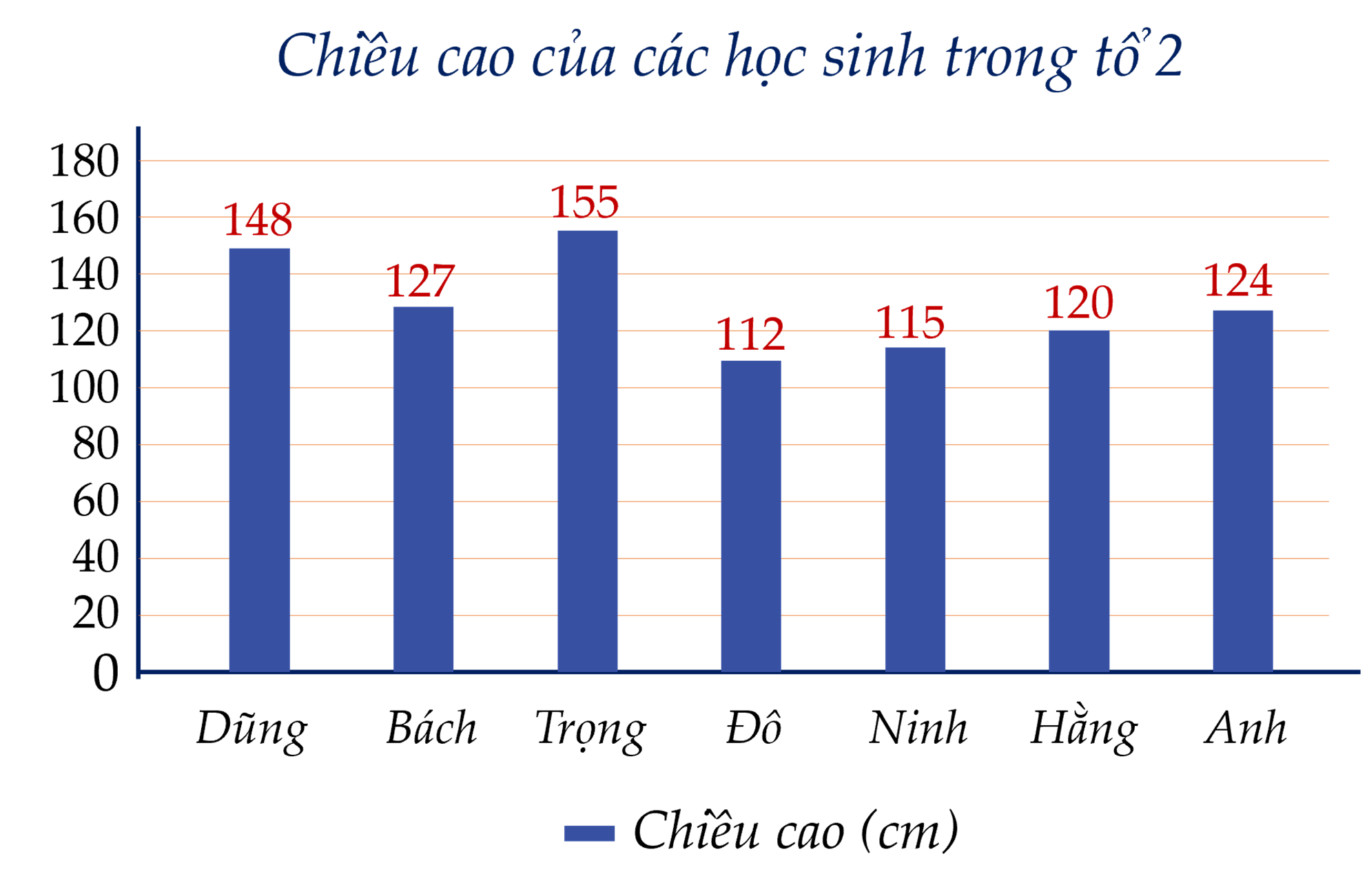
Câu 18. (1 điểm) Tìm giá trị nhỏ nhất của biểu thức $A={{x}^{2}}+2{{y}^{2}}-2xy+2x-6y+2\,028$.
Hướng dẫn giải:
Ta có: $A={{x}^{2}}+2{{y}^{2}}2xy+2x6y+2\,\,028$
$={{x}^{2}}2xy+{{y}^{2}}+{{y}^{2}}+2x-2y-4y+1+4+2\,\,023 $
$=\left[ {{x}^{2}}-2xy+\left( -{{y}^{2}} \right)+2x-2y+1 \right]+\left( {{y}^{2}}-4y+4 \right)+2\,\,023$
$={{\left( x-y+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+2\,\,023$
Vì ${{\left( x-y+1 \right)}^{2}}\ge 0$ với mọi $x, \, y$ và ${{\left( y-2 \right)}^{2}}\ge 0$ với mọi $y$.
Suy ra $A\ge 2\,\,023$.
Vậy giá trị nhỏ nhất của $A$ là $2$ $023$ đạt được khi $x-y=-1$ và $y-2=0$ hay $x=1$ và $y=2$.
