Phần tự luận SVIP

Hướng dẫn giải:

Ta có $\underset{ x\to -2}{\mathop{\lim}} \dfrac{x-1+\sqrt{2 x^2+1}}{4-x^2}=\underset{ x\to -2}{\mathop{\lim}} \dfrac{\left(x-1+\sqrt{2 x^2+1}\right)\left(x-1-\sqrt{2 x^2+1}\right)}{\left(4-x^2\right)\left(x-1-\sqrt{2 x^2+1}\right)}$

$=\underset{ x\to -2}{\mathop{\lim}} \dfrac{(x-1)^2-\left(2 x^2+1\right)}{\left(4-x^2\right)\left(x-1-\sqrt{2 x^2+1}\right)}$

$=\underset{ x\to -2}{\mathop{\lim}} \dfrac{-x^2-2 x}{\left(4-x^2\right)\left(x-1-\sqrt{2 x^2+1}\right)}$

$=\underset{ x\to -2}{\mathop{\lim}} \dfrac{-x(x+2)}{(2-x)(2+x)\left(x-1-\sqrt{2 x^2+1}\right)}$

$=\underset{ x\to -2}{\mathop{\lim}} \dfrac{-x}{(2-x)\left(x-1-\sqrt{2 x^2+1}\right)}=\dfrac{2}{-24}=\dfrac{-1}{12}$.

Vậy $\underset{ x\to -2}{\mathop{\lim}} \dfrac{x-1+\sqrt{2 x^2+1}}{4-x^2}=\dfrac{-1}{12}$.

Hướng dẫn giải:

a) $f'(x)=(x . \sin 2 x)'+(\cos x)'=x' . \sin 2 x+x. (\sin 2 x)'-\sin x=\sin 2 x+2 x . \cos 2 x-\sin x$.

b) Ta có: $f'(x)=3 x^2-3$

Tiếp tuyến có hệ số góc bằng $9$ nên $f'(x_0) = 9$

$\Leftrightarrow 3x_0^2 - 3 = 9 \Leftrightarrow \left[\begin{aligned}&x_0 = 2\\&x_0 = -2\\ \end{aligned}\right.$

Vì hoành độ tiếp điểm dương nên $x_0=2 \Rightarrow y=2$.

Tiếp tuyến cần tìm là: $y=9 x-16$.

Hướng dẫn giải:

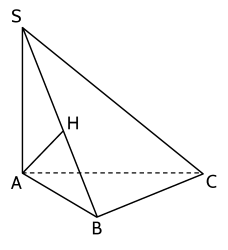
a) Ta có: $\triangle A B C$ vuông tại $B$ nên $B C \perp A B$. (1)

$S A \perp(A B C)$ nên $B C \perp S A$ (2)

Từ (1) và (2), suy ra $B C \perp(S A B)$.

b) Ta có: $B C \perp(S A B)$ suy ra $A H \perp B C$.

Mặt khác, $A H \perp S B$ nên $A H \perp(S B C) \Rightarrow A H \perp S C$.

c) Vì $\left\{\begin{aligned}&A H \perp(S B C) \\ &A H \subset(A H C)\\ \end{aligned} \Rightarrow (S B C) \perp(A H C)\right.$.

d) Vì $S A \perp(A B C)$ nên $\widehat{(S B,(A B C))}=\widehat{S B A}$.

Xét $\triangle S A B$ vuông tại $A$ có $\tan \widehat{S B A}=\dfrac{S A}{A B}=\sqrt{3} \Rightarrow  \widehat{S B A}=60^{\circ}$.

e) Theo ý b, ta có $A H \perp(S B C) \Rightarrow d_{(A,(S B C))}=A H=\sqrt{\dfrac{A B^2 . S A^2}{A B^2+S A^2}}=\dfrac{\sqrt{3} a}{2}$.