[Lý thuyết] Đánh giá độ phức tạp thời gian của thuật toán SVIP

1. Đánh giá thời gian thực hiện của chương trình

Đánh giá thời gian thực hiện của chương trình thực hiện bằng nhiều cách triển khai và chạy thuật toán, tuy nhiên cách tiếp cận này có một số vấn đề:

• Triển khai thuật toán không phù hợp với các chương trình phức tạp.
• Lãng phí thời gian triển khai nếu chương trình không được sử dụng.
• Thời gian chạy chương trình trên các thiết bị thông minh là khác nhau.
• Ngôn ngữ lập trình hoặc trình biên dịch có thể ảnh hưởng đến thời gian.

Khung nguyên tắc đánh giá
Thời gian thực hiện của chương trình đang xét bằng:
1. Một đơn vị thời gian: phép so sánh, logic cơ bản, tính số học, lệnh đơn,...
2. Tổng đơn vị thời gian thực hiện mỗi lần lặp: vòng for, while.
3. Đơn vị thời gian lớn nhất của các lệnh rẽ nhánh: lệnh if nhiều nhánh rẽ.

2. Phân tích độ phức tạp thời gian của thuật toán

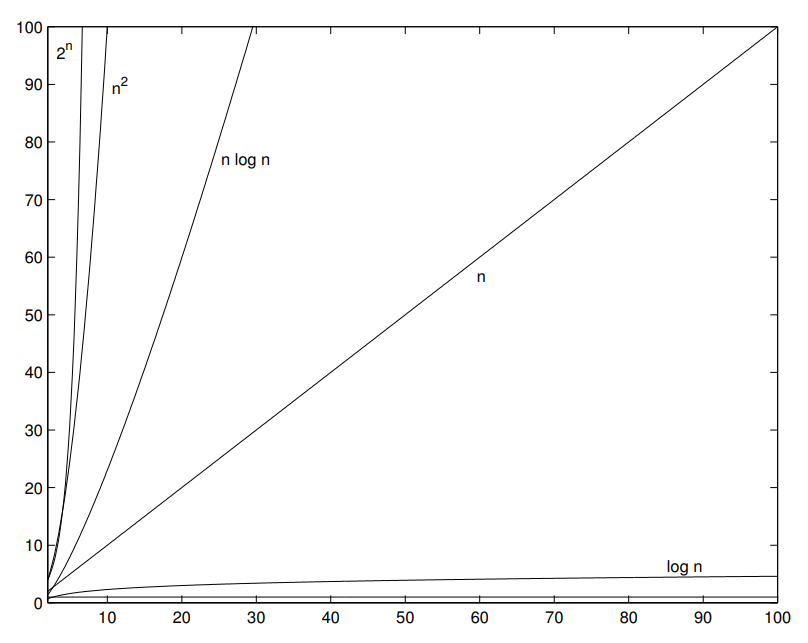
Một bài toán có thể được giải bằng nhiều thuật toán, mỗi thuật toán sẽ có hàm thời gian T(n) khác nhau. Để lựa chọn thuật toán phù hợp nhất, ta phân tích bậc của hàm T(n) khi n tăng lên vô cùng thông qua O-lớn.

❓Ví dụ:

Xác định độ phức tạp thời gian của hàm thời gian \(T\left(n\right)=n^2+3\).

Giải

Chọn \(c=2,n_0=2\). Khi đó \(n\ge n_0\), ta có:

\(T\left(n\right)=n^2+3< n^2+n_0^2\le n^2+n^2=2n^2=c.n^2\).

Vậy suy ra \(T\left(n\right)=O\left(n^2\right)\) - độ phức tạp thời gian hàm bình phương.

3. Quy tắc thực hành tính độ phức tạp thời gian của thuật toán

❓ Ví dụ: 

Hãy áp dụng quy tắc cộng cho một số hàm thời gian sau:

a) \(T\left(n\right)=10n+logn+3.\)

b) \(T\left(n\right)=5n^2+nlogn.\)

Giải

a) \(O\left(max\left(10n,logn,3\right)\right)=O\left(n\right)\)

b) \(O\left(max\left(5n^2,nlogn\right)\right)=O\left(n^2\right)\)

❓ Ví dụ: 

Hãy áp dụng quy tắc nhân cho hàm \(T\left(n\right)=10n+nlogn+3.\)

Giải

\(T\left(n\right)=10n+nlogn+3=O\left(max\left(3n^2,nlogn\right)\right)=O\left(3n^2\right)=O\left(n^2\right)\)

Tổng kết kiến thức

1. Ước lượng thời gian chạy dựa trên việc tính tổng thời gian các phép tính đơn và các lệnh đơn của chương trình.

2. O-lớn dùng để đánh giá và phân loại độ phức tạp thời gian của thuật toán khi kích thước đầu vào của bài toán tăng lên vô cùng.

3. Các thuật toán với độ phức tạp từ bậc đa thức trở xuống được gọi là các thuật toán tốt.

4. Một số quy tắc thực hành tính:

• \(O\left(f\left(n\right)+g\left(n\right)\right)=max\left(f\left(n\right),g\left(n\right)\right)\).
• \(O\left(C\cdot f\left(n\right)\right)=O\left(f\left(n\right)\right)\).
• \(O\left(f\left(n\right)\cdot g\left(n\right)\right)=O\left(f\left(n\right)\right)\cdot O\left(g\left(n\right)\right)\).