Làm quen với số thập phân vô hạn tuần hoàn SVIP

1. Số thập phân vô hạn tuần hoàn

Khi thực hiện phép chia 1 chia cho 3; 3 chia cho 11, ta có: 

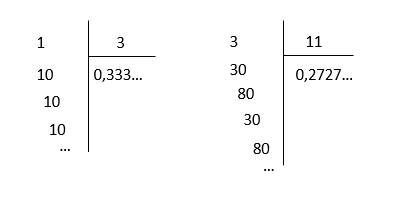
Ta nói phân số \(\dfrac{1}{3}\) được viết dưới dạng số thập phân là \(0,333...\); tương tự \(\dfrac{3}{11}=0,2727...\)

Nhận xét: trong thương của \(1\) chia cho \(3\), trong thương chữ số \(3\) được lặp mãi; trong thương của \(3\) chia cho \(11\), trong thương chữ số 27 lặp mãi.

Kết luận:

• Các số: \(0,333...;0,2727...\) là những số thập phân vô hạn tuần hoàn.
• Số \(0,333...\) viết gọn là \(0,\left(3\right)\) . Kí hiệu \(\left(3\right)\) được hiểu là chữ số \(3\) lặp lại vô hạn lần. Số \(3\) được gọi là chu kì của số thập phân vô hạn tuần hoàn \(0,\left(3\right)\). Tương tự, \(0,2727...\) có chu kì là \(27\) và được viết gọn là \(0,\left(27\right)\).
• Các số thập phân đã học như \(0,25;2,5;...\) còn được gọi là số thập phân hữu hạn.

2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước

Khi làm tròn số đến một hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.

Chú ý. Muốn làm tròn số thập phân với độ chính xác cho trước, ta có thể xác định hàng làm tròn thích hợp bằng cách sử dụng b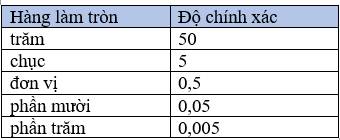ảng bên.

Ví dụ: Làm tròn số \(25891,638\) với độ chính xác:

a) \(50;\)                  b) \(0,5;\)                  c) \(0,05.\)

Giải

a)Để kết quả làm tròn có độ chính xác là \(50\), ta làm tròn đếm hàng trăm. Áp dụng quy tắc làm tròn số ta được \(25891,638\approx25900.\)

b)Để kết quả làm tròn có độ chính xác là \(0,5\), ta làm tròn đếm hàng trăm. Áp dụng quy tắc làm tròn số ta được \(25891,638\approx25891,6.\)