Tự luận SVIP

Hướng dẫn giải:

Tính được $A B=5,6 \mathrm{~km}$
Tính được vận tốc trung bình của máy bay $672 \mathrm{~km} / \mathrm{h}$.

Hướng dẫn giải:

a) \(M=\dfrac{\sin48^{\circ}}{\cos42^{\circ}}-\cos60^{\circ}+\tan27^{\circ}.\tan63^{\circ}\)

\(=\dfrac{\sin48^{\circ}}{\sin42^{\circ}}-\dfrac{1}{2}+\tan27^{\circ}.\cot27^{\circ}\)

\(=1-\dfrac{1}{2}+1=\dfrac{3}{2}\);

b) \(N=\cot27^{\circ}.\cot60^{\circ}.\cot63^{\circ}+\sin^244+\sin^246\)

\(=\cot27^{\circ}.\dfrac{\sqrt{3}}{3}.\tan27^{\circ}+\sin^244+\cos^244\)

\(=1.\dfrac{\sqrt{3}}{3}+1=1+\dfrac{\sqrt{3}}{3}\).

Hướng dẫn giải:

​​​

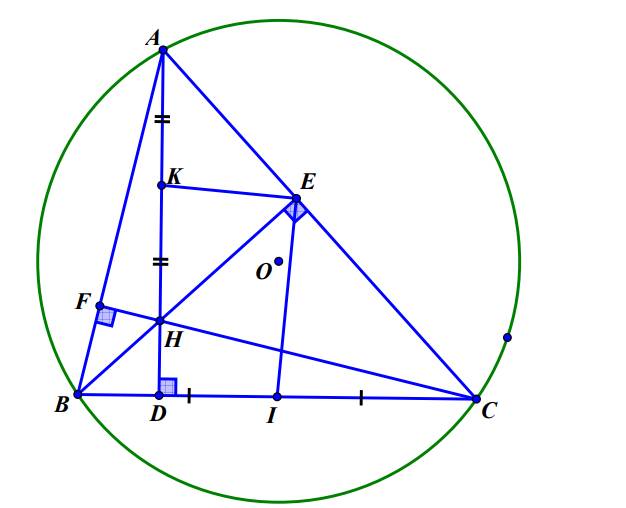
a) Hai tam giác vuông $FBC$ và $EBC$ có chung cạnh huyền, nên cùng thuộc một một đường tròn có đường kính $BC$.

b) $\triangle A B E$ đồng dạng với $\triangle A C F$ (g.g)
Suy ra : $\dfrac{A E}{A F}=\dfrac{A B}{A C}$ ,
suy ra $A B \cdot A F=A C \cdot A E$.

$EK$ là trung tuyến trong tam giác vuông $AEH$, suy ra $AKE$ và $EKH$ là tam giác cân, suy ra các yếu tố về góc bằng nhau.

$EI$ là trung tuyến trong tam giác vuông $BEC$, suy ra $BIE$ và $EIC$ là tam giác cân, suy ra các yếu tố về góc bằng nhau.
Từ đó ta chứng minh được $\widehat{KEH}$ + $\widehat{BEI}$ $= 90^{\circ}$.
Suy ra $IE \perp KE$.

c) Chứng minh được $S_{\triangle A E H} \leq O I^2$ ( $O I$ không đổi)
Suy ra: $\widehat{A C B}=45^{\circ}$.