Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Kiểm tra cuối chương I SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Hàm số y=x+35−2x nghịch biến trên khoảng nào dưới đây?
Hàm số y=x3−2x2+x+1 nghịch biến trên khoảng nào dưới đây?
Số điểm cực trị của hàm số y=34x3−2x2−x−3 là
Khẳng định nào sau đây đúng về hàm số y=x2+1?
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ:
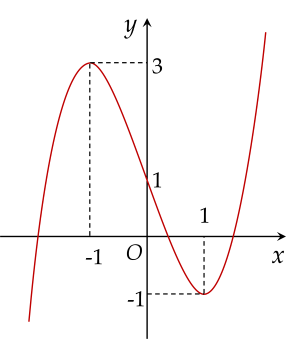
Trên đoạn [0;1], hàm số y=f(x) đạt giá trị nhỏ nhất tại
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=x+x1 trên đoạn [23;3] lần lượt là
Đồ thị hàm số y=x−15 có tiệm cận ngang là đường thẳng nào dưới đây?
Đồ thị hàm số y=x+2−3x+1 có các đường tiệm cận đứng, tiệm cận ngang lần lượt là
Biết đường thẳng y=x−2 cắt đồ thị hàm số y=x−12x+1 tại hai điểm phân biệt A và B có hoành độ xA,xB. Giá trị của biểu thức xA+xB bằng
Với giá trị nào dưới đây của m thì hàm số y=cos2x+mx đồng biến trên R?
Cho hàm số y=f(x) xác định trên R và có đồ thị hàm số y=f′(x) là đường cong như hình vẽ dưới đây.
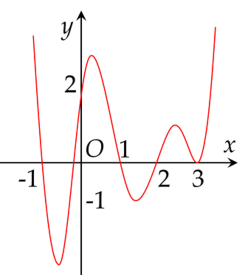
Hàm số y=f(x) có bao nhiêu điểm cực trị?
Số lượng sản phẩm bán được của một công ty trong x (tháng) được tính theo công thức S(x)=200(5−2+x9),trong đó x≥1. Xem y=S(x) là một hàm số xác định trên nửa khoảng [1;+∞), tiệm cận ngang của đồ thị hàm số đó là
Cho hàm số y=f(x)=x2+1. Số nghiệm của phương trình f(x+3)=1 là
Một cơ sở đóng giày sản xuất mỗi ngày được x đôi giày (1≤x≤20). Tổng chi phí sản xuất x đôi giày (đơn vị nghìn đồng) là C(x)=x3−6x2−88x+592. Giả sử cơ sở này bán hết sản phẩm mỗi ngày với giá 200 nghìn đồng/một đôi. Gọi T(x) là số tiền bán được và L(x) là lợi nhuận thu được sau khi bán hết x đôi giày.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Giả sử trong một ngày nào đó cơ sở sản xuất được 10 đôi giày thì lợi nhuận thu được là 1888000 (đồng). |
|
| b) Giả sử trong một ngày nào đó cơ sở lợi nhuận thu được là 1584000 đồng, khi đó cơ sở phải sản xuất được 9 đôi giày. |
|
| c) Cơ sở này sản xuất được 12 đôi giày thì lợi nhuận thu được là nhiều nhất. |
|
| d) Lợi nhuận tối đa thu được trong một ngày là 1980000 đồng. |
|
Một trang sách có dạng hình chữ nhật có diện tích 384 cm2. Sau khi để lề trên và lề dưới đều là 3 cm; lề trái và lề phải là 2 cm; phần còn lại của trang sách được in chữ. Gọi x là chiều rộng của trang sách.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Chiều dài của trang sách là: 384−x (cm). |
|
| b) Diện tích lớn nhất của trang sách được in chữ là: 360 cm2. |
|
| c) Trang sách được in chữ có diện tích lớn nhất khi x=16 (cm). |
|
| d) Phần diện tích để trống là: 144 cm2. |
|
Cho đường cong ở hình vẽ dưới là đồ thị của hàm số y=cx+dax+b với a,b,c,d là các số thực.
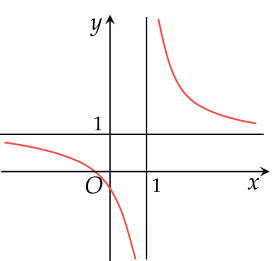
| a) Tiệm cận đứng của đồ thị hàm số là đường thẳng y=1. |
|
| b) Hàm số luôn nghịch biến trên R. |
|
| c) y′<0,∀x=1. |
|
| d) Đồ thị hàm số có một giao điểm với trục tung. |
|
Cho hàm số y=f(x)=x2−3x+2x+1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số nghịch biến trên khoảng (2;+∞). |
|
| b) Giá trị cực đại của hàm số là −5+26. |
|
| c) Điểm cực tiểu của hàm số là −5+26. |
|
| d) Hàm số nghịch biến trên khoảng (−1−6;−1+6). |
|
Một cửa hàng kinh doanh rau tươi ước tính doanh thu bởi hàm số f(x)=x2−29000x+1000100000 (đồng) và tiền lãi thu được là g(x)=1000x+100000 (đồng) với x (đồng) là giá bán cho mỗi kg rau tươi. Biết doanh thu bằng tổng tiền lãi và tiền vốn. Tìm giá bán mỗi kg rau tươi (đơn vị nghìn đồng) sao cho cửa hàng phải bỏ vốn ra ít nhất.
Trả lời:
Một chất điểm chuyển động theo quy luật và quãng đường di chuyển được sau t giây được tính theo công thức S(t)=−3t3+243t2 (m). Vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu giây?
Trả lời:
Cho y=f(x) là hàm bậc bốn và có bảng biến thiên như hình vẽ
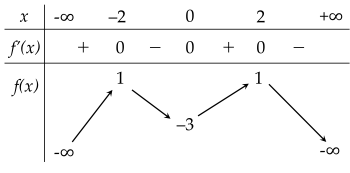
Đồ thị hàm số y=g(x)=f(x)−1(x2−4)(x−2) có bao nhiêu đường tiệm cận ngang?
Trả lời:
Cho hàm số y=f(x) liên tục trên R và có đồ thị có 3 điểm cực trị như hình dưới đây.
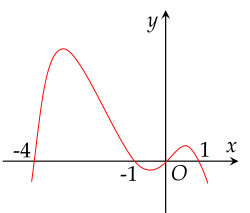
Hàm số g(x)=f(x3−3x+2) có bao nhiêu điểm cực trị?
Trả lời:
Cho hàm số y=x−12x−4 có đồ thị (C) và đường thẳng Δ:2x+y−m=0. Gọi S là tổng tất cả các giá trị của tham số m để đường thẳng Δ cắt đồ thị (C) tại hai điểm A,B phân biệt, đồng thời trung điểm của đoạn AB nằm trên đường tròn có tâm I(1;−1), bán kính R=2. Tính S (ghi kết quả dưới dạng số thập phân).
Trả lời:
