Khoảng cách giữa đường thẳng - mặt phẳng SVIP

Cho tứ diện đều $ABCD$ cạnh $a$. Khoảng cách $d$ giữa hai cạnh đối của một tứ diện đều cạnh bằng

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, $SA$ vuông góc với mặt đáy và $SA=a\sqrt{3}$. Khoảng cách giữa hai đường thẳng $SA$ và $BC$ bằng

Cho hình lăng trụ tam giác $ABC.A'B'C'$.

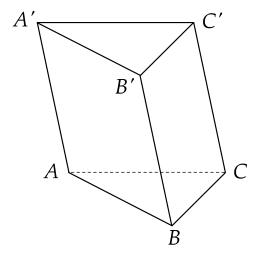
Khẳng định nào sau đây đúng?

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O$ và đường chéo $AC=a$, cạnh bên $SA$ vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng $BD$ và $SA$ bằng

Cho tứ diện $ABCD$ có $AB, \, AC, \, AD$ đôi một bằng nhau và vuông góc với nhau. $M, \, N, \, P$ lần lượt là trung điểm của $CD, \, BD, \, BC$. Khoảng cách cách giữa hai đường thẳng $AB$ và $CD$ bằng

Cho tứ diện đều $ABCD$ cạnh $a.$ Khoảng cách giữa hai đường thẳng $AB$ và $CD$ bằng

Cho hình chóp tứ giác đều $S.ABCD$. Điểm $O$ là tâm của đáy, cạnh đáy có độ dài là $2a$. Khoảng cách giữa $CB$ và $SO$ bằng

Cho hình chóp $S. A B C D$ có đáy là một hình vuông cạnh $a$, mặt bên $SAB$ là một tam giác vuông tại $A$ và $(SAB)\bot (ABCD)$. Khoảng cách giữa hai đường thẳng chéo nhau $SA$ và $BD$ bằng

Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ cạnh bằng $a$. Khoảng cách giữa $BD$ và $A{B}'$ là

Cho hình chóp $SABC$ có đáy $ABC$ là tam giác vuông cân tại $A, \, BC=4a$. Cạnh bên $SA=3a$ và vuông góc với mặt phẳng đáy $\left(ABC \right)$. Khoảng cách $d$ giữa hai đường thẳng $AB$ và $SC$ bằng