Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Hướng dẫn giải đề thi (Phần 4 - cuối) SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Cho tam giác ABC đường cao AH.
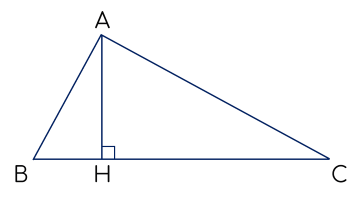
Ta có: (HB−HC)2≥0
⇔HB2+HC2≥2.HB.HC
⇔2.(HB2+HC2)≥(HB+HC)2 mà BC=HB+HC.
Khẳng định nào sau đây đúng?
HB2+HC2≥2.BC2.
HB2+HC2≤2.BC2
HB2+HC2≤21.BC2
HB2+HC2≥21.BC2.
Câu 2 (1đ):
Áp dụng bất đẳng thức Cauchy cho hai số dương 25BC2 và 2AH2 ta có bất đẳng thức nào sau đây?
25BC2+2AH2≥25.AH.BC.
25BC2+2AH2≥25.AH.BC.
25BC2+2AH2≥5.AH.BC
25BC2+2AH2≥10.AH.BC.
Câu 3 (1đ):
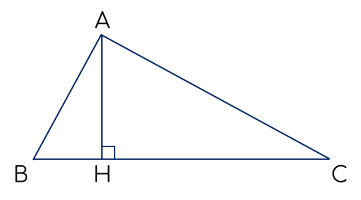
Nếu BH=HC thì ΔABC có đường cao AH là tam giác
cân tại A.
vuông tại A.
đều.
cân tại B.
Câu 4 (1đ):
Biểu thức −2x2+9x+6 bằng
−2(x2−2.x.49+1681)+1615.
(x2−2.x.49+1681)+16129.
−2(x2−2.x.49+1681)+16177.
−2(x2−2.x.49+1681)+8129.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- ý đến vị số 2 của câu 4
- số tam giác ABC có b c là các góc nhọn
- và diện tích không đổi thì khi vẽ hình
- kem chú ý cho thầy
- với tầm sắt ABC với 2 góc BC ngọn nhất
- còn trong trường hợp như thế này chẳng
- hạn thì do góc B là một góc tù hình vẽ
- này sẽ không chính xác
- và hiệu vẽ sai hình hoàn toàn có thể ảnh
- hưởng đến quá trình chứng minh Tìm giá
- trị nhỏ nhất của biểu thức này
- nên chú ý cho thầy bước vẽ hình sau đó
- thì vẽ đường cao ah h thì tam giác mà có
- chiều cao là a cạnh đáy là BC diện tích
- sẽ là 1/2 a nhân b c và chú ý diện tích
- này là không được nhá Yêu cầu tìm giá
- trị nhỏ nhất của biểu thức p
- như bạn tới đây Tiện tay vịt luôn các hệ
- thức lượng trong tam giác vuông là a
- bình bằng BH nhân BC 2 a a b bình phương
- + AC bình phương thì bằng BC bình phương
- khi phải đặc biệt cho biết cho thầy đề
- bài chưa Cho tam giác vuông á Ở đây mới
- chỉ có ah là đường cao của tam giác ABC
- là tam giác thường thôi trên hình vẽ
- chúng ta chỉ có hai tam giác vuông là
- tam giác ahb và tam giác AC với tam giác
- vuông ahb thì ta có thể sử dụng pizza ho
- lá Abe bình phương = a h bình cộng với
- BH Bình với tam giác ahc vuông tại H thì
- ta có thêm AC bình phương = a h Bình +
- ch Bình
- với tờ thấy sự tính tổng của AC Bình và
- a bình và thay vào biểu thức p ta sẽ thu
- được 2 PC Bình giữ nguyên này AC bình
- cộng b bình ta có hai a bình phương
- + về hòa bình và + ch pin
- để tìm giá trị nhỏ nhất của biểu thức
- chúng ta sẽ đưa về giả thiết liên quan
- tới diện tích không đổi tức là phải biến
- đổi biểu thức p về theo tích
- abc1 tích không đổi
- ở đây đã có mi C bình phương rồi này đã
- có ai hát này Vậy thì ta sẽ đưa ph bình
- cộng sẽ bình về theo a và b c nhất
- BH bình cộng với hc Bình tuyệt đối các
- em không đều biết thành PC tất cả bình
- với lời giải thích BH + HC = BC nhé
- BH + HC = BC bình phương hai vị taxi có
- hình thức là ph bình cộng với hai phhc
- và + ch Bình mới bằng BC Bình mà Đây
- Thấy sẽ hướng dẫn các em sử dụng một
- hình thức đã biết như sau
- HP - h c tất cả bình phương luôn lớn hơn
- hoặc bằng 0 điều này là hiển nhiên sau
- đó thì sẽ khai triển hằng đẳng thức
- Thành HP Bình - 2hp HC và + HC Bình em
- chuyển hai nhân HP nhấn HC xanh với bên
- phải như thế này ta có bất đẳng thức
- thầy sẽ + thả hai vế với đại lượng HP
- Bình + HC Bình khi vẽ trái sẽ là 2h b
- bình cộng c Bình con vì phải sẽ tạo
- thành một hằng đẳng thức chính là HP + h
- c tất cả bình phương như vậy chúng ta sẽ
- đánh giá được 2hp bình cộng với hc Bình
- sẽ lớn hơn hoặc bằng 1/2 HP + h c tất cả
- bình mà HP + h c tất cả bình thì bằng BC
- bình phương như vậy
- ta sẽ đưa biểu thức p về lớn hơn hoặc
- bằng hai bị phê bình này cộng hai a bình
- và + 1/2 BC tất cả bình phương tới đây
- BC Bình với BC Bình chúng ta nhóm lại để
- được 5 phần 2 BC bình cộng 2 a h bình
- áp dụng bất đẳng thức Cô si với các số
- dương à có tác dụng bất đẳng thức Cô si
- với hai số dương ta có a + b sẽ lớn hơn
- hoặc bằng hai ta đi Tức là lớn hơn hoặc
- bằng 2 căn 5 phần 2 nhân với căn 2 nhân
- b c nhân A
- như vậy tới đây xuất hiện BC nhân ái hát
- phát hiện số còn lại thì chính bằng 2
- căn 5
- và PC nhân a = 2 lần diện tích tam giác
- ABC nên thấy Sẽ Viết gọn biểu thức p lớn
- hơn hoặc bằng 4 căn 5 diện tích tam giác
- abc i
- A diện tích không đổi Nên giá trị nhỏ
- nhất của p sẽ là 4 căn 5 diện tích tam
- giác ABC
- bằng dấu bằng xảy ra khi nào
- game chủ yếu lại quá trình mà chúng ta
- đã đánh giá ở đây thì có hai bước đánh
- giá bước đầu tiên là dấu lớn hơn hoặc
- bằng ở đây tức là HP phải bằng HC và
- bước đánh giá thứ hai là bất đẳng thức
- Côsi
- căn 5 phần 2 PC phải bằng căn 2 hát hay
- nói cách khác ta sẽ có 2 điều kiện để
- giấu bằng xảy ra là HB = HC và BC = 29
- Cả năm chỉ là 2 căn 5 trên 5h
- tam giác ABC đường cao AH mang lại có HB
- = HC
- chính xác ta sẽ suy ra được tam giác ABC
- cân tại A bởi vì có đường cao đồng a
- trung tuyến
- phải Điều kiện thứ hai là cạnh BC sẽ
- bằng 200/5 độ dài cạnh a h Đây chỉ là
- kết quả tỷ số 2 của 4
- chuyển sang câu cuối cùng một câu vận
- dụng chiếm một điểm với yêu cầu của đề
- bài là tìm giá trị lớn nhất của biểu
- thức M với các số thực dương x y thỏa
- mãn phương trình
- ở trong phương trình này thì có xuất
- hiện các biểu thức chứa căn thây sẽ đặt
- căn y = a thì phải có điều kiện lớn
- không căn 2x + 3y = b b cũng sẽ phải lớn
- hơn không Nếu thấy bình phương hai Vậy
- thì ta sẽ có y = a bình phương và 2x + 3
- = b bình phương từ đó sẽ biểu diễn các
- đại lượng còn lại ví dụ như ý cộng một
- này hay là trừ 6 x - chí về theo a và b
- bởi vì chúng ta sẽ có những thuận lợi Ví
- dụ như - 6 - 9 em ra ngoài trong ngoặc
- sẽ còn lại 6 x cộng 9 mà 6X + chín thì
- chính là 3 b bình phương như vậy phương
- trình ban đầu này ta hoàn toàn có thể
- đưa về theo a và b là a nhân với y chính
- là a bình này + 1 - 6X + 9 là ba bình
- phương con với phải 2x cộng 4 thì lá b
- bình phương cộng 1 nhân với b và - 3A
- bình phương
- khai triển và chuyển với ta sẽ thấy xuất
- hiện các nhân tử chung đó là a mũ 3 trừ
- 10 bộ ba có nhân tử a trừ b a bình trừ b
- bình cũng có nhân tử a trừ B và ngoặc
- cuối cùng này cũng có nhân tử a trừ B ta
- sẽ đặt a trừ B ra ngoài bên trong còn
- lại hàng lấy thức thứ nhất sẽ còn a bình
- + AB + b bình đẳng thức thứ hai còn lại
- 3 a + 3 b và cuối cùng cộng với một bằng
- không trong
- các bạn sẽ quên mất cộng với một hệ số
- của a trừ B Này Nhá lên kem đặc biệt
- phải chú ý phương trình tích tay ta sẽ
- có a = b là chắc chắn rồi Còn lại hoặc
- thứ hai trong thì rất phức tạp Nhưng
- điều đầu tiên nghĩ tới là chúng ta cố
- gắng chứng minh đó là một phương trình
- vô nghiệm điều kiện chúng ta lớn không B
- lớn hơn 0 cả phần này lớn hơn hẳn không
- cộng 1 cành lớn không Rồi do đó phương
- trình tích sẽ chỉ có nhiệm a = b a = b
- hay chính là căn y = căn 2x cộng 3 bình
- phương 2x cho cả hai về đều Dương ta có
- y = 2 + 3
- thấy y = 2 + 3 và biểu thức m cần tìm
- giá trị lớn nhất ta sẽ có trừ 2 x bình +
- 9 x + 6 Đây là một tam thức bậc hai dạng
- ax bình cộng bx cộng c ti hoàn toàn kèm
- Ừ thì biến đổi và đánh giá như bài trước
- ta sẽ thêm bớt để xuất hiện hằng đẳng
- thức ở đây - 2 thì ta sẽ đặt chữ hay ra
- bên ngoài bên trong còn ít bình này - 9
- phần 2 x thấy sẽ viết thành 2 nhân với
- 9/4 và nhân với x để hoàn thành hình
- thức thì ta phải cộng với 9/4 tất cả
- bình tức là cộng với 81/16 con ở đây mới
- chỉ là -2 x 81,6 tức là âm 81/8 lên ta
- sẽ phải cộng thêm
- như vậy biểu thức mơ của chúng ta sẽ là
- - 2 nhân với x trừ 9/4 tất cả bình
- phương và cộng với
- 129/8 do phần này nhỏ hơn hoặc bằng 0
- với mọi đi động với
- 129/8 thì nhỏ hơn hoặc bằng dương 129/8
- đó chỉ là giá trị lớn nhất của biểu thức
- mờ bằng
- 129/8 dấu bằng xảy ra khi mà ít bằng 9/4
- - a Tư chứa sóng nhá kèm chú ý chúng ta
- còn y nữa thai trở lại phương trình y =
- 2 + 3 ta tìm đường y = 15/2 như vậy giá
- trị lớn nhất của biểu thức mờ là
- 129/8 đạt được khi x bằng 9/4 và y = 15
- phần 2 và túi bệnh này thì thấy Không
- tìm điều kiện xác định bởi vì người ta
- cho các số thực dương x y dẫn tới căn y2
- là thăng 2x + 3 là hoàn toàn có nghĩa
- Còn với những bài toán mà chưa cho điều
- kiện x y thì nhớ tìm đưa thầy điều kiện
- xác định trước thì làm bài nhé
- Ở trên đây là nội dung đề thi của Sở
- Giáo dục và Đào tạo Hải Dương năm 2021
- 2022
- thấy cảm ơn sự theo dõi của kem và hẹn
- gặp lại các em trong các bài học tiếp
- theo chỉ gọi lab.vn
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây