Góc và cạnh của một tam giác SVIP

1. TỔNG SỐ ĐO BA GÓC CỦA MỘT TAM GIÁC

Định lí:

Tổng số đo ba góc của một tam giác bằng $180\degree$.

Ví dụ: Tìm số đo các góc chưa biết của các tam giác trong hình vẽ dưới đây.

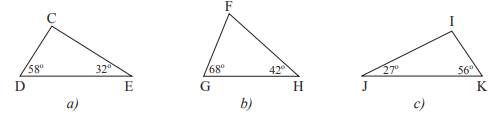
Giải

Áp dụng định lí về tổng số đo ba góc của tam giác, ta có:

a) \(\widehat{C}=180^\circ-32^\circ-58^\circ=90^\circ\).

b) \(\widehat{F}=180^\circ-68^\circ-42^\circ=70^\circ\).

c) \(\widehat{I}=180^\circ-27^\circ-56^\circ=97^\circ\).

Chú ý:

- Tam giác có 3 góc nhọn được gọi là tam giác nhọn.

- Tam giác có 1 góc vuông được gọi là tam giác vuông, cạnh đối diện góc vuông gọi là cạnh huyền, hai cạnh còn lại là hai cạnh góc vuông.

- Tam giác có 1 góc tù được gọi là tam giác tù.

Nhận xét: Trong một tam giác vuông, tổng hai góc nhọn bằng $90\degree$.

2. QUAN HỆ GIỮA BA CẠNH CỦA MỘT TAM GIÁC

Định lí:

Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.

Xét một tam giác $ABC$ bất kì, ta luôn có các bất đẳng thức sau: 

$AB+AC>BC$;

$AB+BC>AC$;

$AC+BC>AB$.

Các bất đẳng thức trên được gọi là bất đẳng thức tam giác.

Từ bất đẳng thức tam giác $AB+BC>AC$, ta suy ra:

$AB>AC-BC$;

$BC>AC-AB$.

Nhận xét: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại.

Ví dụ: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) $2$ cm; $3$ cm; $6$ cm;

b) $2$ cm; $4$ cm; $6$ cm;

c) $3$ cm; $4$ cm; $6$ cm.

Giải

Ta có:

a) $6>2+3$;

b) $6=2+3$;

$4-3<6<4+3$.

Vậy chỉ có bộ ba $3$ cm; $4$ cm; $6$ cm có thể là độ dài ba cạnh của một tam giác.

Lưu ý: Khi xét độ dài ba đoạn thẳng có thỏa mãn các bất đẳng thức tam giác hay không, ta chỉ cần so sánh độ dài lớn nhất với tổng của hai độ dài còn lại, hoặc so sánh độ dài nhỏ nhất với hiệu của hai độ dài còn lại.