Góc ở vị trí đặc biệt SVIP

I. HAI GÓC KỀ NHAU

Cho đường thẳng $xy$. Từ một điểm $O$ trên đường thẳng $xy$ ta vẽ hai tia $Oz$, $Ot$. 

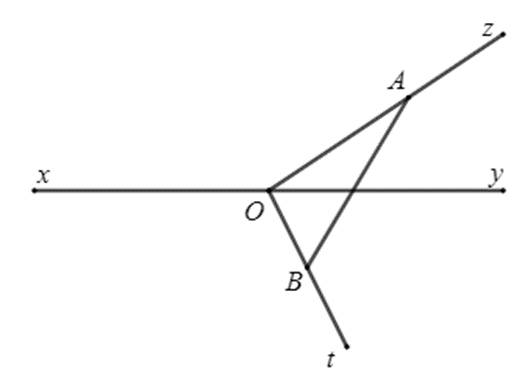
Hình 1

Lấy điểm $A$ bất kì trên tia $Oz$ ($A$ khác $O$), lấy điểm $B$ bất kì trên tia $Ot$ ($B$ khác $O$), vẽ đoạn thẳng $AB$. Ta thấy đoạn thẳng $AB$ cắt đường thẳng $xy$.

Hai tia $Oz$ và $Ot$ như vậy gọi là nằm về hai phía của đường thẳng $xy$.

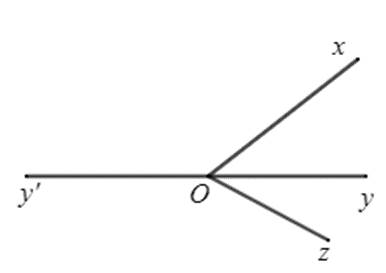
Hình 2

Hai góc $xOy$ và $zOy$ ở Hình 2 có tính chất sau: Hai góc đó có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó. Hai góc $xOy$ và $zOy$ như vậy gọi là hai góc kề nhau.

Tương tự, hai góc $zOy'$ và $xOy'$ cũng là hai góc kề nhau.

Ví dụ: Tìm các cặp góc kề nhau có trong hình vẽ sau:

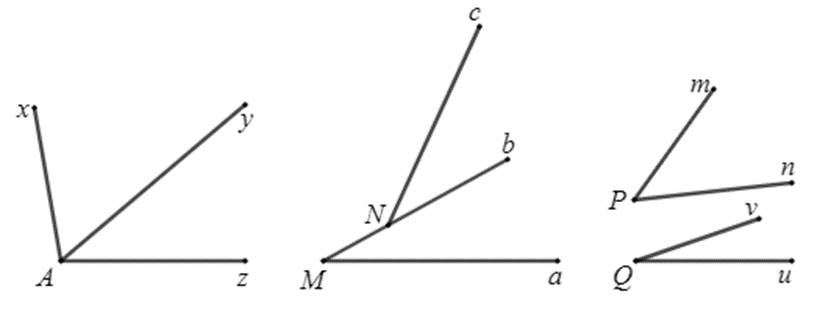
Giải

Các cặp góc kề nhau là: $xAy$ và $yAz$, $bNc$ và $cNM$.

Chú ý: Ta có tính chất sau: Cho góc $xOz$ và tia $Oy$ nằm trong góc đó, tức là mỗi điểm $M$ ($M$ khác $O$) của tia $Oy$ đều là điểm trong của góc $xOz$. Khi đó hai góc $xOy$ và $yOz$ là hai góc kề nhau và \(\widehat{xOz}=\widehat{zOy}+\widehat{yOz}\).

II. HAI GÓC BÙ NHAU. HAI GÓC KỀ BÙ

Hai góc bù nhau là hai góc có tổng số đo bằng $180\degree$.

Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.

Hai góc kề bù có tổng số đo bằng $180\degree$.

Ví dụ: Tìm hai góc kề bù trong hình vẽ sau:

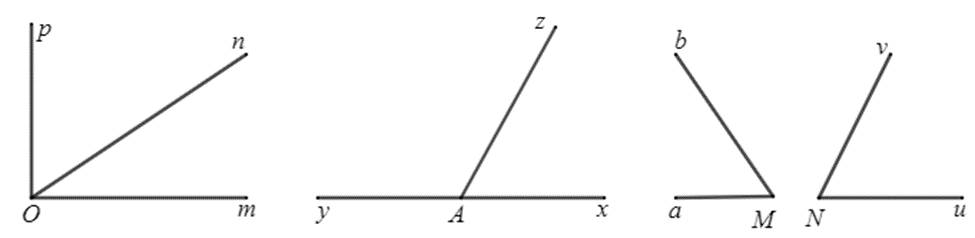
Giải

Hai góc $xAz$ và $zAy$ là hai góc kề bù.

III. HAI GÓC ĐỐI ĐỈNH

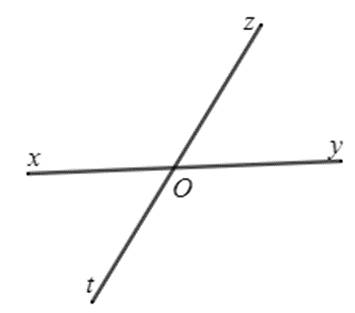
Hình 3

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Chẳng hạn, ở Hình 3, hai góc $xOz$ và $yOt$ là hai góc đối đỉnh, hai góc $yOz$ và $xOt$ cũng là hai góc đối đỉnh.

Hai góc đối đỉnh thì bằng nhau.

Ví dụ: Tìm số đo góc $yOt$ trong hình vẽ sau:

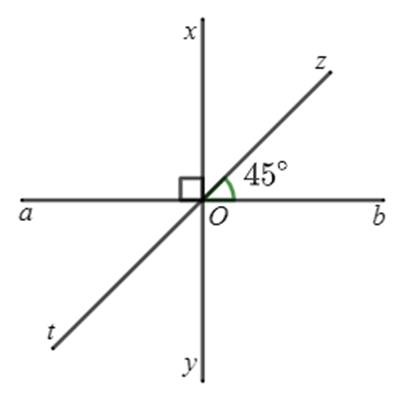
Giải

Hai góc $bOz$ và $zOx$ là hai góc kề nhau, mà \(\widehat{bOx}=90^0\) nên \(\widehat{bOz}+\widehat{zOx}=90^0\).

Vì \(\widehat{bOz}=45^0\) nên \(\widehat{zOx}=90^0-\widehat{bOz}=45^0\).

Lại có, góc $yOt$ và góc $zOx$ là hai góc đối đỉnh, suy ra \(\widehat{yOt}=\widehat{zOx}\).

Vậy \(\widehat{yOt}=45^0\).