Điểm và đường thẳng SVIP

1. ĐIỂM THUỘC, KHÔNG THUỘC ĐƯỜNG THẲNG

a. Điểm thuộc đường thẳng

Ta thường dùng chữ cái in hoa để đặt tên điểm và dùng chữ cái thường để đặt tên đường, chẳng hạn điểm $M$, đường thẳng $d$,...

Em hãy quan sát hình sau và xem các cách diễn tả dưới đây:

 + Điểm $M$ thuộc đường thẳng $d$. Kí hiệu: $M \in d$.

 + Điểm $N$ không thuộc đường thẳng $d$. Kí hiệu: $N \notin d$.

Nếu $M \in d$, ta còn nói: Điểm $M$ nằm trên đường thẳng $d$, hay đường thẳng $d$ đi qua điểm $M$.

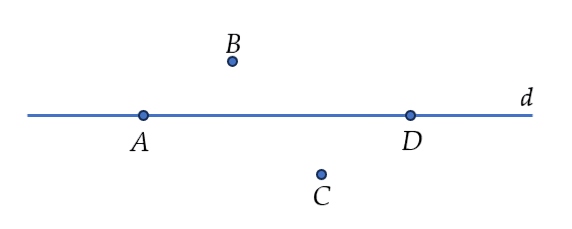
Ví dụ 1. Quan sát hình vẽ sau và cho biết, những điểm nào thuộc đường thẳng $d$, những điểm nào không thuộc đường thẳng $d$?

Lời giải

Ta có:

Điểm $A$ thuộc đường thẳng $d$. Kí hiệu: $A \in d$.

Điểm $B$ không thuộc đường thẳng $d$. Kí hiệu: $B \notin d$.

Điểm $C$ không thuộc đường thẳng $d$. Kí hiệu: $C \notin d$.

Điểm $D$ thuộc đường thẳng $d$. Kí hiệu: $D \in d$.

 b. Đường thẳng đi qua hai điểm phân biệt     

Ta thấy chỉ có thể vẽ được đúng một đường thẳng đi qua hai điểm phân biệt $A$, $B$. Đường thẳng đó được gọi là đường thẳng $AB$ hoặc đường thẳng $BA$.

Ta có nhận xét sau: Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm phân biệt.

Chú ý. Để nhấn mạnh hai phía của đường thẳng, người ta còn dùng hai chữ cái thường để đặt tên, chẳng hạn đường thẳng $xy$ như hình dưới đây.

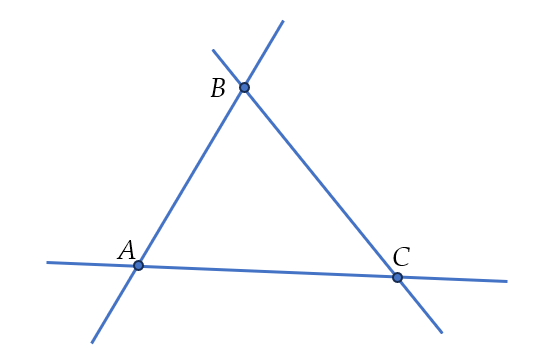
Ví dụ 2. Kể tên các đường thẳng có trong hình dưới đây. 

 Lời giải

Các đường thẳng có trong hình là: đường thẳng $AB$ (hoặc đường thẳng $BA$), đường thẳng $AC$ (hoặc đường thẳng $CA$), đường thẳng $BC$ (hoặc đường thẳng $CB$).

2. BA ĐIỂM THẲNG HÀNG

Quan sát hình vẽ và các cách biểu đạt tương ứng sau:

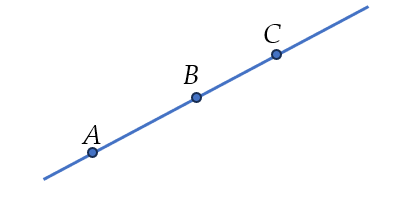
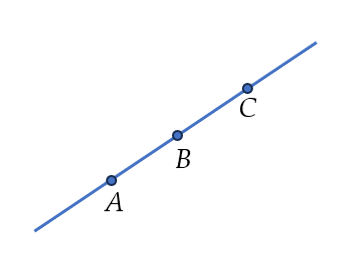
 Ba điểm $A$, $B$, $C$ thẳng hàng

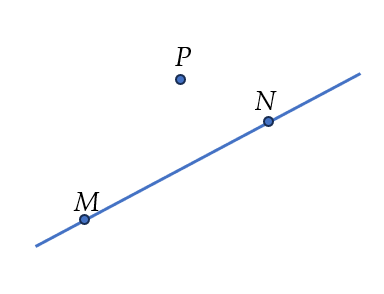
Ba điểm $M$, $N$, $P$ không thẳng hàng  

Ba điểm thẳng hàng là ba điểm cùng thuộc một đường thẳng.

Ví dụ 3. Kể tên hai bộ ba điểm thẳng hàng trong hình dưới đây. 

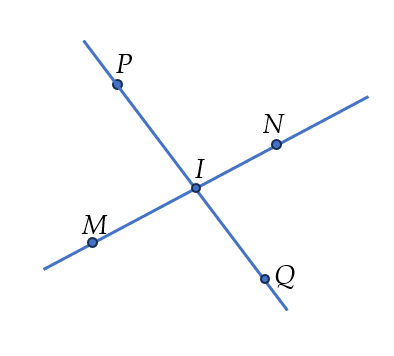
Lời giải

Ba điểm $M$, $I$, $N$ thẳng hàng vì chúng cùng nằm trên một đường thẳng.

Ba điểm $P$, $I$, $Q$ thẳng hàng vì chúng cùng nằm trên một đường thẳng.

3. HAI ĐƯỜNG THẲNG SONG SONG, CẮT NHAU, TRÙNG NHAU

1. $a$ và $b$ không có điểm chung

 $a$ và $b$ song song với nhau. Kí hiệu: $a$ // $b$. 

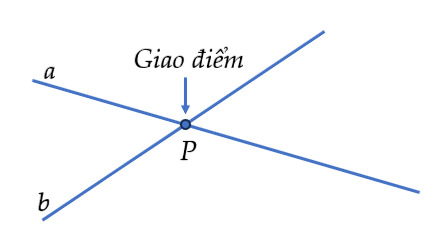
2. $a$ và $b$ có đúng một điểm chung $P$

 $a$ và $b$ cắt nhau tại $P$.

3. Đường thẳng $AB$ và đường thẳng $BC$ trùng nhau

 

Ví dụ 4. Một số hình ảnh về hai đường thẳng song song hoặc cắt nhau trong thực tế.

a) Hình ảnh hai đường thẳng song song trong thực tế.

b) Hình ảnh hai đường thẳng cắt nhau trong thực tế.