Nội dung đề thi (120 phút) SVIP

Hướng dẫn giải:

a) Thực hiện phép tính: $2 \sqrt{25}-\sqrt{16}=2.5-4=6$
b) Hai đường thẳng $\left(d_{1}\right)$ và $\left(d_{2}\right)$ cắt nhau vì $3 \neq-2$
c) $2 x-3=7 \Leftrightarrow 2 x=10 \Leftrightarrow x=5$
Vậy nghiệm của phương trình là: $x=5$
d) $\left\{\begin{array}{l}x+4 y=11 \\ x+3 y=9\end{array} \Leftrightarrow\left\{\begin{array}{l}y=2 \\ x=11-4 y\end{array} \Leftrightarrow\left\{\begin{array}{l}y=2 \\ x=11-4.2\end{array} \Leftrightarrow\left\{\begin{array}{l}x=3 \\ y=2\end{array}\right.\right.\right.\right.$
Vậy nghiệm của hệ phương trình là: $(x ; y)=(3 ; 2)$

Hướng dẫn giải:

Gọi chiều rộng của mảnh vườn nhà bạn Hoàng là: $x(m)(x>0)$
Khi đó: Chiều dài mảnh vườn nhà bạn Hoàng là: $x+6(~m)$
Vi diện tích của mảnh vườn là $216 m^{2}$ nên ta có phương trình:
$
\begin{aligned}
x(x+6)=216 \Leftrightarrow x^{2}+6 x-216=0 \\
\Delta^{\prime}=3^{2}-1 \cdot(-216)=225>0
\end{aligned}
$
$\Rightarrow$ Phương trình có hai nghiệm phân biệt:
$
\begin{aligned}
&x_{1}=\dfrac{-6+\sqrt{225}}{2.1}=12(tm) \\
&x_{2}=\dfrac{-6-\sqrt{225}}{2.1}=-18(loại)
\end{aligned}
$
Chiều dài của mảnh vườn nhả bạn Hoàng là: $12+6=18(~m)$
Vậy chiều rộng và chiều dài của mảnh vườn nhà bạn Hoàng lần lượt là $12 m$ và $18m$.

Hướng dẫn giải:

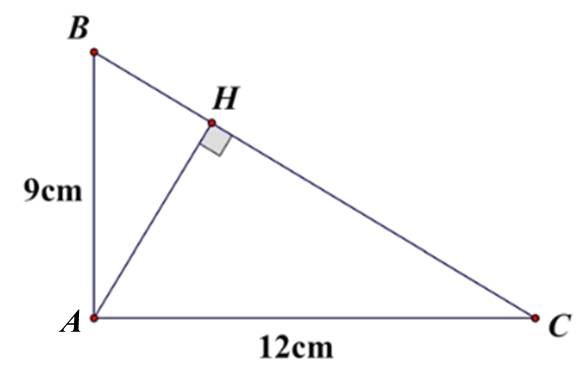
a) Xét $\triangle A B C$ vuông tại $A$ có:
$
B C^{2}=A B^{2}+A C^{2} \text { (Đinh li Py-ta-go) }
$
$
=9^{2}+12^{2}=225
$
$
\Rightarrow B C=\sqrt{225}=15(~cm)
$
Vậy $B C=15 m$
b) Xét $\triangle A B C$ vuông tại $A$, dường cao $A H$ có:
$A B \cdot A C=A H \cdot B C$ (Hệ thức lượng trong tam giác vuông)
$\Rightarrow A H=\dfrac{A B \cdot A C}{B C}=\dfrac{9.12}{15}=7,2(cm)$.

Vậy $A H=7,2 cm$.

Hướng dẫn giải:

a) Vì $B D, C E$ là đường cao của $\triangle A B C$ nên: $A E H=90^{\circ} ; A D H=90^{\circ}$
Xét tứ giác $A D H E$ có: $\widehat{A E H}+\widehat{A D H}=90^{\circ}+90^{\circ}=180^{\circ}$
$\Rightarrow$ Tứ giác $A D H E$ là tứ giác nội tiếp
b) Vì tứ giác $A D H E$ là tứ giác nội tiếp nên
$\widehat{A D E}=\widehat{A B C}$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp)
Xét $\triangle A D E$ và $\triangle A B C$ có: $\widehat{B A C}$ chung; $\widehat{A D E}=\widehat{A B C}(cmt)$
$\Rightarrow \triangle A D E \backsim \triangle A B C(g . g)$
$\Rightarrow \dfrac{D E}{B C}=\dfrac{A D}{A B}$ (Tính chất hai tam giác đồng dạng)
Xét $\triangle A B D$ có vuông tại $D$ có:
$\cos \widehat{B A D}=\dfrac{A D}{A B} \Rightarrow \dfrac{A D}{A B}=\cos 45^{\circ}=\dfrac{\sqrt{2}}{2} \Rightarrow \dfrac{D E}{B C}=\dfrac{\sqrt{2}}{2}$
Vậy $\dfrac{D E}{B C}=\dfrac{\sqrt{2}}{2}$.

Hướng dẫn giải:

Vì $m^{2}+m+1=\left(m+\dfrac{1}{2}\right)^{2}+\dfrac{3}{4} \neq 0 \forall m$ nên phương trình (1) là phương trình bậc 2 ẩn $x$ với mọi $m$
Phương trình (1) có hai nghiệm $x_{1} ; x_{2}$ khi và chỉ khi:
$\Delta \geq 0$ $\Leftrightarrow\left(m^{2}+2 m+2\right)^{2}+4\left(m^{2}+m+1\right) \geq 0$ $\left.m^{2}+m+1=\left(m+\dfrac{1}{2}\right)^{2}+\dfrac{3}{4}>0 \forall m\right)$
Áp dụng định lý Vi-ét ta có: $x_{1}+x_{2}=\dfrac{m^{2}+2 m+2}{m^{2}+m+1}$
$\Leftrightarrow S=\dfrac{m^{2}+2 m+2}{m^{2}+m+1}$
$\Leftrightarrow m^{2} S+m S+S=m^{2}+2 m+2$
$\Leftrightarrow(S-1) m^{2}+(S-2) m+S-2=0(*)$
* Nếu $S=1 \Rightarrow-m+1-2=0 \Leftrightarrow m=-1$
* Nếu $S \neq 1$, khi đó phương trình (*) có:
$
\begin{aligned}
\Delta_{*} &=(S-2)^{2}-4(S-1)(S-2) \\
&=(S-2)(S-2-4 S+4) \\
&=(S-2)(-3 S+2)
\end{aligned}
$
Để tồn tại giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $S$ thì phương trình (*) phải có nghiệm
$
\Leftrightarrow \Delta_{*} \geq 0 \Leftrightarrow(S-2)(-3 S+2) \geq 0
$
Với $S=\dfrac{2}{3}$ ta có:
$
\begin{aligned}
&\dfrac{m^{2}+2 m+2}{m^{2}+m+1}=\dfrac{2}{3} \Leftrightarrow 3 m^{2}+6 m+6=2 m^{2}+2 m+2 \\
&\Leftrightarrow m^{2}+4 m+4=0 \Leftrightarrow(m+2)^{2}=0
\end{aligned}
$
$\Leftrightarrow \quad m+2=0 \quad \Leftrightarrow \quad m=-2$
Với $S=2$ ta có:
$
\begin{aligned}
&\dfrac{m^{2}+2 m+2}{m^{2}+m+1}=2 \\
&\Leftrightarrow m^{2}+2 m+2=2 m^{2}+2 m+2 \Leftrightarrow m^{2}=0 \Leftrightarrow m=0
\end{aligned}
$
Vậy giá trị nhỏ nhất của $S$ là $\dfrac{2}{3}$ khi $m=-2$, giá trị lớn nhất của $S$ là 2 khi $m=0$.