Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 3 (phần tự luận 7 điểm) SVIP
Bài 1. (2,5 điểm) Cho biểu thức $A=\dfrac{x+15}{{{x}^{2}}-9}+\dfrac{2}{x+3}$ với $x\ne \pm 3$.
a) Rút gọn biểu thức $A$.
b) Tìm $x$ để $A$ có giá trị bằng $\dfrac{-1}{2}$.
c) Tìm số tự nhiên $x$ để $A$ nhận giá trị nguyên.
Hướng dẫn giải:
a) Với $x\ne \pm 3$ ta có:
$A=\dfrac{x+15}{{{x}^{2}}-9}+\dfrac{2}{x+3}=\dfrac{x+15}{\left( x+3 \right)\left( x-3 \right)}+\dfrac{2}{x+3}$
$=\dfrac{x+15+2\left( x-3 \right)}{\left( x+3 \right)\left( x-3 \right)}$
$=\dfrac{x+15+2x-6}{\left( x+3 \right)\left( x-3 \right)}$
$=\dfrac{3x+9}{\left( x+3 \right)\left( x-3 \right)}$
$=\dfrac{3\left( x+3 \right)}{\left( x+3 \right)\left( x-3 \right)}=\dfrac{3}{x-3}$
Vậy với $x\ne \pm 3$ thì $A=\dfrac{3}{x-3}.$
b) Với $x\ne \pm 3$, để $A=\dfrac{-1}{2}$ thì $\dfrac{3}{x-3}=\dfrac{-1}{2}$
Suy ra $-x+3=6$
Do đó $x=-3$ (không thỏa mãn)
Vậy không có giá trị nào của $x$ để $A=\dfrac{-1}{2}.$
c) Với $x\ne \pm 3$, để $A$ nguyên thì $\dfrac{3}{x-3}\in \mathbb{Z}$, tức $x-3\in$ Ư$(3)$
Mà Ư$\left( 3 \right)=\left\{ \pm 1;\pm 3 \right\}$, ta có bảng sau:
| $x-3$ | $-3$ | $-1$ | $1$ | $3$ |
| $x$ | $0$ | $2$ | $4$ | $6$ |
Các giá trị $x$ tìm được ở trên đều thỏa mãn điều kiện $x\ne \pm 3$ và $x$ là số tự nhiên.
Vậy $x\in \left\{ 0;2;4;6 \right\}$.
Bài 2. (1 điểm) Phân tích các đa thức sau thành nhân tử:
a) $10{{x}^{2}}\left( 2x-y \right)+6xy\left( y-2x \right);$
b) ${{x}^{2}}-2x+1-{{y}^{2}}$.
Hướng dẫn giải:
a) $10{{x}^{2}}\left( 2x-y \right)+6xy\left( y-2x \right)$
$=10{{x}^{2}}\left( 2x-y \right)-6xy\left( 2x-y \right)$
$=\left( 2x-y \right)\left( 10{{x}^{2}}-6xy \right)$
$=2x\left( 2x-y \right)\left( 5x-3y \right)$.
b) ${{x}^{2}}-2x+1-{{y}^{2}}$
$=\left( {{x}^{2}}-2x+1 \right)-{{y}^{2}}$
$={{\left( x-1 \right)}^{2}}-{{y}^{2}}$
$=\left( x-1-y \right)\left( x-1+y \right).$
Bài 3. (1,5 điểm)
a) Cho tứ giác $ABCD$, biết rằng $\dfrac{\widehat{A\,\,}}{1}=\dfrac{\widehat{B\,}}{2}=\dfrac{\widehat{C\,}}{3}=\dfrac{\widehat{D\,}}{4}.$ Tính $\widehat{B\,}.$
b) Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết $1$ inch $\approx 2,54$ cm điện thoại có chiều rộng là $7$ cm; chiều dài là $15,5$ cm. Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch? (Làm tròn kết quả đến hàng đơn vị)
Hướng dẫn giải:
a) Xét tứ giác $ABCD$ có $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^\circ$
Áp dụng tính chất dãy tỉ số bằng nhau $\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\dfrac{360^\circ }{10}=36^\circ$.
Vậy $\widehat{B}=36^\circ.2=72^\circ .$
b) Áp dụng định lí Pythagore vào tam giác $ABC$ vuông tại $A$ ta có: $B C^{2}=A C^{2}+A B^{2}$
Suy ra $BC=\sqrt{A{{C}^{2}}+A{{B}^{2}}}=\sqrt{{{\left( 15,5 \right)}^{2}}+{{7}^{2}}}\approx 17$ (cm).
Vì $1$ inch $\approx 2,54$ cm nên chiếc điện thoại theo hình vẽ có: $\dfrac{17}{2,54} \approx 7$ inch.
Bài 4. (1 điểm) Cho hình chóp tứ giác đều $S.MNPQ$ như hình vẽ có chiều cao $15$ cm và thể tích là $1$ $280$ cm$^3$.
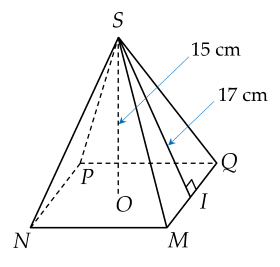
Tính độ dài cạnh đáy của hình chóp.
Hướng dẫn giải:
Diện tích cạnh đáy của hình chóp là:
$S=\dfrac{3V}{h}=\dfrac{3.1280}{15}=256$ (cm$^{2}$)
Độ dài cạnh đáy của hình chóp là:
$S={{a}^{2}}$ nên $a=\sqrt{256}=16$ (cm)
Vậy độ dài cạnh đáy của hình chóp là $16$ cm.
Bài 5. (1 điểm) Một siêu thị niêm yết giá một số loại hoa quả như sau:
| Loại hoa quả | Vải  |
Cam |
Nho |
| Giá mỗi ki-lô-gam (đơn vị: đồng) | $45$ $000$ | $62$ $000$ | $85$ $000$ |
Bác Đô đi siêu thị và mua $x$ kg vải, $y$ kg cam và $z$ kg nho.
a) Viết đa thức $T$ biểu diễn tổng số tiền (đơn vị đồng) bác Đô phải trả.
b) Tính giá trị của đa thức $T$ tại $x=1,5$; $y=3$ và $z=2$.
Hướng dẫn giải:
a) Giá tiền của $x$ kg vải, $y$ kg cam và $z$ kg nho lần lượt là: $45x$; $62y$ và $85z$ (nghìn đồng).
Tổng số tiền bác Đô phải trả là
$T = (45x + 62y + 85z).1 \, 000$ (đồng).
b) Thay $x=1,5$; $y=3$ và $z=2$ vào $(45x + 62y + 85z).1 \, 000$ ta được
$T = (45.1,5 + 62.3 + 85.2).1 \, 000 = 423 \, 500$ (đồng).
