Đề số 3 (Phần tự luận 7 điểm) SVIP

Hướng dẫn giải:

a) $\left( 4{{x}^{4}}-8{{x}^{2}}{{y}^{2}}+12{{x}^{5}}y \right) \, : \, \left( -4{{x}^{2}} \right)$

$=4{{x}^{4}} \, : \, \left( -4{{x}^{2}} \right)-8{{x}^{2}}{{y}^{2}} \, : \, \left( -4{{x}^{2}} \right)+12{{x}^{5}}y \, : \, \left( -4{{x}^{2}} \right)$

$=-{{x}^{2}}+2{{y}^{2}}-3{{x}^{3}}y.$​

b) ${{x}^{2}}\left( x-{{y}^{2}} \right)-xy\left( 1-xy \right)-{{x}^{3}}$

$={{x}^{3}}-{{x}^{2}}{{y}^{2}}-xy+{{x}^{2}}{{y}^{2}}-{{x}^{3}}$

$=-xy.$

Hướng dẫn giải:

a) Đơn thức $A=-13,5xyz$ có hệ số là $-13,5$; phần biến là $xyz$ và bậc bằng $3$. 

b) Nhóm các đơn thức đồng dạng: 

+) ${4}{{{x}}^{{3}}}{{{y}}^{{2}}}$; ${9}{{{x}}^{{3}}}{{{y}}^{{2}}}$

+) $-{0,5}{{{x}}^{{2}}}{{{y}}^{3}}$; $\dfrac{{3}}{{4}}{{{x}}^{{2}}}{{{y}}^{{3}}}$

Hướng dẫn giải:

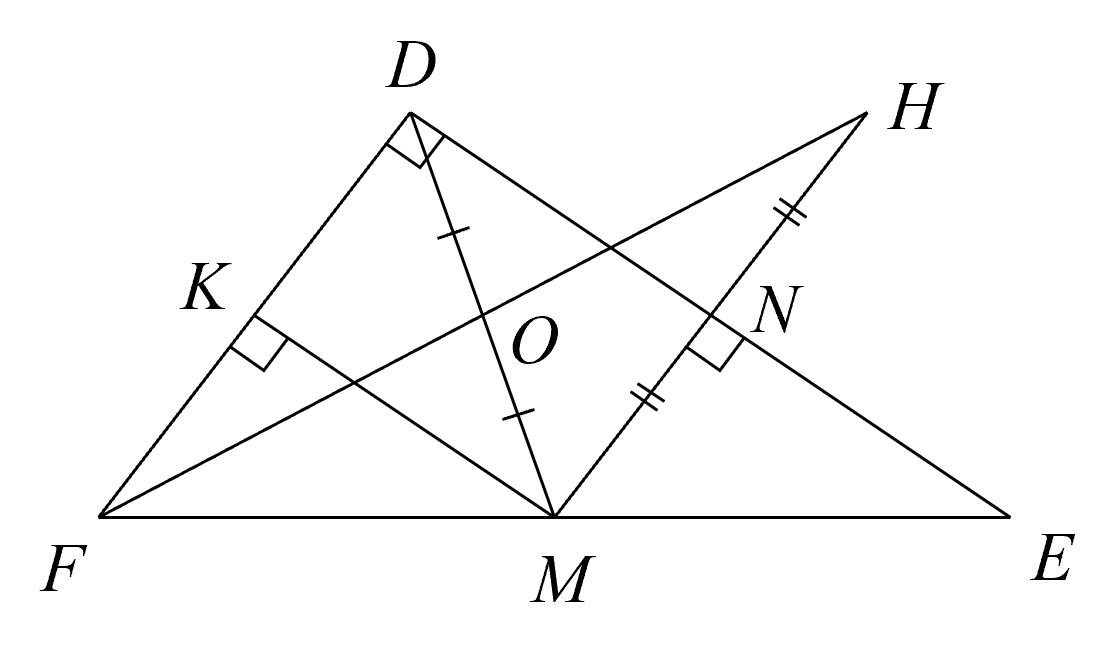
a) Tứ giác $DKMN$ có $\widehat{D\,}=\widehat{K\,}=\widehat{N\,}={{90}^{\circ}}$ nên là hình chữ nhật.

b) Vì $DKMN$ là hình chữ nhật nên $DF$ // $MH$.

Xét $\Delta KFM$ và $\Delta NME$ có:

     $\widehat{K\,}=\widehat{N\,}={{90}^{\circ}}$

     $FM=ME$ (giả thiết)

     $\widehat{KMF}=\widehat{E}$ (đồng vị)

Suy ra $\Delta KFM=\Delta NME$ (cạnh huyền - góc nhọn)

Suy ra $KF=MN$ (hai cạnh tương ứng) mà $MN=DK$ nên $DF=2DK$ và $MH=2MN$.

Do đó $DF=MH$.

Tứ giác $DFMH$ có $DF$ // $MH$, $DF=MH$ nên là hình bình hành.

Nên hai đường chéo $DM, \, FH$ cắt nhau tại trung điểm $O$ của mỗi đường hay $F,\,\,O,\,\,H$ thẳng hàng.

c) Để hình chữ nhật $DKMN$ là hình vuông thì $DK=DN$ $\left( 1 \right)$

Mà $DK=\dfrac{1}{2}DF$ và $DN=KM=NE$ nên $DN=\dfrac{1}{2}DE$ $\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $DF=DE$ nên $\Delta DFE$ cân tại $D$.

Hướng dẫn giải:

a) $(x + y)^2 = x^2 + 2xy + y^2$;

b) $x^2-25 = (x - 5)(x + 5)$.

Hướng dẫn giải:

a) Thay $x = 40$ và $y = 100$ vào $I$ ta có​ chỉ số nhiệt của thành phố $A$ là:

$I_A = -45 + 2.40 + 10.100 - 0,2.40.100 - 0,007.40^2 - 0,05.100^2 + 0,001.40^2.100 + 0,009.40.100^2 - 0,000002.40^2.100^2$

$= -45 + 80 +1 \, 000 -800-11,2 - 500 + 160 + 3 \, 600 - 32 = 3 \, 451,8$.

b) Thay $x = 50$ và $y = 90$ vào $I$ ta có​ chỉ số nhiệt của thành phố $B$ là:

$I_B = -45 + 2.50 + 10.90 - 0,2.50.90 - 0,007.50^2 - 0,05.90^2 + 0,001.50^2.90 + 0,009.50.90^2 - 0,000002.50^2.90^2$

$= -45 + 100 + 900 - 900 - 17,5 - 405 + 160 + 3 \, 645 - 25,92 = 3 \, 411,58 < I_A$.

Vậy không khí ở thành phố $A$ nóng hơn tại thời điểm đó.