Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

a) Cỡ giày 38;

b) Cỡ giày 36; 40; 42.

Hướng dẫn giải:

a) $5,3.4,7+(-1,7) . 5,3-5,9$

$=5,3.(4,7-1,7)-5,9$

$=5,3.3-5,9$

$=15,9-5,9=10$

b) $\dfrac{2}{3}+\dfrac{-1}{3}+\dfrac{7}{15}$

$=\dfrac{2+(-1)}{3}+\dfrac{7}{15}$

$=\dfrac{5+7}{15}=\dfrac{12}{15}=\dfrac{4}{5}$.

Hướng dẫn giải:

a) Hình vuông với diện tích $10$ cm$^2$ có độ dài cạnh bằng $\sqrt{10}$.

Sử dụng MTCT ta tính được $\sqrt{10}=3,4622...$

Làm tròn kết quả đến cữ số thập phân thứ hai ta được độ dài cạnh hình vuông cần tính là $3,46 $ cm.

b) Uớc lượng số liệu với độ chính xác $500$ nên phải làm tròn số đến hàng nghìn.

Số dân thành phố uớc tính là $7$ $343$ $000$ người.

Hướng dẫn giải:

a) Học sinh vẽ hình đúng, ghi đúng GT - KL.

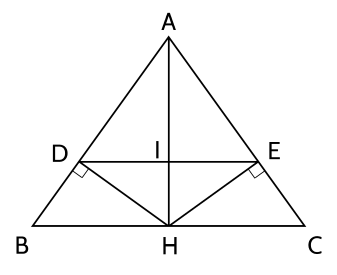
Xét $\Delta ABD$ và $\Delta ACH$ có:

$AH$ là cạnh chung;

$\widehat{BAH} = \widehat{CAH}$ (GT)

$AB = AC$ (GT)

Suy ra $\Delta ABD=\Delta ACH$ (c.g.c).

b) 

Ta có $\Delta ABD=\Delta ACH$ (câu a).

$\Rightarrow \widehat{AHB} = \widehat{AHC}$ (hai góc tương ứng)

Mà $\widehat{AHB} + \widehat{AHC} = 180^{\circ}$ (hai góc kề bù).

Suy ra $\widehat{AHB} = \widehat{AHC} = 90^{\circ}$ hay $AH \perp BC$.

c) Vẽ $HD \perp BC$ với $D\in AB$; $HE \perp AC$ với $E \in AC$.

Xét hai tam giác vuông $\Delta ADH$ và $\Delta AEH$ có:

$AH$ là cạnh chung

$\widehat{BAH} = \widehat{CAH}$ (GT)

Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).

Suy ra $HD = HE$ (hai cạnh tương ứng).

Hướng dẫn giải:

$\dfrac{x+2022}{\sqrt{25}}-\dfrac{x+|-2022|}{3}=\dfrac{x}{2}+1011$

$\dfrac{x+2022}{5}-\dfrac{x+2022}{3}-\dfrac{x+2022}{2}=0$

$\left(\dfrac{1}{5}-\dfrac{1}{3}-\dfrac{1}{2}\right)(x+2022)=0 $

$(x+2022)=0$

$x=-2022$.