Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (7 điểm) SVIP
Câu 13. (0,5 điểm): Tính giá trị $\left(2+\dfrac{1}{3}-0,4\right)-\left(7-\dfrac{3}{5}-\dfrac{4}{3}\right)-\left(\dfrac{1}{5}+\dfrac{5}{3}-4\right)$.
Hướng dẫn giải:
$\left(2+\dfrac{1}{3}-0,4\right)-\left(7-\dfrac{3}{5}-\dfrac{4}{3}\right)-\left(\dfrac{1}{5}+\dfrac{5}{3}-4\right)$
$=(2-7+4-0,4)+\left(\dfrac{3}{5}-\dfrac{1}{5}\right)+\left(\dfrac{1}{3}+\dfrac{4}{3}-\dfrac{5}{3}\right)$
$=(-1-0,4)+\dfrac{2}{5}+0$
$=-1-0,4+0,4=-1$.
Câu 14. (0,5 điểm): Làm tròn số 7 891 233 với độ chính xác $d$ = 5 000.
Hướng dẫn giải:
Cần làm tròn số đến hàng vạn (10 000)
Kết quả làm tròn là số 7 890 000.
Câu 15. (0,5 điểm): Viết giả thiết, kết luận của định lí: "Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau."
Hướng dẫn giải:
Giả thiết: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.
Kết luận: Chúng song song với nhau.
Câu 16. (1,0 điểm): Cho biết công thức tính diện tích hình tròn bán kính ${R}$ là ${S}=\pi {R}^2$. Sử dụng MTCT, hãy tính độ dài bán kính (tính theo đơn vị xen ti mét - với độ chính xác $d=0,05$) của hình tròn có diện tích bằng $100$ cm$^2$.
Hướng dẫn giải:
Thay $S=100$ vào $S=\pi R^2$ ta được $\pi R^2=100$.
Suy ra $R=\sqrt{\dfrac{100}{\pi}}$.
Sử dụng MTCT tính được $R=5,641895835...$
Cần làm tròn đến hàng phần chục để có độ chính xác ${d}=0,05$.
Kết quả là $R \approx 5,6$.
Câu 17. (2,0 điểm): Cho $\Delta A B C$ cân tại $A$, $M$ là trung điểm của cạnh $B C$.
a) (1,0 điểm) Chứng minh $\Delta A M B=\Delta A M C$.
b) (0,5 điểm) Từ $M$ kẻ $M E \perp A B$, $(E \in A B)$, $M F \perp A C$, $(F \in A C)$. Chứng minh $E A=F A$.
c) (1,0 điểm) Chứng minh $E F$ // $B C$.
Hướng dẫn giải:
a) Vẽ đúng hình:

Xét $\Delta A M B$ và $\Delta A M C$ có:
$A B=A C$,
$\widehat{B}=\widehat{C}$ (do giả thiết $\Delta A B C$ cân tại $A)$
$M B=M C$ (do giả thiết $M$ là trung điểm của cạnh $B C$)
Do đó $\Delta A M B=\Delta A M C$ (c.g.c).
b) Do giả thiết $M E \perp A B$, $(E \in A B)$;
$M F \perp A C$, $(F \in A C)$ suy ra $\Delta E M B$ và $\Delta F M C$ là hai tam giác vuông (ở $E$ và $F$).
Mà $M B=M C$, $\widehat{B}=\widehat{C}$ (chứng minh trong a)).
Do đó $\Delta E M B=\Delta F M C$ (cạnh huyền-góc nhọn).
Suy ra $E B=F C$ (cạnh tương ứng).
Mà $A B=A C$ nên $E A=A B-E B=A C-F C=F A$.
c) $\Delta A E F$ cân ở $A$ (do $E A=F A$ theo chứng minh trên) nên $\widehat{A EF}=\left(180^{\circ}-\widehat{A}\right) \, : \, 2$
Tương tự, $\Delta A B C$ cân ở $A$ (giả thiết) nên $\widehat{A B C}=\left(180^{\circ}-\widehat{A}\right) \, : \, 2$
Do đó $\widehat{A E F}=\widehat{A B C}$, suy ra $E F$ // $B C$.
Câu 18. (2,5 điểm): Căn cứ vào biểu đồ dưới đây về tỉ lệ phần trăm loại quả được bán ra trong ngày của một cửa hàng để trả lời các câu hỏi sau:
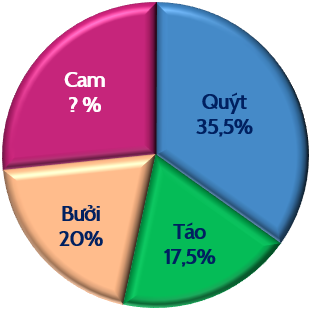
a) (0,5 điểm) Tỉ lệ phần trăm lượng cam tiêu thụ được là bao nhiêu?
b) (0,5 điểm) Hai loại quả có lượng tiêu thụ nhiều nhất là gì?
c) (0,5 điểm) Tổng lượng cam và bưởi tiêu thụ được là bao nhiêu phần trăm?
d) (1,0 điểm) Biết cửa hàng bán được $135$ kg quả các loại trong ngày. Tính số cam cửa hàng bán được trong ngày hôm đó.
Hướng dẫn giải:
a) Tỉ lệ phần trăm lượng cam tiêu thụ được là $100-(20+17,5+35,5)=27 \%$
b) Do $35,5>27>20>17,5$ nên hai loại quả có lượng tiêu thụ nhiều nhất là quýt và cam.
c) Tổng lượng cam và bưởi tiêu thụ được là $27+20=47 \%$.
d) $135$ kg cam bằng $27 \%$ toàn bộ số quả bán được nên $100 \%$ số quả bán được là:
$135 \, : \, 27 \%=500$ kg.
