Đề số 2 (thời gian: 90') SVIP

Hướng dẫn giải:

a) $2 \sqrt{45}+\sqrt{5}-3 \sqrt{80}$
$2 \sqrt{45}+\sqrt{5}-3 \sqrt{80}$
$=2 \sqrt{9.5}+\sqrt{5}-3 \sqrt{16.5}$
$=2 \sqrt{3^2 \cdot 5}+\sqrt{5}-3 \sqrt{4^2 .5}$
$=2.3 \sqrt{5}+\sqrt{5}-3.4 \sqrt{5}$
$=6 \sqrt{5}+\sqrt{5}-12 \sqrt{5}$
$=-5 \sqrt{5}$.
b) $\sqrt{(2-\sqrt{3})^2}+\dfrac{2}{\sqrt{3}+1}-6 \sqrt{\dfrac{16}{3}}$
$=|2-\sqrt{3}|+\dfrac{2(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}-6 \sqrt{\dfrac{4^2}{3}}$
$=2-\sqrt{3}+\dfrac{2(\sqrt{3}-1)}{(\sqrt{3})^2-1^2}-6 \dfrac{4}{\sqrt{3}}($ do $2>\sqrt{3}$ nên $|2-\sqrt{3}|=2-\sqrt{3})$
$=2-\sqrt{3}+\dfrac{2(\sqrt{3}-1)}{2}-8 \sqrt{3}$
$=2-\sqrt{3}+\sqrt{3}-1-8 \sqrt{3}$
$=1-8 \sqrt{3}$.

c) $\tan ^2 40^{\circ} \cdot \sin ^2 50^{\circ}-3+\left(1-\sin 40^{\circ}\right)\left(1+\sin 40^{\circ}\right)$
$\begin{aligned} &=\tan ^2 40^{\circ} \cdot \sin ^2 50^{\circ}-3+\left(1-\sin ^2 40^{\circ}\right) \\ &=\frac{\sin ^2 40^{\circ}}{\cos ^2 40^{\circ}} \cdot \cos ^2 40^{\circ}-3+1-\sin ^2 40^{\circ} \\ &=\sin ^2 40^{\circ}-3+1-\sin ^2 40^{\circ} \\ &=-2 \end{aligned}$.

Hướng dẫn giải:

a) ĐKXĐ: $x\leq \dfrac{4}{3}$
$\begin{aligned} & \sqrt{4-3 x}=8  \\ &\Leftrightarrow(\sqrt{4-3 x})^2=8^2 \\ &\Leftrightarrow 4-3 x=64 \\ &\Leftrightarrow x=-20 (\text{thoả mãn}) \end{aligned}$
Vậy phương trình có nghiệm $x=-20$.

b) $\sqrt{4 x-8}-12 \sqrt{\dfrac{x-2}{9}}=-1$
Điều kiện xác định: $x-2 \geq 0 \Leftrightarrow x \geq 2$
$$ \begin{aligned} &\sqrt{4 x-8}-12 \sqrt{\dfrac{x-2}{9}}=-1 \\ &\Leftrightarrow \sqrt{4(x-2)}-12 \sqrt{\dfrac{1}{9}(x-2)}=-1 \\ &\Leftrightarrow 2 \sqrt{x-2}-12 \cdot \dfrac{1}{3} \sqrt{x-2}=-1 \\ &\Leftrightarrow 2 \sqrt{x-2}-4 \sqrt{x-2}=-1 \\ &\Leftrightarrow 2 \sqrt{x-2}=1 \\ &\Leftrightarrow \sqrt{x-2}=\dfrac{1}{2} \\ &\Leftrightarrow x-2=\dfrac{1}{4} \\ &\Leftrightarrow x=\dfrac{9}{4} \text { (thỏa mãn) } \end{aligned}$$
Vậy phương trình có nghiệm $x=\dfrac{9}{4}$.

Hướng dẫn giải:

a)Tính giá trị biểu thức $\mathrm{B}$ khi $x=36$.
Khi $x=36$ (thỏa mãn điều kiên xác định $x>0, x \neq 1, x \neq 9$ ), ta có:
$B=\dfrac{\sqrt{36}}{\sqrt{36}-3}=\dfrac{6}{6-3}=2$
Vậy $B=2$.
b) Tìm $x$ để $B<\dfrac{1}{2}$
Ta có:

$$\begin{aligned}&B<\dfrac{1}{2} \\ &\Leftrightarrow \dfrac{\sqrt{x}}{\sqrt{x}-3}<\dfrac{1}{2} \\ &\Leftrightarrow \dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{1}{2}<0 \\ &\Leftrightarrow \dfrac{2 \sqrt{x}-\sqrt{x}+3}{2(\sqrt{x}-3)}<0 \\ &\Leftrightarrow \dfrac{\sqrt{x}+3}{2(\sqrt{x}-3)}<0 \\ &\Leftrightarrow 2(\sqrt{x}-3)<0 \text { (do } \sqrt{x}+3>0 \quad \forall x>0, x \neq 1, x \neq 9) \\ &\Leftrightarrow \sqrt{x}-3<0 \\ &\Leftrightarrow \sqrt{x}<3 \\ &\Leftrightarrow x<9 \end{aligned}$$
Kết hợp với điều kiện xác định, ta có $\left\{\begin{array}{l}0<x<9 \\ x \neq 1\end{array}\right.$ là giá trị cần tìm.
c) Rút gọn biểu thức $\mathrm{A}$.
$A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right): \dfrac{\sqrt{x}+1}{\sqrt{x}+2}$ 
$=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}(\sqrt{x}-1)}\right)$ $\cdot \dfrac{\sqrt{x}+2}{\sqrt{x}+1}$
$=\left(\dfrac{x}{\sqrt{x}(\sqrt{x}-1)}-\dfrac{1}{\sqrt{x}(\sqrt{x}-1)}\right) \cdot \dfrac{\sqrt{x}+2}{\sqrt{x}+1}$
$=\dfrac{x-1}{\sqrt{x}(\sqrt{x}-1)} \cdot \dfrac{\sqrt{x}+2}{\sqrt{x}+1}$
$=\dfrac{(\sqrt{x}+1)(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-1)} \cdot \dfrac{\sqrt{x}+2}{\sqrt{x}+1}$
$=\dfrac{\sqrt{x}+2}{\sqrt{x}}$
d)Tìm giá trị $x$ nguyên nhỏ nhất để biểu thức $P=A \cdot B$ nguyên.
$$ P=A \cdot B=\dfrac{\sqrt{x}+2}{\sqrt{x}} \cdot \dfrac{\sqrt{x}}{\sqrt{x}-3} $$
$$ \begin{aligned} &=\dfrac{\sqrt{x}+2}{\sqrt{x}-3} \\ &=\dfrac{\sqrt{x}-3+5}{\sqrt{x}-3} \\ &=1+\dfrac{5}{\sqrt{x}-3} \end{aligned} $$

Ta có: $P=A . B$ nguyên $\Leftrightarrow 1+\dfrac{5}{\sqrt{x}-3}$ nguyên $\Leftrightarrow \dfrac{5}{\sqrt{x}-3}$ nguyên $\Leftrightarrow 5:(\sqrt{x}-3)$
$$\begin{aligned} &\Leftrightarrow \sqrt{x}-3 \in\{-5 ;-1 ; 1 ; 5\} \\ &\Leftrightarrow \sqrt{x} \in\{-2 ; 2 ; 4 ; 8\} \\ &\Leftrightarrow \sqrt{x} \in\{2 ; 4 ; 8\}(\text { do } \sqrt{x} \geq 0 \forall x \geq 0) \\ &\Leftrightarrow x \in\{4 ; 16 ; 64\} \end{aligned}$$
Vậy $x=4$ là giá trị nguyên nhỏ nhất để biểu thức $P=A \cdot B$ nguyên.

Hướng dẫn giải:

a) 

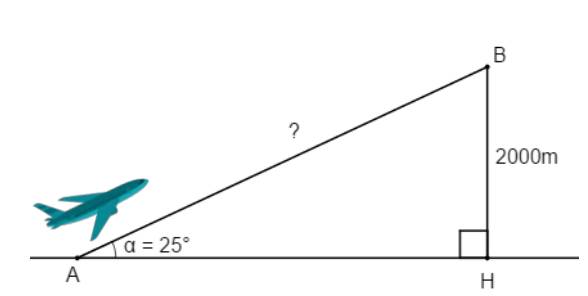
Xét $\triangle A B C$ vuông tại $H$ có:
$$\dfrac{B H}{A B}=\sin \widehat{B A H} \Leftrightarrow \dfrac{2000}{A B}=\sin 25^{\circ} \Leftrightarrow A B=\dfrac{2000}{\sin 25^{\circ}} \approx 4732,4(\mathrm{~m})$$
Vậy muốn đạt độ cao $2000 \mathrm{~m}$ thì máy bay phải bay một đoạn đường $4732,4 \mathrm{~m}$.

b) Kẻ $H D, H E$ lần lượt vuông góc với $A B, A C$ ( $D$ thuộc $A B, E$ thuộc $A C$ ). Chứng minh $B D \cdot D A+C E \cdot E A=A H^2$.
Xét $\triangle A B H$ vuông tại $H, D H$ là đường cao.

Ta có $H D^2=B D \cdot D A$
Xét $\triangle A H C$ vuông tại $H$, đường cao $H E$ có:
$H E^2=A E \cdot E C$
Vì $\widehat{D A E}=\widehat{A E H}=\widehat{E H D}=\widehat{H D A}=90^{\circ}$ nên tứ giác $D A E H$ là hình chữ nhật.
$$\Rightarrow H E=D A$$
Xét $\triangle A D H$ vuông tại $D$ có:
$D A^2+D H^2=A H^2$
$\Rightarrow H E^2+D H^2=A H^2(d o H E=D A)$ $\Rightarrow B D \cdot D A+C E \cdot E A=A H^2$
c)Lấy điểm $M$ nằm giữa $E$ và $C$, kẻ $A I$ vuông góc với $M B$ tại $I$. Chứng minh $\sin \widehat{A M B} \cdot \sin \widehat{A C B}=\dfrac{H I}{C M}$

- Xét $\triangle A B M$ vuông tại $A$ có đường cao $A I$
Áp dụng hệ thức lượng trong tam giác vuông ta có : $B I . B M=A B^2$ Xét $\triangle A B C$ vuông tại $A$ có đường cao $A H$
Áp dụng hệ thức lượng trong tam giác vuông ta có : $B H . B C=A B^2$
$\Rightarrow B I . B M=B H \cdot B C\left(=A B^2\right)$
$\Rightarrow \dfrac{B H}{B M}=\dfrac{B C}{B I}$
- Xét $\triangle A H I$ và $\triangle B M C$ có
$\dfrac{B H}{B M}=\dfrac{B C}{B I}$
$\widehat{I B C}$ chung
$\Rightarrow \triangle A H I = \triangle B M C$ (c-g-c)
Suy ra: $\dfrac{H I}{M C}=\dfrac{B I}{B C}$.
- Xét $\triangle A B M$ vuông tại $A$ ta có: $\sin \widehat{A M B}=\dfrac{A B}{B M}$
- Xét $\triangle A B C$ vuông tại $A$ ta có: $\sin \widehat{A C B}=\dfrac{A B}{B C}$
$\Rightarrow \sin \widehat{A B M} \cdot \sin \widehat{A C B}=\dfrac{A B}{B M} \cdot \dfrac{A B}{B C}=\dfrac{A B^2}{B M \cdot B C}$ mà $B I \cdot B M=A B^2$
$\Rightarrow \sin \widehat{A B M} \cdot \sin \widehat{A C B}=\dfrac{A B^2}{B M \cdot B C}=\dfrac{B I \cdot B M}{B M \cdot B C}=\dfrac{B I}{B C}$ mà $\dfrac{H I}{M C}=\dfrac{B I}{B C}$
$\Rightarrow  \sin \widehat{A B M} \cdot \sin \widehat{A C B}=\dfrac{H I}{M C}(\text{dpcm})$.

Hướng dẫn giải:

ĐKХĐ: $x \geq \frac{1}{2}$
Với $x \geq \frac{1}{2}$ ta có:
$ \begin{aligned} &2\left(x-\sqrt{2 x^2+5 x 3}\right)=1+x(\sqrt{2 x-1}-2 \sqrt{x+3}) \\ &\Leftrightarrow 2 x-1-2 \sqrt{2 x^2+5 x-3}-x(\sqrt{2 x-1}-2 \sqrt{x+3})=0(1) \\ &\text { Đặt }\left\{\begin{array}{l} \sqrt{2 x-1}=a \\ \sqrt{x+3}=b \end{array}(a \geq 0, b>0)\right. \\ &\Rightarrow\left\{\begin{array}{l} 2 x-1=a^2 \\ x=b^2-3 \\ \sqrt{2 x^2+5 x-3}=a b \end{array}\right. \end{aligned} $

Phương trình $(1)$ trở thành: 
$ \begin{aligned} &a^2-2 a b-\left(b^2-3\right)(a-2 b)=0 \\ &\Leftrightarrow a^2-2 a b-a b^2+2 b^3+3 a-6 b=0 \\ &\Leftrightarrow a(a-2 b)-b^2(a-2 b)+3(a-2 b)=0 \\ &\Leftrightarrow(a-2 b)\left(a-b^2+3\right)=0 \\ &\Leftrightarrow\left[\begin{array}{l} a=2 b \\ b^2=a+3 \end{array}\right. \\ &+) \text { Nếu } a=2 b \text { ta có: } \\ &\sqrt{2 x-1}=2 \sqrt{x+3} \\ &\Leftrightarrow 2 x-1=4 x+12 \\ &\Leftrightarrow 2 x=-13 \\ &\Leftrightarrow x=\dfrac{-13}{2} \text { (không thỏa mãn điều kiện) }\end{aligned} $.

+) Nếu $b^2=a+3$ ta có:
$x+3=\sqrt{2 x-1}+3$
$\Leftrightarrow \sqrt{2 x-1}=x$
$\Leftrightarrow 2 x-1=x^2$
$\Leftrightarrow x^2-2 x+1=0$
$\Leftrightarrow(x-1)^2=0$
$\Leftrightarrow x-1=0$ $\Leftrightarrow x=1$ (thỏa mãn điều kiện)
Vậy phương trình có tập nghiệm $S=\{1\}$.