Đề số 2 - bộ Kết nối tri thức với cuộc sống

Câu 1 (1đ):

Cho parabol $\left(P \right)$ có phương trình $y=3x^2+2x+1$ . Trục đối xứng của parabol là đường thẳng

x=-\dfrac{2}{3}

.

x=-\dfrac{1}{3}

.

x=\dfrac{2}{3}

.

x=\dfrac{1}{3}

.

Câu 2 (1đ):

Cho tam thức bậc hai $f(x)=2x^2+bx+c$ có $\Delta<0$ với $b, \, c$ là các số thực. Phát biểu nào sau đây đúng?

f\left(x \right)<0, \, \forall x\in \mathbb{R}

.

Phương trình

f\left(x \right)=0

có nghiệm.

f\left(x \right)<0, \, \forall x\in \left(0;+\infty \right)

.

f\left(x \right)>0 ,\, \forall x\in \mathbb{R}

.

Câu 3 (1đ):

Biểu thức nào sau đây là tam thức bậc hai (đối với $x$ )?

f\left(x \right)=-\dfrac{5}{3}x^2+\dfrac{7}{2}x-6

.

f\left(x \right)=-5x^4+3x^2+4

.

f\left(x \right)=\left(\dfrac{1}{x} \right)^2+4\dfrac{1}{x}-5

.

f\left(x \right)=2x-3\sqrt{x}+5

.

Câu 4 (1đ):

Điểm nào sau đây thuộc đồ thị hàm số $y=x^2-2x+4$ ?

\left(0;4 \right)

.

\left(0;-4 \right)

.

\left(4;0 \right)

.

\left(4;4 \right)

.

Câu 5 (1đ):

Hàm số $y=x^2-4x+3$ đồng biến trên khoảng nào trong các khoảng dưới đây?

\left(-\infty ;2 \right)

.

\left( 2;+\infty \right)

.

\left( -\infty ;+\infty \right)

.

\left( -2;+\infty \right)

.

Câu 6 (1đ):

Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng $\Delta:\left\{ \begin{aligned} & x=5-\dfrac{1}{2}t \\ & y=-3+3t \\ \end{aligned} \right.$ ?

\overrightarrow{u}=\left(-1;6 \right).

\overrightarrow{u}=\left(-5;3 \right)

.

\overrightarrow{u}=\left(\dfrac{1}{2};3 \right)

.

\overrightarrow{u}=\left(5;-3 \right)

.

Câu 7 (1đ):

Cho parabol $\left(P \right): \, y=ax^2+bx+c$ có đồ thị như hình vẽ bên dưới:

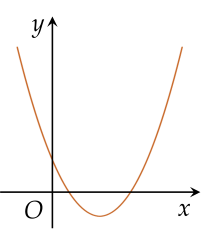
olm đề thi giữa kì 2 toán 10 mới

Chọn đáp án đúng.

a<0, \, b>0, \, c<0

.

a>0, \, b>0, \, c<0

.

a>0, \, b<0, \, c>0

.

a>0, \, b>0, \, c>0

.

Câu 8 (1đ):

Tam thức nào sau đây luôn dương với mọi $x \in \mathbb{R}$ ?

f\left(x \right)=x^2-6x+9

.

f\left(x \right)=-2x^2-1

.

f\left(x \right)=x^2-2x-3

.

f\left(x \right)=2x^2+x+1

.

Câu 9 (1đ):

Tập nghiệm của bất phương trình $4x^2+9x+2>0$ là

\left( -\infty ;\dfrac{1}{4} \right)\cup \left( 2;+\infty \right)

.

\left( -\infty ;-2 \right) \cup \left(-\dfrac{1}{4};+\infty \right)

.

\left( \dfrac{1}{4};2 \right)

.

\left( -2;-\dfrac{1}{4} \right)

.

Câu 10 (1đ):

Tập xác định của hàm số $y=\dfrac{3x+4}{\left(x-2 \right)\sqrt{x+4}}$ là

\left(-4;+\infty \right)

.

\left(-4;+\infty \right)\backslash \left\{ 2 \right\}

.

\left[ -4;+\infty \right]\backslash \left\{ 2 \right\}

.

\mathbb{R}\backslash \left\{ 2 \right\}

.

Câu 11 (1đ):

Tập nghiệm của phương trình $\sqrt{2x^2-5x+3}=\sqrt{x^2-2x+1}$ là

S=\left\{ 1 \right\}

.

S=\varnothing

.

S=\left\{ 2 \right\}

.

S=\left\{ 1;2 \right\}

.

Câu 12 (1đ):

Trong mặt phẳng $Oxy$ , cho đường thẳng $\Delta$ có phương trình tham số $\left\{ \begin{aligned}& x=2+t \\ & y=-1+3t \\ \end{aligned} \right.$ , với $t$ là tham số. Khi đó, phương trình tổng quát của $\Delta$ là

3x-y+7=0

.

x-3y+5=0

.

x-3y-5=0

.

3x-y-7=0

.

Câu 13 (1đ):

Cho biểu thức $f\left(x \right)=-x^2+5x-6$ .

(Nhấp vào dòng để chọn đúng / sai)

$f\left(x \right)>0\Leftrightarrow x\in \left(2;3 \right).$
$f\left(x \right)<0\Leftrightarrow x\in \left(-\infty ;-3 \right)\cup (-2;+\infty).$
$f\left(x \right)\ge 0\Leftrightarrow x\in \left(2;3 \right).$
$f\left(x \right)\le 0\Leftrightarrow x\in \left(-\infty ;2 \right]\cup \left[ 3;+\infty \right).$

Câu 14 (1đ):

Cho hàm số $y=f\left(x \right)$ có đồ thị dạng parabol như hình bên dưới.

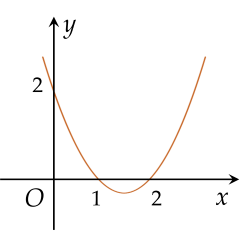
olm đề thi giữa kì 2 toán 10 mới

(Nhấp vào dòng để chọn đúng / sai)

Parabol trên là đồ thị của hàm số $f\left(x \right)=x^2-3x+2$ .
Khoảng nghịch biến của hàm số $f(x)$ là $\left(-\infty \,;\,1 \right)$ và $\left(2\,;\,+\infty \right)$ .
$f\left(x \right)>0\,,\,\forall x\in \left(-\infty \,;\,1 \right)\cup \left(2\,;\,+\infty \right)$ .
Tập nghiệm của bất phương trình $f\left(x \right)\le 0$ là $S=\left(1;2 \right)$ .

Câu 15 (1đ):

Trong mặt phẳng toạ độ $Oxy$ , cho hai điểm $A\left(2;-1 \right)$ và $B\left(0;3 \right)$ .

(Nhấp vào dòng để chọn đúng / sai)

Phương trình của đường thẳng $AB$ là $2x+y-3=0$ .
Đường thẳng $AB$ có một vectơ pháp tuyến là $\overrightarrow{n}=\left(-2; 4 \right)$ .
Đường thẳng $AB$ vuông góc với đường thẳng $2x+y+4=0$ .
Đường thẳng $AB$ đi qua điểm $M\left(1;1 \right)$ .

Câu 16 (1đ):

Trong mặt phẳng toạ độ $Oxy$ , cho hai điểm $A\left(1;1 \right)$ và $B\left(7;5 \right)$ .

(Nhấp vào dòng để chọn đúng / sai)

Phương trình của đường tròn đường kính $AB$ là ${{\left(x-4 \right)}^{2}}+{{\left(y-3 \right)}^{2}}=13$ .
Đường tròn tâm $A\left(1;\,1 \right)$ và tiếp xúc với đường thẳng $\Delta:5x+12y+9=0$ có bán kính là $2$ .
Phương trình của đường tròn tâm $I\left(2;\,-3 \right)$ và đi qua $A\left(1;1 \right)$ là ${{\left(x-1 \right)}^{2}}+{{\left(y-1 \right)}^2}=17$ .
Điểm $M\left(5;\,3 \right)$ thuộc đường tròn tâm $B\left(7;5 \right)$ bán kính $3$ .

Câu 17 (1đ):

Có bao nhiêu số nguyên $m \in \left[ -2\,024;\,2\,024 \right]$ để hàm số $y=\sqrt{m-2x}$ xác định trên khoảng $\left(-3;-1 \right)$ ?

Đáp án:

Câu 18 (1đ):

Hai hòn đảo $A$ và $B$ cách nhau $20$ km. Từ một vị trí $S$ trên đất liền, một con tàu đi thẳng đến hòn đảo $A$ . Tuy nhiên khi đi đến vị trí $M$ cách $S$ một khoảng $30$ km thì con tàu bị chết máy. Khi đó con tàu cách hòn đảo $A$ bao nhiêu km? Biết rằng $AB$ tạo với phương mà con tàu di chuyển một góc $120^\circ$ và quãng đường từ hòn đảo $B$ đến $M$ bằng một nửa quãng đường từ hòn đảo $B$ đến $S$ .

olm đề thi giữa kì 2 toán 10 mới

Đáp án: km.

Câu 19 (1đ):

Trong mặt phẳng tọa độ $Oxy$ , cho đường thẳng $\Delta: \, ax+by+c=0$ với $a, \, b>0$ đi qua giao điểm của hai đường thẳng $d_1: \, 2x+y-3=0$ và $d_2: \, x-2y+1=0$ đồng thời tạo với đường thẳng $d_3: \, y-1=0$ một góc $45^\circ$ . Tính $2\,024.\dfrac{a}{b}$ .

Đáp án:

Câu 20 (1đ):

Trong mặt phẳng tọa độ $Oxy$ , cho biết điểm $M\left(a;b \right)\,$ $\left(a>0 \right)$ thuộc đường thẳng $d: \, \left\{ \begin{aligned}& x=3+t \\ & y=2+t \\ \end{aligned} \right.$ và cách đường thẳng $\Delta: \, 2x-y-3=0$ một khoảng $2\sqrt{5}$ . Tính $a+b$ .

Đáp án:

Câu 21 (1đ):

Có hai con tàu $A$ và $B$ cùng xuất phát từ hai bến, chuyển động đều theo đường thẳng ngoài biển. Trên màn hình radar của trạm điều khiển (được coi như mặt phẳng tọa độ $Oxy$ với đơn vị trên các trục tính theo ki - lô - mét), sau khi xuất phát $t$ (giờ), $\left(t \ge 0 \right)$ , vị trí của tàu $A$ có tọa độ được xác định bởi công thức $\left\{ \begin{aligned}& x=3-35t \\ & y=-4+25t \\ \end{aligned} \right.$ , vị trí của tàu $B$ có tọa độ là $N(4-30t; 3-40t)$ . Hỏi khi hai tàu gần nhau nhất thì cách nhau bao nhiêu ki - lô - mét? (làm tròn kết quả đến hàng phần trăm).

Đáp án:

Câu 22 (1đ):

Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe honda Future Fi với chi phí mua vào một chiếc là $27$ (triệu đồng) và bán ra với giá là $31$ triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là $600$ chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm $1$ triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm $200$ chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất?

Đáp án: triệu đồng. (ghi kết quả dưới dạng số thập phân)

Bài học cùng chủ đề

Đề số 2 - bộ Kết nối tri thức với cuộc sống SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề số 2 - bộ Kết nối tri thức với cuộc sống SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP