Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 3) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=2x−43x−1. Khẳng định nào sau đây đúng?
Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu của f′(x) như sau:
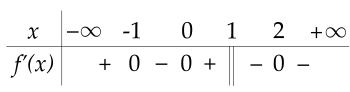
Số điểm cực đại của hàm số đã cho là
Cho hàm số y=f(x) có bảng biến thiên sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y=x4−2x2+3 lần lượt là
Cho đồ thị hàm số y=f(x) có đồ thị như hình vẽ:
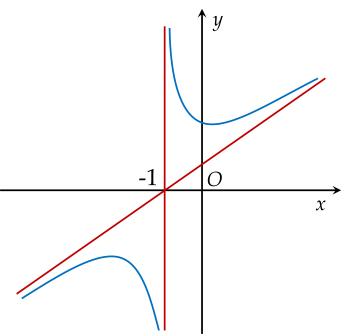
Tiệm cận đứng của đồ thị hàm số là đường thẳng
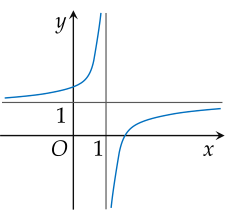
Đồ thị của hàm số nào dưới đây có hình dạng như hình vẽ?
Biết đường thẳng y=x−2 cắt đồ thị hàm số y=x−12x+1 tại hai điểm phân biệt A và B có hoành độ xA,xB. Giá trị của biểu thức xA+xB bằng
Điểm nào sau đây thuộc đồ thị của hàm số y=x4−3x2−5?
Số lượng sản phẩm của công ty bán được trong x (tháng) được tính bởi công thức S(x)=300(2+x+24) với x≥1. Xem y=S(x) là một hàm số xác định trên [1;+∞), khi đó tiệm cận ngang của đồ thị hàm số đó là
Với giá trị nào dưới đây của m thì hàm số y=cos2x+mx đồng biến trên R?
Số giá trị nguyên dương của tham số m để đồ thị hàm số y=x2−8x+mx−1 có 3 đường tiệm cận là
Cho hàm số y=f(x) liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ.
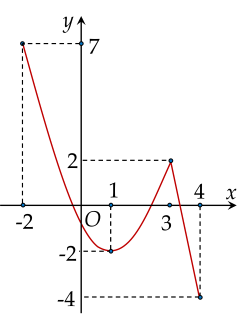
| a) Trên đoạn [−2;4], đồ thị hàm số y=f(x) có 2 điểm cực trị. |
|
| b) Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;2] là −2. |
|
| c) Giá trị lớn nhất của hàm số y=f(x) trên đoạn [1;4] là −4. |
|
| d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;4] là 11. |
|
Cho hàm số y=f(x), có đồ thị như hình vẽ:
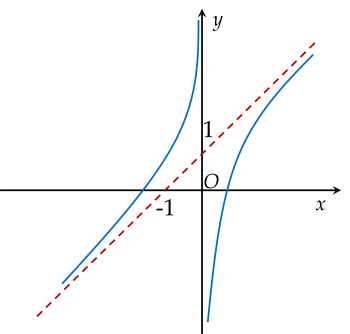
| a) Tiệm cận xiên của đồ thị hàm số y=f(x) là đường thẳng y=x+1. |
|
| b) Tiệm cận đứng của đồ thị hàm số là x=0. |
|
| c) x→+∞limxf(x)=2. |
|
| d) x→+∞lim[f(x)−x]=3. |
|
Một khúc gỗ có dạng hình khối nón có bán kính đáy r=2 m, chiều cao l=6 m. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ.
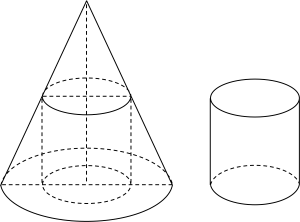
| a) Đặt x là bán kính đáy hình trụ, h là chiều cao của hình trụ. Khi đó chiều cao của khối trụ tính theo bán kính đáy hình trụ là h=−3x+6 (m) với 0<x<2. |
|
| b) Hàm số xác định thể tích của khối trụ trên là V=6x2−3x3 (m3), ∀x∈(0;2). |
|
| c) Giả sử bác thợ mộc chế tác khúc gỗ đó thành hình trụ có bán kính đáy bằng chiều cao, khi đó thể tích của khối trụ là V=827π (m3). |
|
| d) Thể tích lớn nhất của khối gỗ mà bác thợ mộc chế tác là Vmax=932π (m3). |
|
Cho hàm số y=f(x) có bảng biến thiên như sau:
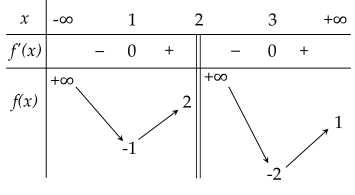
| a) Giá trị nhỏ nhất của hàm số trên [−2,5;1,5] là −2. |
|
| b) Hàm số xác định và liên tục trên R. |
|
| c) Điểm cực tiểu của đồ thị hàm số đã cho là (3;−2). |
|
| d) Với −1<m<1 thì phương trình f(x)=m có 4 nghiệm phân biệt. |
|
Một bể chứa 2 m3 nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ không đổi với tốc độ 20 lít/phút. Biết rằng nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số f(t), thời gian t tính bằng phút. Biết rằng tiệm cận ngang của đồ thị hàm số y=f(t) là y=10. Tính nồng độ muối trong bể sau khi bơm được 1 giờ. (làm tròn kết quả đến hàng phần trăm, đơn vị gam/lít)
Trả lời:
Biết thể tích V (đơn vị: centimét khối) của 1 kg nước tại nhiệt độ T, (0∘C ≤T≤30∘C) được tính bởi công thức: V(T)=999,87−0,06426T+0,0085043T2−0,0000679T3. Thể tích V(T) thấp nhất ở nhiệt độ bao nhiêu? (làm tròn đến hàng đơn vị của đơn vị ∘C)
Trả lời:
Một chất điểm chuyển động theo quy luật và quãng đường di chuyển được sau t giây được tính theo công thức S(t)=−3t3+243t2 (m). Vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu giây?
Trả lời:
Một hãng dược phẩm dùng những chiếc lọ bằng nhựa có dạng hình trụ để đựng thuốc. Biết rằng mỗi lọ có thể tích là 16π cm3 và bề dày không đáng kể. Tính bán kính đáy R, đơn vị cm của lọ để tốn ít nguyên liệu sản xuất lọ nhất (kể cả nắp lọ).
Trả lời:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau:
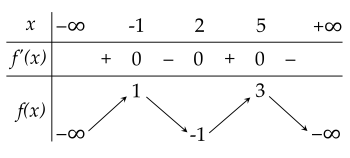
Phương trình f′[5−3f(x)]=0 có bao nhiêu nghiệm thực?
Trả lời:
Cho hàm số y=f′(x) có đồ thị như hình vẽ.
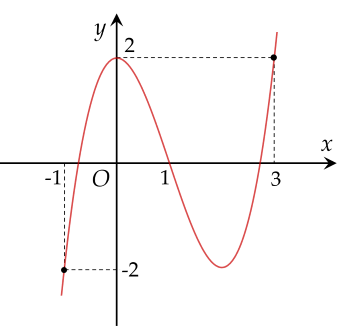
Hàm số y=f(x)−21(x−1)2 nghịch biến trên khoảng (−∞;a). Tìm giá trị nguyên lớn nhất của a.
Trả lời:
