Đề ôn tập và kiểm tra giữa học kì I toán 12 cấu trúc mới mới nhất

Câu 1 (1đ):

Hàm số $y=\dfrac{x}{x^2+1}$ đồng biến trên mỗi khoảng nào dưới đây?

(0;\,+\infty)

.

(-\infty ;\,-1)

và

(1;\,+\infty)

.

(-1;\,1)

.

(-\infty ;\,+\infty )

.

Câu 2 (1đ):

Cho hàm số $y = f(x)$ có đạo hàm $f'(x)=x.(x-1)^2$ , $\forall x\in \mathbb{R}$ . Số điểm cực trị của hàm số đã cho là

0

.

3

.

2

.

1

.

Câu 3 (1đ):

Cho hàm số $y=f\left( x \right)$ có bảng xét dấu đạo hàm như sau.

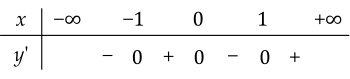
loading...

Mệnh đề nào sau đây đúng?

\underset{\left( -1;\,+\infty \right)}{\mathop{\min }}\,f\left( x \right)=f\left( 0 \right)

.

\underset{\left( 0;\,+\infty \right)}{\mathop{\max}}\,f\left( x \right)=f\left( 1 \right)

.

\underset{\left( -\infty ;\,-1 \right)}{\mathop{\min }}\,f\left( x \right)=f\left( -1 \right)

.

\underset{\left( -1;\,1 \right]}{\mathop{\max}}\,f\left( x \right)=f\left( 0 \right)

.

Câu 4 (1đ):

Cho hàm số $y=f(x )$ có $\underset{x\to +\infty }{\mathop{\lim }}\,f(x )=2$ , $\underset{x\to -\infty }{\mathop{\lim }}\,f(x )=+\infty$ . Khẳng định nào sau đây đúng?

A

Đồ thị hàm số đã cho có một tiệm cận ngang.

B

Đồ thị hàm số đã cho không có tiệm cận ngang

C

Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng

x=2

.

D

Đồ thị hàm số đã cho có hai tiệm cận ngang phân biệt.

Câu 5 (1đ):

Câu 6 (1đ):

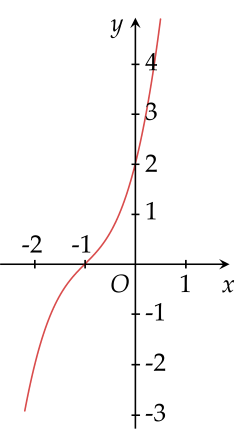
Đường cong ở hình dưới là đồ thị của hàm số nào?

loading...

y=x^{3}+3 x^{2}+4 x+2

.

y=x^{3}+3 x^{2}-4 x+2

.

y=-x^{3}-4 x^{2}-x+2

.

y=x^{3}+x^{2}+2 x+2

.

Câu 7 (1đ):

Cho hình hộp $ABCD.{A}'{B}'{C}'{D}'$ , có đáy $ABCD$ hình bình hành tâm $O$ .

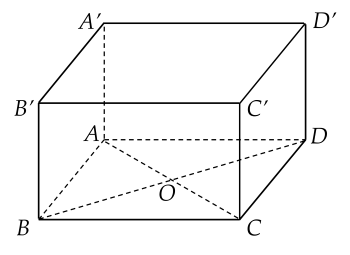
loading...

Khi đó $2\overrightarrow{AO}$ bằng vectơ nào dưới đây?

\overrightarrow{{A}'C}

.

\overrightarrow{AC}

.

\overrightarrow{AD}

.

\overrightarrow{AB}

.

Câu 8 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho hình chữ nhật $OKMN$ .

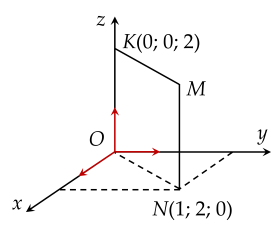
loading...

Tọa độ đỉnh $M$ của hình chữ nhật là

M\left( -1;-\,2;\,-2 \right)

.

M\left( 1;\,2;\,2 \right)

.

M\left( 0;\,2;\,2 \right)

.

M\left( 1;2;\,0 \right)

.

Câu 9 (1đ):

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{u}=(1 ; 1 ; 0)$ và $\overrightarrow{v}=(2 ; 0 ;-1)$ . Độ dài $|\overrightarrow{u}+2 \overrightarrow{v}|$ bằng

\sqrt{30}

.

2 \sqrt{2}

.

2 .

\sqrt{22}

.

Câu 10 (1đ):

Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=2\sin x$ trên đoạn $\Big[ -\dfrac{\pi }{6};\dfrac{5\pi }{6} \Big]$ . Tích $m.M$ bằng

-2

.

2

.

4

.

-\dfrac12

.

Câu 11 (1đ):

Cho ba hàm số: $y=\dfrac{2x+1}{x-3}; \, y=\dfrac{-x+1}{x+3}$ và $y=\dfrac{2x}{3x+2}$ . Có bao nhiêu hàm số mà đồ thị hàm số có tiệm cận ngang là đường thẳng $y=2$ ?

3

.

2

.

0

.

1

.

Câu 12 (1đ):

Gọi $M$ , $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\dfrac{x^2+5}{x-2}$ trên $\left[ -2;1 \right]$ . Giá trị của $M+2m$ bằng

-10

.

-14

.

-8

.

-2

.

Câu 13 (1đ):

Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau.

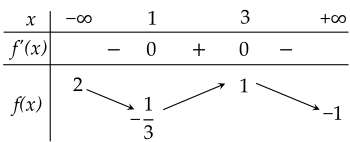
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số có giá trị cực đại bằng $3$ .
b) Hàm số có hai điểm cực trị.
c) Hàm số có giá trị lớn nhất bằng $1$ , nhỏ nhất bằng $-\dfrac{1}{3}$ .
d) Đồ thị hàm số không cắt trục hoành.

Câu 14 (1đ):

Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:

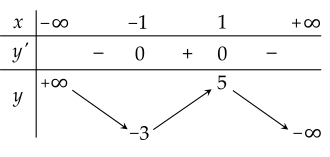
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Phương trình $2f(x)=5$ có $3$ nghiệm.
b) Hàm số đồng biến trên khoảng $(-3 ; 5)$ .
c) Giá trị lớn nhất của hàm số trên $[-1 ; 2]$ bằng $1$ .
d) Hàm số đã cho có $2$ cực trị.

Câu 15 (1đ):

Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng $288$ m $^3$ . Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là $500\,000$ đồng/m $^2$ . Ba kích thước của bể được mô tả như hình vẽ dưới ( $a$ (m) $>0$ ; $c$ (m) $>0$ ).

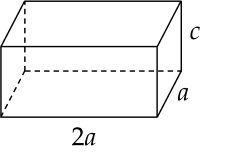
loading...

Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất (Biết độ dày thành bể và đáy bể không đáng kể).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Diện tích các mặt cần xây là $S=2a^2+6ac$ m $^2$ .
b) $2a^2c=280$ .
c) Diện tích các mặt cần xây nhỏ nhất là $216$ m $^2$ .
d) Chi phí thấp nhất để xây dựng bể đó là $108$ triệu đồng.

Câu 16 (1đ):

Một vật nặng $O$ được kéo từ ba hướng như hình vẽ và chịu tác dụng của ba lực $\overrightarrow{F_1},\,\overrightarrow{F_2},\,\overrightarrow{F_3}$ , có độ lớn lần lượt là $24$ N, $12$ N, $6$ N. Biết góc tạo bởi hai lực $\overrightarrow{F_1},\,\overrightarrow{F_2}$ là $120^\circ$ và lực thứ ba vuông góc với hai lực đầu tiên.

loading...

Trong đó điểm $D$ là đỉnh của hình bình hành $OBDA$ và $E$ là đỉnh của hình bình hành $OCED$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{BO}+\overrightarrow{BA}=\overrightarrow{BD}$ .
b) $\overrightarrow{OE}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ .
c) Độ dài vectơ $\overrightarrow{OD}$ là $12\sqrt{7}$ .
d) Độ lớn hợp lực tác dụng vào vật $O$ là $6\sqrt{13}$ N.

Câu 17 (1đ):

Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức $G(x)=0,024x^2(30-x)$ , trong đó $x$ là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp ( $x$ được tính bằng mg). Tìm lượng thuốc $x$ tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.

Trả lời:

Câu 18 (1đ):

Cho một tấm nhôm hình vuông có cạnh $24$ cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x$ (cm), rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một khối hộp chữ nhật không nắp.

loading...

Tìm $x$ (đơn vị cm) sao cho thể tích khối hộp lớn nhất.

Trả lời:

Câu 19 (1đ):

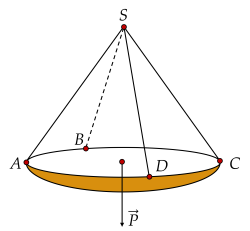
loading...

Một chiếc đèn chùm treo có khối lượng $m=7$ kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích $S A,\, S B,\, S C,\, S D$ sao cho $S . A B C D$ là hình chóp tứ giác đều có $\widehat{A S C}=50^{\circ}$ . Tính độ lớn của lực căng cho mỗi sợi xích khi đèn đứng yên. (Làm tròn kết quả đến chữ số thập phân thứ nhất, đơn vị N)

Trả lời:

Câu 20 (1đ):

Một bể chứa $2$ m $^3$ nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ không đổi với tốc độ $20$ lít/phút. Biết rằng nồng độ muối trong bể sau $t$ phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số $f(t )$ , thời gian $t$ tính bằng phút. Biết rằng tiệm cận ngang của đồ thị hàm số $y = f(t)$ là $y=10$ . Tính nồng độ muối trong bể sau khi bơm được $1$ giờ. (làm tròn kết quả đến hàng phần trăm, đơn vị gam/lít)

Trả lời:

Câu 21 (1đ):

Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}$ và có bảng biến thiên như sau:

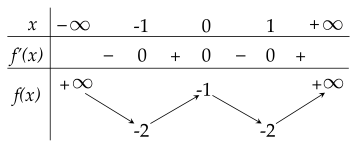
loading...

Hàm số $y = g(x)=f^3(x^3+3x)+2 \, 024$ có bao nhiêu điểm cực tiểu?

Trả lời:

Câu 22 (1đ):

Tìm giá trị lớn nhất của tham số thực $m$ để hàm số $y=\dfrac{x^{3} }{3} -x^{2} -mx+1$ đồng biến trên tập xác định.

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP