Đề thi giữa học kì I toán 10 Kết nối tri thức cấu trúc mới

Câu 1 (1đ):

Cho mệnh đề chứa biến $P(x)$ : " $x^2-5x+4=0$ ". Mệnh đề nào sau đây đúng?

P(5 )

.

P(1 )

.

P(7 )

.

P(6 )

.

Câu 2 (1đ):

Mệnh đề

A

đúng thì mệnh đề phủ định

\overline{A}

sai. Ngược lại, mệnh đề

A

sai thì mệnh đề phủ định

\overline{A}

đúng.

Cho hai mệnh đề: $P$ : " $30$ không chia hết cho $5$ " và $Q$ : " $\pi < 3,15$ ". Khẳng định nào sau đây đúng?

\overline{P}

đúng,

\overline{Q}

sai.

\overline{P}

sai,

\overline{Q}

đúng.

\overline{P}

đúng,

\overline{Q}

đúng.

\overline{P}

sai,

\overline{Q}

sai.

Câu 3 (1đ):

Cho hai tập hợp $A$ và $B$ được minh họa bằng biểu đồ Ven như hình vẽ:

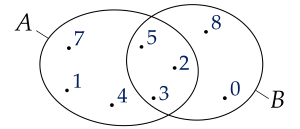
loading...

Khi đó tập hợp $C = A\cup B$ là

\left\{ 1;\,4;\,7 \right\}

.

\left\{ 0;\,1;\,2;\,3;\,4;\,5;\,7;\,8 \right\}

.

\left\{ 0;\,8 \right\}

.

\left\{ 2;\,3;\,5 \right\}

.

Câu 4 (1đ):

Cặp số $(2;3)$ là nghiệm của bất phương trình nào sau đây?

x-3y+7<0

.

2x-3x-1>0

.

x-y<0

.

4x>3y

.

Câu 5 (1đ):

Hệ bất phương trình nào sau đây không là hệ bất phương trình bậc nhất hai ẩn?

\left\{ \begin{aligned} & x+y-6>0 \\ & x \ge 0 \\ & y\ge 0 \\ & 3x+y \le 6 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x<0 \\ & x+y \le \dfrac32 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & -2x + y > 3^2 \\ & x + 4^2y \le 1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x \ge 1 \\ & 2x - xy\ge 0 \\ \end{aligned} \right.

.

Câu 6 (1đ):

Trên nửa đường tròn đơn vị, cho góc $\alpha$ như hình vẽ:

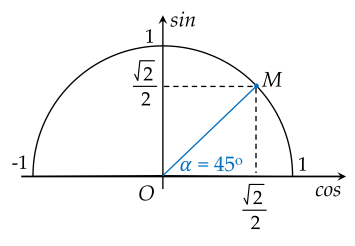
loading...

Các giá trị lượng giác của góc $\alpha$ là

\sin \alpha =-\dfrac{\sqrt2}2

;

\cos \alpha =-\dfrac{\sqrt2}2

;

\tan \alpha =1

;

\cot \alpha =1

.

\sin \alpha =\dfrac{\sqrt2}2

;

\cos \alpha =\dfrac{\sqrt2}2

;

\tan \alpha =1

;

\cot \alpha =1

.

\sin \alpha =\dfrac{\sqrt2}2

;

\cos \alpha =-\dfrac{\sqrt2}2

;

\tan \alpha =1

;

\cot \alpha

không xác định.

\sin \alpha =\dfrac{\sqrt2}2

;

\cos \alpha =\dfrac{\sqrt2}2

;

\tan \alpha =1

;

\cot \alpha =1

.

Câu 7 (1đ):

Cho tam giác $ABC$ có $AB=5,$ $\widehat{B}=60^\circ$ , $\widehat{C}=45^\circ$ . Độ dài cạnh $AC$ là

5\sqrt{3}.

5\sqrt{2}.

\dfrac{5\sqrt{6}}{2}.

10.

Câu 8 (1đ):

Cho tam giác $ABC$ với $BC=7$ cm, $AC=9$ cm, $AB=4$ cm. Giá trị $\cos A$ bằng

\dfrac{1}{3}

.

\dfrac{1}{2}

.

\dfrac{2}{3}

.

-\dfrac{2}{3}

.

Câu 9 (1đ):

Cho hai tập hợp $A=\Big\{ x \in \mathbb{R}\, \big| \, (2x-x^2)(x-1)=0 \Big\}$ , $B=\Big\{ n \in \mathbb{N} \, \big| \,0<n^2<10 \Big\}$ . Mệnh đề nào sau đây đúng?

A \cap B=\left\{ 1;2 \right\}

.

A \cap B=\left\{ 0;3 \right\}

.

A \cap B=\left\{ 2 \right\}

.

A \cap B=\left\{ 0;1;2;3 \right\}

.

Câu 10 (1đ):

Phần không tô màu trong hình vẽ biểu diễn miền nghiệm của hệ bất phương trình nào dưới đây?

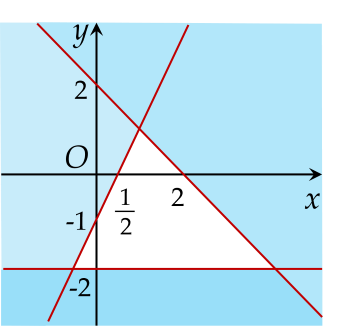
loading...

\left\{ \begin{aligned} & 2x-y<1 \\ & x+y<2 \\ & 3y-x>0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & 2x-y<1 \\ & x+y\ge 2 \\ & y\ge -2 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & 2x-y\ge 1 \\ & x+y\le 2 \\ & y\ge -2 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & 2x-y\ge 1 \\ & 2x+y>2 \\ & 3y-x>0 \\ \end{aligned} \right.

.

Câu 11 (1đ):

Biểu thức $f(x)=3\big(\sin^4 x+\cos^4 x\big)-2\big(\sin^6 x+\cos^6 x\big)$ có giá trị bằng

-3

.

0

.

1

.

2

.

Câu 12 (1đ):

Cho biết $\cos \alpha =-\dfrac23.$ Giá trị của $P=\dfrac{\cot \alpha +3\tan \alpha }{2\cot \alpha +\tan \alpha }$ bằng

-\dfrac{19}{13}.

\dfrac{25}{13}.

\dfrac{19}{13}.

-\dfrac{25}{13}.

Câu 13 (1đ):

Cho hai tập hợp $A=\big\{ x\in \mathbb{R} \, \big| \, x+3<4+2x \big\}$ , $B=\big\{ x\in \mathbb{R} \, \big| \, 5x-3<4x-1 \big\}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $A=\left(-1;\,+\infty \right).$
b) $B=\left(-\infty ;\,2 \right].$
c) $A \cap B=\left(-1;\,2 \right)$ .
d) Tập tất cả các số tự nhiên thuộc cả hai tập $A$ và $B$ là $\left\{ 0;1 \right\}.$

Câu 14 (1đ):

Đô thích ăn hai loại trái cây là cam và xoài, mỗi tuần mẹ cho Đô $200$ nghìn đồng để mua trái cây. Biết rằng giá cam là $15$ $000$ đồng/ $1$ kg, giá xoài là $30$ $000$ đồng/ $1$ kg. Gọi $x, \, y$ (với $a > 0; \, y > 0$ ) lần lượt là số ki-lô-gam cam và xoài mà Đô có thể mua về sử dụng trong một tuần.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Trong tuần, số tiền Đô có thể mua cam là $15 \, 000x$ đồng, số tiền An có thể mua xoài là $30 \, 000y$ đồng.
b) $3x+6y \ge 40$ .
c) Đô không thể mua đủ $5$ kg cam, $4$ kg xoài sử dụng trong tuần.
d) Đô có thể mua $4$ kg cam, $6$ kg xoài sử dụng trong tuần.

Câu 15 (1đ):

Cho hệ bất phương trình $\left\{ \begin{aligned}& 3x+2y\ge 9 \\& x-2y\le 3 \\ & x+y\le 6 \\ & x\quad \ge 1 \\ \end{aligned} \right.$ (I).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Miền nghiệm của hệ bất phương trình (I) là một miền tam giác.
b) $(3;2)$ là một nghiệm của hệ bất phương trình (I).
c) $x=1; \, y=3$ là nghiệm của hệ bất phương trình (I) thỏa mãn $F=3x-y$ đạt giá trị lớn nhất.
d) $x=1; \, y=5$ là nghiệm của hệ bất phương trình (I) thỏa mãn $F=3x-y$ đạt giá trị nhỏ nhất.

Câu 16 (1đ):

Cho $\sin \alpha =\dfrac{12}{13}$ , với $0^\circ <\alpha < 90^\circ$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\cos \alpha <0$ .
b) $\cos \alpha =\sqrt{1-\sin^2 \alpha}$ .
c) $\tan \alpha =-\dfrac{12}{5}$ .
d) $\cot \alpha =-\dfrac{5}{12}$ .

Câu 17 (1đ):

Một lớp học có $25$ học sinh giỏi môn Toán, $23$ học sinh giỏi môn Lí, $14$ học sinh giỏi cả môn Toán và Lí và có $6$ học sinh không giỏi môn nào cả. Lớp học đó có bao nhiêu học sinh?

Trả lời:

Câu 18 (1đ):

Cho tam giác $ABC$ có $A(0;3); \, B(-1;2); \, C(2;1)$ . Có bao nhiêu giá trị nguyên của tham số $m$ để điểm $M\Big(m;\dfrac{2m-1}{2}\Big)$ nằm bên trong tam giác $ABC$ ?

Trả lời:

Câu 19 (1đ):

Một nhà máy sản xuất hai sản phẩm $A$ và $B$ . Biết để sản xuất ra một kg sản phẩm $A$ cần $5$ kg nguyên liệu $I$ và $4$ kg nguyên liệu $II$ ; để sản xuất hai kg sản phẩm $B$ cần $4$ kg nguyên liệu $I$ và $4$ kg nguyên liệu $II$ . Biết giá của mỗi kg nguyên liệu $I$ là $1$ triệu đồng, giá của mỗi kg nguyên liệu $II$ là $2$ triệu đồng. Giá bán của $1$ kg sản phẩm $A$ là $18$ triệu đồng và giá $1$ kg sản phẩm $B$ là $8,25$ triệu đồng. Biết chi phí vận chuyển là $20$ triệu đồng và nhà máy hiện chỉ có $175$ kg nguyên liệu $I$ ; $150$ kg nguyên liệu $II$ . Nhà máy phải sản xuất bao nhiêu sản phẩm $A$ để thu được lợi nhuận lớn nhất?

Trả lời:

Câu 20 (1đ):

Hai chiếc tàu thuỷ cùng xuất phát từ vị trí $A$ , đi thẳng theo hai hướng tạo với nhau một góc $60^\circ$ . Tàu thứ nhất chạy với tốc độ $30$ km/h, tàu thứ hai chạy với tốc độ $40$ km/h. Sau $2$ giờ hai tàu cách nhau bao nhiêu km? (làm tròn kết quả đến chữ số hàng phần mười)

Trả lời:

Câu 21 (1đ):

Cho tam giác nhọn $ABC$ có $a=3, \, b=4$ và diện tích $S=3\sqrt{3}$ . Bán kính $R$ của đường tròn ngoại tiếp tam giác có dạng $R=\dfrac{\sqrt{a}}{b}$ , với $m, \, n\in \mathbb{N}, \, b\lt 5$ . Tính giá trị của biểu thức $T=m+n$ .

Trả lời:

Câu 22 (1đ):

Cho hai số thực $x, \, y$ thỏa mãn $\left\{ \begin{aligned} & x-y\le 2 \\ & x+2y\le 8 \\ & 5x+y\ge 4 \\ \end{aligned} \right.$ . Tìm giá trị lớn nhất của biểu thức $P=2x+3y$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP