Đề kiểm tra giữa học kì I toán 12 cấu trúc mới mới nhất

Câu 1 (1đ):

Cho hai vectơ $\overrightarrow{u},\overrightarrow{v}$ có $| \overrightarrow{u} |=3,\,| \overrightarrow{v} |=4$ và góc giữa hai vectơ $\overrightarrow{u},\overrightarrow{v}$ bằng $60^\circ$ . Tích vô hướng $\overrightarrow{u}.\overrightarrow{v}$ bằng

-6

.

-12

.

6

.

12

.

Câu 2 (1đ):

Trong không gian $Oxyz$ , gọi $M'$ là hình chiếu vuông góc của điểm $M\left(2;\,3;\,-1 \right)$ trên trục $Oy$ thì tọa độ $\overrightarrow{MM'}$ là

\left(0;\,3;\,0 \right).

\left(0;\,2;\,3 \right)

.

\left(-2;\,0;\,1 \right).

\left(3;\,0;\,0 \right).

Câu 3 (1đ):

Cho hàm số $y = f(x)$ có đạo hàm $f'(x)=x-1, \, \forall x\in \mathbb{R}$ . Số điểm cực trị của hàm số đã cho là

0

.

1

.

2

.

3

.

Câu 4 (1đ):

Cho hàm số $y=f'(x)$ có bảng xét dấu như sau:

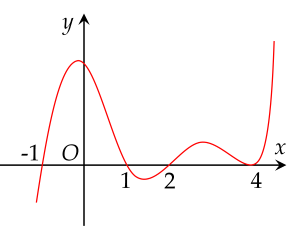
loading...

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

\left(1;+\infty \right)

.

\left(-\infty ; -1 \right)

.

\left(-1 ; +\infty \right)

.

\left(-\infty ; 1 \right)

.

Câu 5 (1đ):

Giá trị lớn nhất của hàm số $y=x^3-\dfrac32x^2+1$ trên khoảng $\Big( -25;\dfrac{11}{10} \Big)$ là

\dfrac{1}{2}

.

0

.

\dfrac{129}{250}

.

1

.

Câu 6 (1đ):

Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?

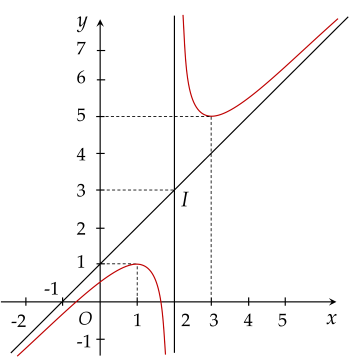
loading...

y=-{{x}^{3}}+3{{x}^{2}}-1

.

y={{x}^{3}}-3{{x}^{2}}-1

.

y={{x}^{4}}-2{{x}^{2}}-1

.

y=-{{x}^{4}}+2{{x}^{2}}-1

.

Câu 7 (1đ):

Điểm nào sau đây thuộc đồ thị của hàm số $y=x^4-3x^2-5$ ?

Điểm

P(1;3)

.

Điểm

M(-1;-3)

.

Điểm

N(2;-1)

.

Điểm

Q(-2;-9)

.

Câu 8 (1đ):

Câu 9 (1đ):

Một công ty sản xuất máy tính đã xác định được rằng, tính trung bình một nhân viên có thể lắp ráp được $N(x)=\dfrac{50x}{x+4}\text{ }\left(x\ge 0 \right)$ bộ phận mỗi ngày sau $x$ ngày đào tạo. Xem $y=N\left(x \right)$ là một hàm số xác định trên $\left[ 0;+\infty \right)$ , khi đó tiệm cận ngang của đồ thị hàm số là

x=50

.

y=50

.

x=\dfrac{25}{2}

.

y=\dfrac{25}{2}

.

Câu 10 (1đ):

Trong không gian cho điểm $O$ và bốn điểm $A, \, B, \, C, \, D$ không có ba điểm nào thẳng hàng. Điều kiện cần và đủ để $A, \, B, \, C, \, D$ tạo thành hình bình hành là

\overrightarrow{O A}+\dfrac{1}{2} \overrightarrow{O B}=\overrightarrow{O C}+\dfrac{1}{2} \overrightarrow{O D}

.

\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}+\overrightarrow{O D}=\overrightarrow{0}

.

\overrightarrow{O A}+\overrightarrow{O C}=\overrightarrow{O B}+\overrightarrow{O D}

.

\overrightarrow{O A}+\dfrac{1}{2} \overrightarrow{O C}=\overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O D}

.

Câu 11 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho $A(1 ; 1 ; 2), \, B(2 ;-1 ; 1)$ và $C(3 ; 2 ;-3)$ . Để $ABCD$ là hình bình hành thì tọa độ điểm $D$ là

(4 ; 0 ;-4)

.

(4 ; 2 ;-4)

.

(0 ;-2 ; 6)

.

(2 ; 4 ;-2)

.

Câu 12 (1đ):

Một hợp tác xã nuôi cá thí nghiệm trong hồ. Người ta thấy rằng nếu trên mỗi đơn vị diện tích của mặt hồ có $n$ con cá thì trung bình mỗi con cá sau một vụ cân nặng $P(n) = 480 – 20n$ (gam). Hỏi phải thả số lượng cá trên một đơn vị diện tích của mặt hồ thuộc khoảng nào dưới đây để cân nặng trung bình của số cá đó tăng?

(0;\,12)

.

(0;\,30)

.

(0;\,20)

.

(12;\,50)

.

Câu 13 (1đ):

Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ cạnh $a$ .

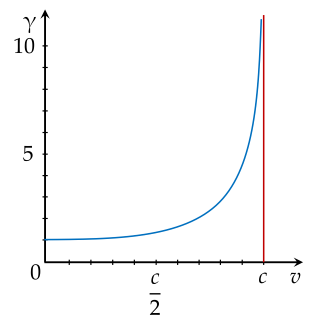
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{DC'}=\overrightarrow{DC}+\overrightarrow{DD'}$ .
b) $\overrightarrow{AD'}.\overrightarrow{CC'}=a^2$ .
c) Gọi $M$ là giao điểm của $CD'$ và $C'D$ . Khi đó, $\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AA'}$ .
d) Góc giữa $A'C$ và $BD$ là $60^\circ$ .

Câu 14 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ:

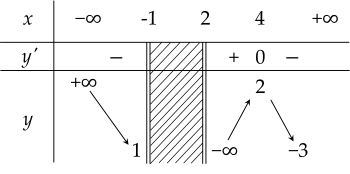
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đồ thị hàm số có đường tiệm cận đứng $x=2$ .
b) Hàm số có đúng $1$ điểm cực trị.
c) Hàm số đạt giá trị lớn nhất là $2$ tại $x=4$ .
d) Hàm số đồng biến trên khoảng $\left( 2;3 \right)$ .

Câu 15 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

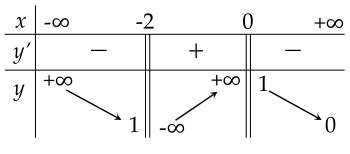
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số đã cho đồng biến trên $\mathbb{R}$ .
b) Phương trình $y=0$ có $3$ nghiệm phân biệt.
c) Hàm số đã cho không có cực trị.
d) Số đường tiệm cận của đồ thị hàm số là $3$ .

Câu 16 (1đ):

Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong $t$ giờ được cho bởi hàm số có công thức $c(t)=\dfrac{t}{t^2+1}$ $\left( mg/L \right)$ . Khi đó

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Nồng độ thuốc trong máu của bện nhân sau $3$ giờ là $c(3)=\dfrac{3}{10}\left( mg/L \right)$ .
b) Đạo hàm của hàm số $c(t)=\dfrac{t}{t^2+1}$ là $c'(t)=\dfrac{1-t^2}{(t^2+1)^2}$ .
c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng $t\in (0;\,2)$ .
d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi $t=\dfrac{1}{2}$ .

Câu 17 (1đ):

Nếu một vật có khối lượng $m$ (kg) thì lực hấp dẫn $\overrightarrow{P}$ (N) của Trái Đất tác dụng lên vật được xác định theo công thức: $\overrightarrow{P}=m . \overrightarrow{g}$ , trong đó $\overrightarrow{g}$ là gia tốc rơi tự do có độ lớn $g=9,8$ m/s $^2$ . Một con khỉ có cân nặng $5$ kg đang biểu diễn xiếc. Nó nắm tay vào dây để treo mình đứng yên như hình vẽ.

loading...

Khi dây ở vị trí cân bằng, tính độ lớn của lực căng dây $\overrightarrow{T_1}$ , đơn vị N (làm tròn kết quả đến chữ số thập phân thứ nhất)

Trả lời:

Câu 18 (1đ):

Gọi $M, \, N$ lần lượt là trung điểm của các cạnh $AC$ và $BD$ của tứ diện $ABCD$ . Gọi $I$ là trung điểm đoạn $MN$ và $P$ là điểm bất kì trong không gian. Tìm giá trị $k$ trong đẳng thức vectơ $\overrightarrow{P I}=k(\overrightarrow{P A}+\overrightarrow{P B}+\overrightarrow{P C}+\overrightarrow{PD})$ . (Ghi kết quả dưới dạng số thập phân)

Trả lời:

Câu 19 (1đ):

Theo thống kê tại một nhà máy $Z$ , nếu áp dụng tuần làm việc $40$ giờ thì mỗi tuần có $100$ công nhân đi làm và mỗi công nhân làm được $120$ sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm $2$ giờ mỗi tuần thì sẽ có $1$ công nhân nghỉ việc và năng suất lao động giảm $5$ sản phẩm/ $1$ công nhân/ $1$ giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là $P\left( x \right)=\dfrac{95{{x}^{2}}+120x}{4}$ , với $x$ là thời gian làm việc trong một tuần (đơn vị: giờ). Nhà máy cần áp dụng thời gian làm việc mỗi tuần mấy giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?

Trả lời: giờ.

Câu 20 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ.

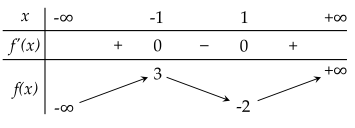
loading...

Phương trình $| f(x) |=2$ có bao nhiêu nghiệm phân biệt?

Trả lời:

Câu 21 (1đ):

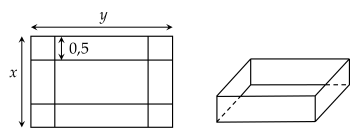
Từ một tấm tôn hình chữ nhật có các kích thước là $x\,\left(m \right)$ , $y\,\left(m \right)$ với $x>1$ và $y>1$ và diện tích bằng $4\text{m}^2$ , người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một cái thùng dạng hình hộp chữ nhật không nắp (như hình vẽ) có chiều cao bằng $0,5$ m. Thể tích của thùng là hàm số $V\left(x \right)$ trên khoảng $\left(1;+\infty \right)$ . Đồ thị hàm số $y=\dfrac{1}{V\left(x \right)}$ có bao nhiêu đường tiệm cận đứng?

Trả lời:

loading...

Câu 22 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ.

loading...

Một hàm số $y = g(x)$ khác xác định theo $f(x)$ có đạo hàm ${g}'(x)=f(x)+2m-1$ . Có bao nhiêu giá trị nguyên của tham số $m$ trên $\left(-10;10 \right)$ để hàm số $y = g(x)$ có đúng hai điểm cực trị?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP