Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 2) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hình hộp ABCD.A′B′C′D′, có đáy ABCD hình bình hành tâm O.
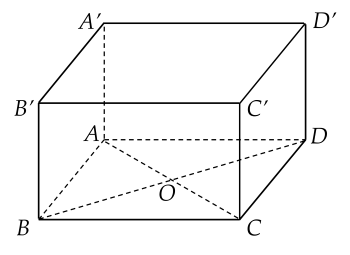
Khi đó 2AO bằng vectơ nào dưới đây?
Số điểm cực trị của hàm số y=2x4−4x2+2024 là
Cho hàm số y=f(x) có bảng biến thiên như sau:
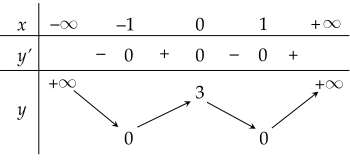
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x)=1+2x8+x trên đoạn [1;2] lần lượt là
Đường cong ở hình dưới là đồ thị của hàm số nào?
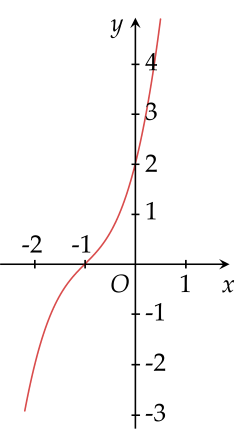
Điểm nào sau đây thuộc đồ thị của hàm số y=x4−3x2−5?
Một ứng dụng của hàm số trong vật lý là hệ số tương đối tính Lorentz được cho bởi công thức γ(v)=1−c2v21, với v là vận tốc tương đối giữa các hệ quy chiếu quán tính, c là tốc độ ánh sáng trong chân không. Hàm này được sử dụng trong thuyết tương đối đặc biệt của Einstein để mô tả các hiệu ứng tương đối tính có đồ thị dưới đây:
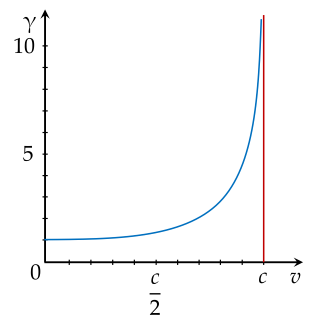
Đồ thị hàm số đó có tiệm cận đứng là
Cho hình chóp S.ABC có SA=1, SB=2, SC=3, ASB=60∘, BSC=90∘,CSA=120∘. Giá trị cos(SA,BC) (làm tròn đến hàng phần trăm) bằng

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;−1), B(2;−1;3), C(−2;3;3). Điểm D(a;b;c) là đỉnh thứ tư của hình bình hành ABCD, khi đó P=a2+b2−c2 có giá trị bằng
Cho hình hộp ABCD.A′B′C′D′. Giá trị của k thích hợp điền vào đẳng thức vectơ AC+BA′+k(DB+C′D)=0 là
Cho hình bình hành ABCD có E là trung điểm của AD, F là trung điểm của BC.
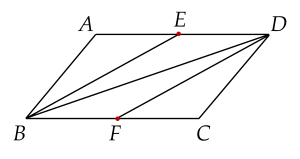
| a) BD=BA+BC |
|
| b) BD=EF |
|
| c) DE=DB−DF |
|
| d) DB=CB+AB |
|
Cho hàm số y=f(x) liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ.
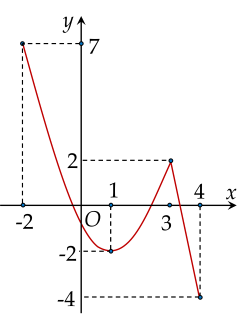
| a) Trên đoạn [−2;4], đồ thị hàm số y=f(x) có 2 điểm cực trị. |
|
| b) Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;2] là −2. |
|
| c) Giá trị lớn nhất của hàm số y=f(x) trên đoạn [1;4] là −4. |
|
| d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;4] là 11. |
|
Cho hàm số y=f(x), có đồ thị như hình vẽ:
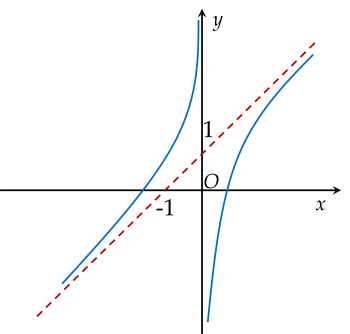
| a) Tiệm cận xiên của đồ thị hàm số y=f(x) là đường thẳng y=x+1. |
|
| b) Tiệm cận đứng của đồ thị hàm số là x=0. |
|
| c) x→+∞limxf(x)=2. |
|
| d) x→+∞lim[f(x)−x]=3. |
|
Một khúc gỗ có dạng hình khối nón có bán kính đáy r=2 m, chiều cao l=6 m. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ.
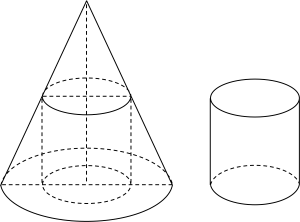
| a) Đặt x là bán kính đáy hình trụ, h là chiều cao của hình trụ. Khi đó chiều cao của khối trụ tính theo bán kính đáy hình trụ là h=−3x+6 (m) với 0<x<2. |
|
| b) Hàm số xác định thể tích của khối trụ trên là V=6x2−3x3 (m3), ∀x∈(0;2). |
|
| c) Giả sử bác thợ mộc chế tác khúc gỗ đó thành hình trụ có bán kính đáy bằng chiều cao, khi đó thể tích của khối trụ là V=827π (m3). |
|
| d) Thể tích lớn nhất của khối gỗ mà bác thợ mộc chế tác là Vmax=932π (m3). |
|
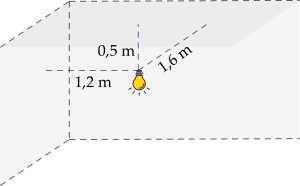
Hình vẽ trên minh hoạ một chiếc đèn được treo cách trần nhà là 0,5 m, cách hai tường lần lượt là 1,2 m và 1,6 m. Hai bức tường vuông góc với nhau và cùng vuông góc với trần nhà. Người ta di chuyển chiếc đèn đó đến vị trí mới cách trần nhà là 0,4 m, cách hai tường đều là 1,5 m. Vị trí mới của bóng đèn cách vị trí ban đầu là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ hai)
Trả lời:
Gọi M,N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm đoạn MN và P là điểm bất kì trong không gian. Tìm giá trị k trong đẳng thức vectơ PI=k(PA+PB+PC+PD). (Ghi kết quả dưới dạng số thập phân)
Trả lời:
Một hãng dược phẩm dùng những chiếc lọ bằng nhựa có dạng hình trụ để đựng thuốc. Biết rằng mỗi lọ có thể tích là 16π cm3 và bề dày không đáng kể. Tính bán kính đáy R, đơn vị cm của lọ để tốn ít nguyên liệu sản xuất lọ nhất (kể cả nắp lọ).
Trả lời:
Cho hàm số y=f(x) thỏa mãn f(x)=4 và có bảng biến thiên như hình dưới:
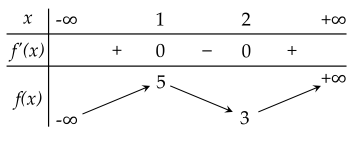
Có bao nhiêu giá trị nguyên của tham số m để đường thẳng y=m cắt đồ thị hàm số y=f(∣x∣) tại 6 điểm phân biệt?
Trả lời:
Một bể chứa 2 m3 nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ không đổi với tốc độ 20 lít/phút. Biết rằng nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số f(t), thời gian t tính bằng phút. Biết rằng tiệm cận ngang của đồ thị hàm số y=f(t) là y=10. Tính nồng độ muối trong bể sau khi bơm được 1 giờ. (làm tròn kết quả đến hàng phần trăm, đơn vị gam/lít)
Trả lời:
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ.
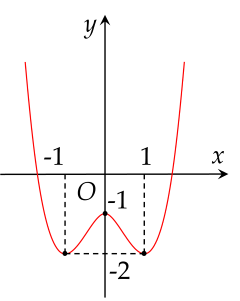
Một hàm số y=g(x) khác xác định theo f(x) có đạo hàm g′(x)=f(x)+2m−1. Có bao nhiêu giá trị nguyên của tham số m trên (−10;10) để hàm số y=g(x) có đúng hai điểm cực trị?
Trả lời:
