Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 2) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=f(x) có đồ thị như hình vẽ:
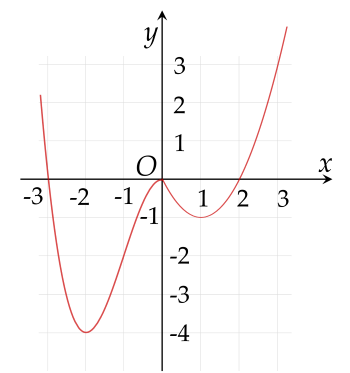
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
Số điểm cực trị của hàm số y=x+12x+3 là
Giá trị nhỏ nhất của hàm số y=x+1x−1 trên đoạn [0;3] là
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ:
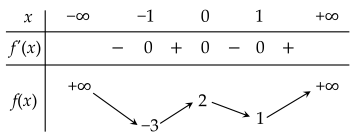
Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−1;2] là
Đồ thị hàm số y=x−1x+2 có bao nhiêu đường tiệm cận?
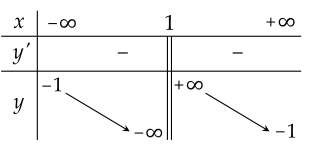
Hàm số nào dưới đây có bảng biến thiên như hình vẽ trên?
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;−1), B(2;−1;3), C(−2;3;3). Điểm D(a;b;c) là đỉnh thứ tư của hình bình hành ABCD, khi đó P=a2+b2−c2 có giá trị bằng
Cho hình chóp S.ABC có SA=1, SB=2, SC=3, ASB=60∘, BSC=90∘,CSA=120∘. Giá trị cos(SA,BC) (làm tròn đến hàng phần trăm) bằng

Cho hàm số y=f(x)=x2+1. Số nghiệm của phương trình f(x+3)=1 là
Cho hàm số y=f(x) liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ.
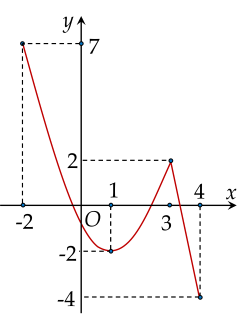
| a) Trên đoạn [−2;4], đồ thị hàm số y=f(x) có 2 điểm cực trị. |
|
| b) Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;2] là −2. |
|
| c) Giá trị lớn nhất của hàm số y=f(x) trên đoạn [1;4] là −4. |
|
| d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;4] là 11. |
|
Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức f(t)=t+526t+10 (với f(t) được tính bằng nghìn người)
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Số dân của thi trấn đó sau 10 năm khoảng 16000 người. |
|
| b) Số dân thị trấn đó vào năm 2025 khoảng 24 nghìn người. |
|
| c) Coi f(t)là một hàm số xác định trên nửa khoảng [0;+∞). Đồ thị hàm số y=f(t)=t+526t+10 có tiệm cận ngang là y=26. |
|
| d) Đạo hàm của hàm số y=f(t) biểu thị tốc độ tăng dân số của thị trấn (tính bằng nghìn người/năm). Vào năm 1990 thì tốc độ tăng dân số là 0,127 nghìn người trên /năm. |
|
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi hàm số có công thức c(t)=t2+1t (mg/L).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Nồng độ thuốc trong máu của bện nhân sau 3 giờ là c(3)=103 (mg/L). |
|
| b) Đạo hàm của hàm số c(t)=t2+1t là c′(t)=(t2+1)21−t2. |
|
| c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng t∈(0;2). |
|
| d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi t=21. |
|
Cho hình lăng trụ tam giác ABC.A′B′C′.
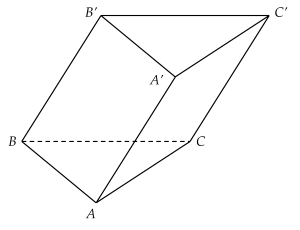
| a) AA′+BB′=2CC′. |
|
| b) AB−CC′−A′B′=BB′. |
|
| c) BB′+2BC+AA′=2BC′. |
|
| d) AB′+BA+2CC′=3BB′. |
|
Từ một tấm tôn hình chữ nhật có các kích thước là x (m), y (m) với x>1 và y>1 và diện tích bằng 4 m2, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một cái thùng dạng hình hộp chữ nhật không nắp (như hình vẽ) có chiều cao bằng 0,5 m.
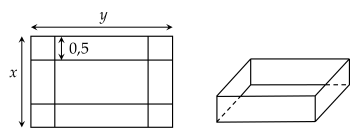
Thể tích của thùng là hàm số V(x) trên khoảng (1;+∞). Đồ thị hàm số y=V(x)1 có bao nhiêu đường tiệm cận đứng?
Trả lời:
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số y=h(x)=−13200001x3+35209x2−4481x+840 với 0≤x≤2000. Biết đỉnh của lát cắt dãy núi nằm ở độ cao h (m) thuộc đoạn [1000;2000]. Tính h. (Kết quả làm tròn đến hàng đơn vị)
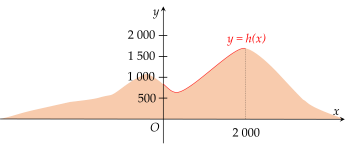
Trả lời:
Cho một tấm nhôm hình vuông có cạnh 24 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một khối hộp chữ nhật không nắp.

Tìm x (đơn vị cm) sao cho thể tích khối hộp lớn nhất.
Trả lời:
Ban đầu bạn An ở vị trí điểm A muốn đến điểm C ở bên bờ sông. Biết rằng An đứng đối diện và cách chiếc cọc tại điểm B một khoảng cách 10 km. Khi sang sông, An sẽ đến vị trí điểm M bất kì thuộc đoạn thẳng BC.
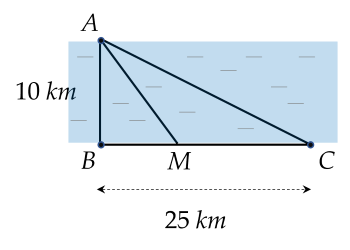
Biết trên sông, An di chuyển với vận tốc 30 km/h và trên đất liền, An di chuyển với vận tốc 50 km/h. Tính 5MB+3MC (đơn vị km) để bạn An đến vị trí điểm C nhanh nhất?
Trả lời:
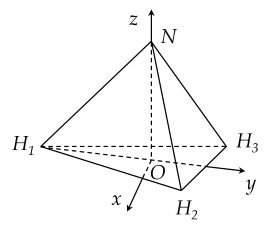
Trong hóa học cấu tạo của phân tử ammoniac (NH3) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen (N) và đáy là tam giác H1H2H3 với H1,H2,H3 là vị trí của ba nguyên tử hydrogen (H). Góc tạo bởi liên kết H−N−H, có hai cạnh là hai đoạn thẳng nối N với hai trong ba điểm H1,H2,H3 (chẳng hạn như H1NH2) , được gọi là góc liên kết của phân tử NH3. Góc này xấp xỉ 120∘. Trong không gian Oxyz, cho một phân tử NH3 được biểu diễn bởi hình chóp tam giác đều N.H1H2H3 với O là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm N thuộc trục Oz, ba nguyên tử hydrogen ở các vị trị H1,H2,H3 trong đó H1(0;−3;0) và H2H3 song song với trục Ox. Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen. (làm tròn kết quả đến hàng phần trăm)
Trả lời:
Nếu một vật có khối lượng m (kg) thì lực hấp dẫn P (N) của Trái Đất tác dụng lên vật được xác định theo công thức: P=m.g, trong đó g là gia tốc rơi tự do có độ lớn g=9,8 m/s2. Một con khỉ có cân nặng 5 kg đang biểu diễn xiếc. Nó nắm tay vào dây để treo mình đứng yên như hình vẽ.

Khi dây ở vị trí cân bằng, tính độ lớn của lực căng dây T1, đơn vị N (làm tròn kết quả đến chữ số thập phân thứ nhất)
Trả lời:
