olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Thông tin của bạn

Đề số 1 - bộ Kết nối tri thức với cuộc sống SVIP

In bài

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Điểm nào sau đây thuộc đồ thị hàm số y=3x2+x+4y=\sqrt{3x^2+x+4}?

(−1;1)\left(-1;1 \right).
(0;2)\left(0;2 \right).
(2;0)\left(2;0 \right).
(1;4)\left(1;4 \right).
Câu 2 (1đ):

Cho (P): y=x2−4x+3\left(P \right): \, y=x^2-4x+3. Mệnh đề nào sau đây đúng?

Hàm số nghịch biến trên (−∞;2)\left(-\infty ;2 \right).
Hàm số đồng biến trên (−∞;4)\left(-\infty ;4 \right).
Hàm số đồng biến trên (−∞;2)\left(-\infty ;2 \right).
Hàm số nghịch biến trên (−∞;4)\left(-\infty ;4 \right).
Câu 3 (1đ):

Số x=1x=1 là nghiệm của tam thức bậc hai nào sau đây?

f(x)=x2+3x+4f\left(x \right)=x^2+3x+4.
f(x)=x2−3x−4f\left(x \right)=x^2-3x-4.
f(x)=−2x2−1f\left(x \right)=-2x^2-1.
f(x)=x2−1f\left(x \right)=x^2-1.
Câu 4 (1đ):

Cho biểu thức f(x)=3x2+2x+1f\left(x \right)=3x^2+2x+1. f(x)>0f\left(x \right)>0 khi

x<0x<0.
x∈Rx\in \mathbb{R}.
x>0x>0.
x≠−2x\ne -2.
Câu 5 (1đ):

Parabol (P): y=ax2+3x−2\left(P \right): \, y=ax^2+3x-2 cắt trục OxOx tại điểm có hoành độ bằng 22. (P)\left(P \right) là đồ thị của hàm số nào sau đây?

y=−x2+x−2.y=-x^2+x-2.
y=−x2+3x−2.y=-x^2+3x-2.
y=x2+3x−2.y=x^2+3x-2.
y=−x2+3x−3.y=-x^2+3x-3.
Câu 6 (1đ):

Tọa độ một vectơ chỉ phương của đường thẳng song song trục OxOx là

(−1;1).(-1;1).
(1;0)\left(1;0 \right).
(0;−1).(0;-1).
(1;1).\left(1;1 \right).
Câu 7 (1đ):

Phương trình tham số của đường thẳng qua A(3;−1)A\left(3;-1 \right) và B(1;5)B\left(1;5 \right) là

{x=3+ty=−1+3t\left\{ \begin{aligned} & x=3+t \\& y=-1+3t \\ \end{aligned} \right..
{x=3−ty=−1−3t\left\{ \begin{aligned}&x=3-t \\&y=-1-3t \\ \end{aligned} \right..
{x=3−ty=−1+3t\left\{ \begin{aligned} &x=3-t \\ &y=-1+3t \\ \end{aligned} \right..
{x=1−ty=5−3t\left\{ \begin{aligned}&x=1-t \\&y=5-3t \\ \end{aligned} \right..
Câu 8 (1đ):

Góc giữa hai đường thẳng 6x−5y+15=06x-5y+15=0 và {x=10−6ty=1+5t\left\{ \begin{aligned}&x=10-6t \\&y=1+5t \\ \end{aligned} \right. bằng

60∘60^\circ.
90∘90^\circ.
45∘45^\circ.
30∘30^\circ.
Câu 9 (1đ):

Cho 2 đường thẳng d1: {x=2+ty=−3+2td_1: \, \left\{ \begin{aligned}& x=2+t \\ & y=-3+2t \\ \end{aligned} \right., d2: {x=5−ty=−7+3td_2: \, \left\{ \begin{aligned} & x=5-t \\ & y=-7+3t \\ \end{aligned} \right.. Khẳng định nào sau đây đúng?

d1d_1 và d2d_2 cắt nhau tại M(3;1)M\left(3;1 \right).
d1d_1 trùng d2d_2.
d1d_1 // d2d_2.
d1d_1 và d2d_2 cắt nhau tại M(1;3)M\left(1;3 \right).
Câu 10 (1đ):

Khoảng cách từ điểm M(2;0)M\left(2;0 \right) đến đường thẳng Δ: {x=1+3ty=2+4t\Delta: \, \left\{ \begin{aligned} & x=1+3t \\ & y=2+4t \\ \end{aligned} \right. bằng

25\dfrac2{5}.
22.
105\dfrac{10}{\sqrt{5}}.
52\dfrac{\sqrt{5}}2.
Câu 11 (1đ):

Phương trình đường tròn (C)\left(C \right) có đường kính ABAB với A(1;1), B(7;5)A\left(1;1 \right), \, B\left(7;5 \right) là

(C): (x−4)2+(y−3)2=13\left(C \right): \, (x-4)^2+(y-3)^2=13.
(C): (x−4)2+(y+3)2=13\left(C \right): \, (x-4)^2+(y+3)^2=13.
(C): (x+4)2+(y−3)2=13\left(C \right): \, (x+4)^2+(y-3)^2=13.
(C): (x+4)2+(y+2)2=13\left(C \right): \, (x+4)^2+(y+2)^2=13.
Câu 12 (1đ):

Tập xác định của hàm số y=x2−4x+25−x2y=\sqrt{{x^2}-4x}+\sqrt{25-x^2} là

(−∞;0]∪[4;+∞)\left(-\infty ;0 \right]\cup \left[ 4;+\infty \right).
[−5;5]\left[ -5;5 \right].
(−5;0)∪(4;5)\left(-5;0 \right)\cup \left(4;5 \right).
[−5;0]∪[4;5]\left[ -5;0 \right] \cup \left[ 4;5 \right].
Câu 13 (1đ):

Cho tam thức bậc hai f(x)=ax2+bx+c (a≠0)f\left(x \right)=a{x^2}+bx+c\,\left(a\ne 0 \right) và Δ=b2−4ac\Delta ={{b}^2}-4ac.

(Nhấp vào dòng để chọn đúng / sai)
f(x)f\left(x \right) luôn cùng dấu với hệ số aa với mọi x∈Rx\in \mathbb{R} khi Δ<0\Delta <0.
Điều kiện để f(x)≤0f\left(x \right)\le 0, ∀x∈R\forall x\in \mathbb{R} là {a<0Δ<0\left\{ \begin{aligned} & a<0 \\ & \Delta <0 \\ \end{aligned} \right..
Với a=1, b=−2a=1, \, b=-2 và c=3 c = 3 thì f(x)≥0f(x)\ge 0 với mọi x∈Rx\in \mathbb{R}.
Với a=1, b=c=4a=1, \, b=c=4 thì f(x)≥0f(x)\ge 0 với mọi x∈Rx\in \mathbb{R}.
Câu 14 (1đ):

Cho đường thẳng d:  {x=−1+2ty=3−5td:\,\,\left\{ \begin{aligned} & x=-1+2t \\ & y=3-5t \\ \end{aligned} \right..

(Nhấp vào dòng để chọn đúng / sai)
Vectơ chỉ phương của dd là u→=(2;−5)\overrightarrow{u}=\left(2;-5 \right).
Vectơ pháp tuyến của ddlà n→=(5;−2)\overrightarrow{n}=\left(5;-2 \right).
Đường thẳng dd đi qua M(−1;2)M\left(-1;2 \right).
Hệ số góc của đường thẳng dd là k=−52k=-\dfrac{5}2.
Câu 15 (1đ):

Cho ba đường thẳng d1: {x=1+ty=−1+2td_1: \, \left\{ \begin{aligned} & x=1+t \\ & y=-1+2t \\ \end{aligned} \right., d2: 3x+5y+7=0,d_2: \, 3x+5y+7=0, d3: −4x+2y+8=0.d_{3}: \, -4x+2y+8=0.

(Nhấp vào dòng để chọn đúng / sai)
d1d_1 // d3d_3.
d1d_1 cắt d2.d_2.
d2⊥d3d_2\perp d_3.
Giao điểm của d2d_2 và d3d_3 là I(−1;2).I\left(-1;2 \right).
Câu 16 (1đ):

Cho bảng số liệu cung cấp giá vé xe buýt giữa các địa điểm:

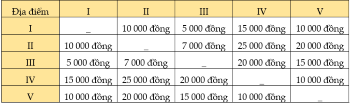
loading...

(Nhấp vào dòng để chọn đúng / sai)
Tuyến II-III có giá vé thấp nhất trong số các tuyến I-V; II-IV; IV-V; II-III.
Hành khách từ địa điểm III đi đến địa điểm II có giá vé thấp nhất?
c) Một du khách đi từ địa điểm I đến địa điểm IV và muốn dừng ở hai địa điểm nữa để tham quan. Trong các lộ trình được gợi ý: (1) I-II-III-IV; (2) I-III-II-IV; (3) I-V-III-IV; (4) I-III-V-IV thì lộ trình (4) sẽ có giá vé thấp nhất cho du khách.
d) Do giá nhiên liệu tăng nên giá vé xe buýt được điều chỉnh tăng thêm 1 000 đồng cho các tuyến có giá dưới 10 000 đồng. So với thời điểm trước khi tăng giá, số vé được bán ra ở mỗi tuyến là không đổi, nếu số vé được bán ra cho tuyến I-III gấp đôi số vé được bán ra cho tuyến II-III thì tổng doanh thu từ hai tuyến này tăng lên 16,67%.
Câu 17 (1đ):

Tập nghiệm của bất phương trình (x2−x+6)2−9(x2−x)−46<0{{\left({x^2}-x+6 \right)}^2}-9\left({x^2}-x \right)-46<0 là khoảng (a;b)\left(a;b \right). Tính b−ab-a.

Đáp án:

Câu 18 (1đ):

Một công ty đồ gia dụng sản xuất bình đựng nước thấy rằng khi đơn giá của bình đựng nước là xx (nghìn đồng) thì doanh thu được biểu diễn theo xx có phương trình T(x)=−560x2+50 000xT\left(x \right)=-560{x^2}+50 \, 000x. Để doanh thu từ việc bán bình đựng nước đạt tối thiểu 11 tỉ đồng thì bình nước có khoảng đơn giá (đơn vị nghìn đồng) là [M;N][M ; N]. Tính M+NM + N.

Đáp án:

Câu 19 (1đ):

Có bao nhiêu giá trị nguyên của tham số mm để bất phương trình −2x2+(m+4)x+m+4≥0-2{x^2}+\left(m+4 \right)x+m+4\ge 0 vô nghiệm?

Đáp án:

Câu 20 (1đ):

Một rạp chiếu phim Đào phở và piano có sức chứa 1 000 người. Với giá vé 40 000 đồng, trung bình sẽ có khoảng 300 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo sát thị trường và thấy rằng nếu giá vé cứ giảm 10 000 đồng trên mỗi vé thì sẽ có thêm 100 người đến rạp mỗi ngày. Tìm mức giá mỗi vé (đơn vị đồng) để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.

Đáp án:

Câu 21 (1đ):

Trong mặt phẳng tọa độ Oxy,Oxy, cho đường tròn (C)(C) có phương trình: x2+y2+211x−25=0,x^2+y^2+2\sqrt{11}x-25=0, đường tròn (C)\left(C \right) cắt tia OyOy tại M.M. Phương trình đường tròn (C1)\left(C_1\right) có bán kính R1=3R_1=3 và tiếp xúc ngoài với (C)\left(C \right) tại MM có tâm I1(a;b)I_1(a ; b). Tính a2+b2a^2+b^2.

Đáp án:

Câu 22 (1đ):

Trong mặt phẳng tọa độ OxyOxy, cho đường thẳng d: ax+by+c=0d: \, ax+by+c=0, (a, b, c∈N, c<10a, \, b, \, c \in \mathbb{N}, \, c<10) vuông góc với Δ: 2x−y+3=0\Delta: \, 2x-y+3=0 và cách điểm M(2;−2)M(2;-2) một khoảng 5\sqrt{5}. Tính T=a+b+cT=a+b+c.

Đáp án:

OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP