Đề ôn tập và kiểm tra giữa học kì I toán 10 mới nhất

Câu 1 (1đ):

Trong tam giác $ABC$ có $\widehat{B}=75^\circ$ , $\widehat{C}=45^\circ$ , $AB=6$ . Độ dài cạnh $BC$ bằng

3\sqrt{2}

.

6\sqrt{3}

.

2\sqrt{3}

.

3\sqrt{6}

.

Câu 2 (1đ):

Khẳng định nào sau đây sai?

\cos 60^\circ=\sin 120^\circ

.

\cos 60^\circ=\sin 30^\circ

.

\sin 60^\circ=-\cos 120^\circ

.

\cos 30^\circ=\sin 120^\circ

.

Câu 3 (1đ):

Cho hệ bất phương trình $\left\{ \begin{aligned} & x+y>0 \\ & 2x+5y<0 \\ \end{aligned} \right.$ có tập nghiệm là $S$ . Khẳng định nào sau đây đúng?

(1;1) \in S

.

\Big(-\dfrac12;\dfrac{2}{5}\Big) \in S

.

(-1;-1) \in S

.

\Big(1;-\dfrac12\Big) \in S

.

Câu 4 (1đ):

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

2x-5y+z\le 0

.

x^2+3x>\dfrac1{3}

.

3x^2+2y \le 5

.

3x<2y-4

.

Câu 5 (1đ):

Cho tập hợp $M=\Big\{x \in \mathbb{R} \, \big| \, x-29<4-2x \Big\}$ . Tập hợp $M$ viết dưới kí hiệu khoảng, nửa khoảng, đoạn là

M=\left(-\infty ; 11 \right]

.

M=\left(-\infty ; 11 \right)

.

M=\left[ -\infty ; 11 \right)

.

M=\left(11 ; +\infty \right)

.

Câu 6 (1đ):

Tập hợp $A=\Big\{\dfrac{1}{2}; \, \dfrac{2}{3}; \, \dfrac{3}{4}; \, \dfrac{4}{5}; \, \dfrac{5}{6}\Big\}$ khi viết bằng cách nêu tính chất đặc trưng của phần tử là

A=\Big\{ \dfrac{n-1}{n} \, \big| \, n \in \mathbb{N}^*, \, n \le 6 \Big\}

.

A=\Big\{ \dfrac{n}{n+1} \, \big| \, n \in \mathbb{N}, \, n \le 5 \Big\}

.

A=\Big\{ \dfrac{n-1}{n} \, \big| \, n \in \mathbb{N}, \, n \le 6 \Big\}

.

A=\Big\{ \dfrac{n}{n+1} \, \big| \, n \in \mathbb{N}^*, \, n \le 5 \Big\}

.

Câu 7 (1đ):

Mệnh đề phủ định của mệnh đề " $9 + \pi \ge 12$ " là

"

9 + \pi < 12

".

"

9 + \pi \le 12

".

"

9 + \pi \ne 12

".

"

9 + \pi > 12

".

Câu 8 (1đ):

Công thức nào sau đây đúng?

S=\dfrac{1}{2}bc\sin B.

S=\dfrac{1}{2}bc\sin A.

S=\dfrac{1}{2}ac\sin A.

S=C\dfrac{1}{2}bc\sin C.

Câu 9 (1đ):

Đẳng thức nào sau đây sai?

\sin 60^\circ +\cos 150^\circ = 0

.

\sin 45^\circ + \sin 45^\circ = \sqrt{2}

.

\sin 120^\circ +\cos 30^\circ = 0

.

\sin 30^\circ + \cos 60^\circ = 1

.

Câu 10 (1đ):

Cho tam giác $ABC$ có trọng tâm $G$ , hai trung tuyến $BM=6$ và $CN=9$ ; $\widehat{BGC}=120^\circ$ . Diện tích tam giác $ABC$ là

S=12\sqrt{3}.

S=18\sqrt{3}.

S=6\sqrt{3}.

S=24

.

Câu 11 (1đ):

Cho $\tan \alpha =2$ . Giá trị của $A=\dfrac{3\sin \alpha +\cos \alpha }{\sin \alpha -\cos \alpha }$ là

\dfrac{7}{3}

.

7

.

\dfrac{5}{3}

.

5

.

Câu 12 (1đ):

Miền nghiệm của bất phương trình sau $x-2y+1<0$ là phần tô màu (không bao gồm đường thẳng nét đứt) trong hình vẽ nào dưới đây?

Câu 13 (1đ):

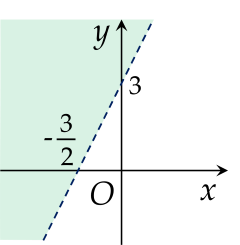
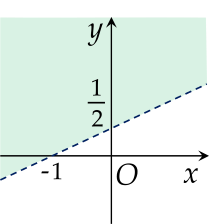
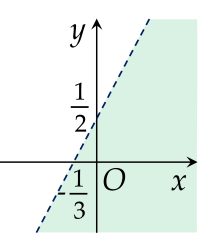
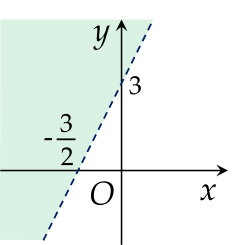
Cho các hệ bất phương trình sau: $\left\{ \begin{aligned} &x-2y \le 0 \\&5x-y \ge -4 \\&x+2y \le 5 \\ \end{aligned} \right.$ , $\left\{ \begin{aligned} &-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\&y\le 6 \\ \end{aligned} \right.$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned} &x-2y\le 0 \\ &5x-y\ge -4 \\ &x+2y\le 5 \\ \end{aligned} \right.$ là miền tam giác.
b) Điểm $M(1;1)$ thỏa mãn miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&x-2y\le 0 \\&5x-y\ge -4 \\&x+2y\le 5 \\ \end{aligned} \right.$ .
c) Miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\&y\le 6 \\ \end{aligned} \right.$ là miền tứ giác.
d) Điểm $O(0;0)$ không thỏa mãn miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\& y\le 6 \\ \end{aligned} \right.$ .

Câu 14 (1đ):

Cho hai tập hợp $A=\big\{ x\in \mathbb{R} \, \big| \, x+3<4+2x \big\}$ , $B=\big\{ x\in \mathbb{R} \, \big| \, 5x-3<4x-1 \big\}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $A=\left(-1;\,+\infty \right).$
b) $B=\left(-\infty ;\,2 \right].$
c) $A \cap B=\left(-1;\,2 \right)$ .
d) Tập tất cả các số tự nhiên thuộc cả hai tập $A$ và $B$ là $\left\{ 0;1 \right\}.$

Câu 15 (1đ):

Cho $P(x)$ : " $x^2-x-2=0$ " với $x$ là các số thực.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $x=0$ thì $P(x)$ là mệnh đề đúng.
b) $P(-1)$ là mệnh đề sai.
c) $P(x)$ luôn là mệnh đề sai với $x$ là các số thực bất kì.
d) $P(2)$ là mệnh đề đúng.

Câu 16 (1đ):

Cho các tập hợp $C_{\mathbb{R}} A=\left[ -3;\sqrt{8} \right)$ , $C_{\mathbb{R}}B=\left(-5;2 \right) \cup \left(\sqrt{3};\sqrt{11} \right).$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $A=\left(-\infty ;\,-3 \right)\cup \left[ \sqrt{8};+\infty \right)$ .
b) $B=\left(-\infty ;-5 \right) \cup \left(\sqrt{11};+\infty \right)$ .
c) $A \cap B=\left(-\infty ;-5 \right) \cup \left[ \sqrt{8};+\infty \right)$ .
d) $C_{\mathbb{R} }\left(A\cap B \right)=\left(-5;\sqrt{11} \right)$ .

Câu 17 (1đ):

Lớp 10A có $21$ em thích học Toán, $19$ em thích học Văn và có $18$ em thích học tiếng Anh. Trong số đó có $9$ em thích học cả Toán lẫn Văn, $7$ em thích học cả Văn lẫn tiếng Anh, $6$ em thích học cả Toán lẫn tiếng Anh và có $4$ em thích học cả ba môn Toán, Văn, Anh, không có em nào không thích một trong ba môn học trên. Trong lớp 10A có bao nhiêu học sinh?

Trả lời:

Câu 18 (1đ):

Cho các tập hợp khác rỗng $A=\Big[ m-1;\dfrac{m+3}{2} \Big]$ và $B=\left(-\infty ;-3 \right)\cup \left[ 3;+\infty \right)$ . Tìm số nguyên $m$ lớn nhất để $A\cap B\ne \varnothing$ .

Trả lời:

Câu 19 (1đ):

Bạn Lan mang theo đúng $15$ nghìn đồng để đi mua vở. Vở loại $A$ có giá $3 \, 000$ đồng một cuốn, vở loại $B$ có giá $4 \, 000$ đồng một cuốn. Bạn Lan có thể mua nhiều nhất bao nhiêu quyển vở sao cho bạn có cả hai loại vở?

Trả lời:

Câu 20 (1đ):

Tìm giá trị nhỏ nhất của biết thức $F=x+y$ trên miền xác định bởi hệ $\left\{ \begin{aligned} & x \ge 0 \\ & 5x-4y \le 10 \\ & 4x+5y \le 10 \\ \end{aligned} \right.$ . (làm tròn kết quả đến chữ số thập phân thứ nhất)

Trả lời:

Câu 21 (1đ):

Trong một cuộc thi pha chế đồ uống gồm hai loại là $A$ và $B$ , mỗi đội chơi được sử dụng tối đa $24$ g hương liệu, $9$ cốc nước lọc và $210$ g đường. Để pha chế một cốc đồ uống loại $A$ cần $1$ cốc nước lọc, $30$ g đường và $1$ g hương liệu. Để pha chế một cốc đồ uống loại $B$ cần $1$ cốc nước lọc, $10$ g đường và $4$ g hương liệu. Mỗi cốc đồ uống loại $A$ nhận được $6$ điểm thưởng, mỗi cốc đồ uống loại $B$ nhận được $8$ điểm thưởng. Để đạt được số điểm thưởng cao nhất, đội chơi cần pha chế $x$ cốc đồ uống loại $A$ , $y$ cốc đồ uống loại $B$ . Tính $x + y$ .

Trả lời:

Câu 22 (1đ):

Muốn đo chiều cao của một cái cây mà không thể đến được gốc cây, người ta lấy hai điểm $M$ , $N$ trên mặt đất có khoảng cách $MN=5$ m cùng thẳng hàng với gốc cây để đặt hai giác kế. Chân của giác kế có chiều cao $MA=NB=1,2$ m. Lấy điểm $D$ trên thân cây sao cho $A$ , $B$ , $D$ thẳng hàng. Người ta đo được $\widehat{CAD}=\alpha =36^\circ$ và $\widehat{CBD}=\beta =41^\circ$ .

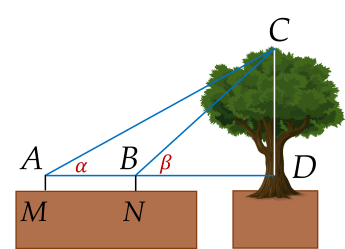
loading...

Tính chiều cao của cây. (Làm tròn kết quả đến hàng phần mười của đơn vị mét)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP