Đề kiểm tra học kì I (đề số 3)

Câu 1 (1đ):

Quy tròn số $223\,254$ đến hàng trăm ta được số

223\,200

.

223\,300

.

223\,000

.

223\,250

.

Câu 2 (1đ):

Câu 3 (1đ):

Câu 4 (1đ):

Giá trị của $E=\sin 36^\circ . \cos 6^\circ - \sin 126^\circ . \cos 84^\circ$ bằng

\dfrac{1}{2}

.

1

.

-1

.

\dfrac{\sqrt{3}}{2}

.

Câu 5 (1đ):

Cho các số thực $a$ , $b$ , $c$ , $d$ và $a<b<c<d$ . Khi đó $\left(a;c \right) \cap \left(b;d \right)=$

\left(a;d \right)

.

\left[b;c \right]

.

\left(b;c \right)

.

\left[ a;d \right]

.

Câu 6 (1đ):

Cho tam giác $ABC$ , gọi $M$ là trung điểm của $BC$ . Mệnh đề nào sau đây sai?

\overrightarrow{CM},\overrightarrow{BC}

cùng phương.

\left| \overrightarrow{CM} \right|=\left| \overrightarrow{BM} \right|

.

\overrightarrow{CM}=\overrightarrow{MB}

.

\overrightarrow{AB}=\overrightarrow{BC}

.

Câu 7 (1đ):

Câu 8 (1đ):

Cho hình vuông $ABCD$ có cạnh $a.$ Khi đó $\overrightarrow{AB}.\overrightarrow{AD}$ bằng

a

.

\dfrac{a^2}{2}

.

0

.

\overrightarrow{AB}.\overrightarrow{AD}=a^2

.

Câu 9 (1đ):

Gọi $A$ là tập nghiệm của phương trình $x^2-3x+2=0$ và tập hợp $B=\Big\{ x \in \mathbb{Z} \, \big| \, 0<x<3 \Big\}$ ; $C=\Big\{ x\in \mathbb{Z}\, \big| \, 1\le x\le 3 \Big\}$ . Khẳng định nào sau đây sai?

B \subset C

.

A \subset C

.

A=C

.

A=B

.

Câu 10 (1đ):

Cho hình thang $ABCD$ có $AB$ song song với $CD$ , $AB=2a$ , $CD=a$ . Gọi $O$ là trung điểm của $AD$ .

Độ dài $\left| \overrightarrow{OB}+\overrightarrow{OC} \right|$ bằng

a

.

3a

.

0

.

\dfrac{3a}2

.

Câu 11 (1đ):

Cho tam giác $ABC$ . Gọi $I$ là trung điểm của $AB$ . Điểm $M$ thỏa mãn hệ thức $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$ là

điểm trên cạnh

IC

sao cho

IM=2MC

.

trung điểm của

IC

.

trung điểm của

BC

.

trung điểm của

IA

.

Câu 12 (1đ):

Cho tam giác $ABC$ và $M$ thỏa mãn $\overrightarrow{BM}=-3\overrightarrow{MC}$ . Mệnh đề nào sau đây đúng?

\overrightarrow{AM}=-\dfrac12\overrightarrow{AB}+\dfrac32\overrightarrow{AC}

\overrightarrow{AM}=\dfrac34\overrightarrow{AB}+\dfrac14\overrightarrow{AC}.

\overrightarrow{AM}=\dfrac14\overrightarrow{AB}+\dfrac34\overrightarrow{AC}.

\overrightarrow{AM}=\dfrac14\overrightarrow{AB}-\dfrac34\overrightarrow{AC}.

Câu 13 (1đ):

Cuối học kì I vừa qua, bạn An đạt được kết quả sáu môn như sau:

Môn	Điểm trung bình
Toán	$7,2$
Văn	$8,0$
Anh	$5,8$
Lý	$7,2$
Hóa	$9,0$
Sinh	$4,6$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Điểm trung bình các môn thi học kì của bạn An là $7,0$ .
b) Điểm trung bình các môn thi học kì của bạn An là $7,3$ .
c) Khoảng biến thiên của bảng điểm của bạn An bằng $3,4$ .
d) Khoảng tứ phân vị bảng điểm của bạn An bằng $2,2$ .

Câu 14 (1đ):

Cho tam giác $ABC$ biết $a=BC=3$ cm, $b=AC=4$ cm, $\widehat{C}=30^\circ$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $c^2=a^2+b^2-2ab\cos C$ .
b) $c \approx 3,05$ cm.
c) $\cos A \approx 0,68$ .
d) $\widehat{A} \approx 77,2^\circ$ .

Câu 15 (1đ):

Một công ty viễn thông tính phí $1$ $000$ đồng mỗi phút gọi nội mạng và $2$ $000$ đồng mỗi phút gọi ngoại mạng. Gọi $x$ và $y$ lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng và Bình muốn số tiền phải trả cho tổng đài luôn thấp hơn $100$ nghìn đồng.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số tiền Bình phải trả cho cuộc gọi nội mạng mỗi tháng là $x$ (nghìn đồng), số tiền phải trả cho cuộc gọi ngoại mạng mỗi tháng là $2y$ (nghìn đồng) và $x \in \mathbb{N}, \, y\in \mathbb{N}$ .
b) $x+2y<100$ .
c) Nếu $50$ và $20$ lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng thì số tiền phải trả cho tổng đài thấp hơn $100$ nghìn đồng.
d) Nếu $50$ và $25$ lần lượt là số phút gọi nội mạng, ngoại mạng trong một tháng thì số tiền phải trả cho tổng đài vượt quá mục tiêu của Bình.

Câu 16 (1đ):

Cho tam giác $ABC$ có trực tâm $H$ và $M$ là trung điểm $BC$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{HA}.\overrightarrow{CB}=1$ .
b) $\overrightarrow{BH}.\overrightarrow{CA}=0$ .
c) $\overrightarrow{MH}.\overrightarrow{MA}=\dfrac{BC^2}{4}$ .
d) $MH^2+MA^2=AH^2+\dfrac{BC^2}{2}$ .

Câu 17 (1đ):

Trên biển Đông, một tàu chuyển động đều từ vị trí $A$ theo hướng N $20^\circ$ W với vận tốc $30$ km/h. Sau $5$ giờ, tàu đến được vị trí $B$ . $A$ cách $B$ bao nhiêu ki lô mét và về hướng S $20^\circ$ E so với $B$ ?

Trả lời:

Câu 18 (1đ):

Câu 19 (1đ):

Muốn đo chiều cao của một cái cây mà không thể đến được gốc cây, người ta lấy hai điểm $M$ , $N$ trên mặt đất có khoảng cách $MN=5$ m cùng thẳng hàng với gốc cây để đặt hai giác kế. Chân của giác kế có chiều cao $MA=NB=1,2$ m. Lấy điểm $D$ trên thân cây sao cho $A$ , $B$ , $D$ thẳng hàng. Người ta đo được $\widehat{CAD}=\alpha =36^\circ$ và $\widehat{CBD}=\beta =41^\circ$ .

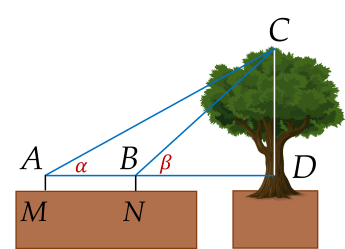
loading...

Tính chiều cao của cây. (Làm tròn kết quả đến hàng phần mười của đơn vị mét)

Trả lời:

Câu 20 (1đ):

Một người thợ mộc làm hai loại sản phẩm là bàn và ghế. Mỗi cái bàn khi bán lãi $150$ nghìn đồng, mỗi cái ghế khi bán lãi $50$ nghìn đồng. Người thợ mộc có thể làm $40$ giờ/tuần và tốn $6$ giờ để làm một cái bàn, $3$ giờ để làm một cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế ít nhất là gấp ba lần số bàn. Một cái bàn chiếm chỗ bằng $4$ cái ghế và ta có phòng để được nhiều nhất $4$ cái bàn. Người thợ mộc phải sản xuất $x$ cái bàn và $y$ cái ghế trong ba tuần để số tiền lãi thu về là lớn nhất. Tính $x + y$ .

Trả lời:

Câu 21 (1đ):

Tam giác $ABC$ vuông cân tại $A$ và nội tiếp trong đường tròn tâm $O$ bán kính $R$ . Gọi $r$ là bán kính đường tròn nội tiếp tam giác $ABC$ . Khi đó tỉ số $\dfrac{R}{r}$ có dạng $a+b\sqrt{c}$ , với $a, \, b, \, c \in \mathbb{N}$ và $c$ là số nguyên tố. Tính giá trị của biểu thức $T=a+b+c$ .

Trả lời:

Câu 22 (1đ):

Bạn Khương bản Mộc thống kê số ngày có mưa, có sương mù ở bản mình trong tháng 3 vào một thời điểm nhất định và được kết quả như sau: $14$ ngày có mưa, $15$ ngày có sương mù, trong đó $10$ ngày có cả mưa và sương mù. Trong tháng 3 đó có bao nhiêu ngày không có mưa và không có sương mù?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP