Đề kiểm tra học kì I (đề số 2)

Câu 1 (1đ):

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{u}=(1 ; 1 ; 0)$ và $\overrightarrow{v}=(2 ; 0 ;-1)$ . Độ dài $|\overrightarrow{u}+2 \overrightarrow{v}|$ bằng

\sqrt{30}

.

2 \sqrt{2}

.

2 .

\sqrt{22}

.

Câu 2 (1đ):

Trong không gian với hệ tọa độ $O x y z$ , cho hai điểm $A(1 ; 2 ;-3)$ và $B(-3 ; 4 ; 5)$ . Tọa độ trung điểm $I$ của đoạn thẳng $A B$ là

I(-1 ; 3 ; 1).

I(2 ;-1 ;-4).

I(-1 ;-3 ; 1).

I(-2 ; 1 ; 4).

Câu 3 (1đ):

Một sinh viên đo độ dài của một số lá dương xỉ trưởng thành, kết quả như sau:

Lớp độ dài (cm)	Tần số
$\big[10 \, ; \, 20\big)$	$8$
$\big[20 \, ; \, 30\big)$	$6$
$\big[30 \, ; \, 40\big)$	$24$
$\big[40 \, ; \, 50\big)$	$10$

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

35

.

45

.

40

.

30

.

Câu 4 (1đ):

Giá trị lớn nhất của hàm số $y=-x^4+4x^2$ trên đoạn $\left[ -1;2 \right]$ bằng

5

.

4

.

1

.

3

.

Câu 5 (1đ):

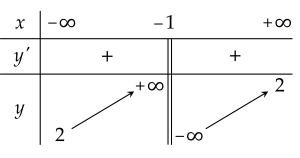
loading...

Hình trên là bảng biến thiên của hàm số nào trong bốn hàm số dưới đây?

y=\dfrac{2x+3}{x+1}

.

y=\dfrac{x-1}{x+1}

.

y=\dfrac{2x-1}{x+1}

.

y=\dfrac{2x-1}{x-1}

.

Câu 6 (1đ):

Phương trình tiếp tuyến của đồ thị hàm số $y=x^3-3x^2+1$ tại điểm $A(3;1 )$ là

y=-9x-26.

y=9x-3.

y=-9x-3.

y=9x-26.

Câu 7 (1đ):

Hình vẽ sau mô tả một sân tennis với kích thước theo tiêu chuẩn quốc tế (kích thước được làm tròn đến hàng phần mười của đơn vị mét). Chọn hệ trục $Oxyz$ cho sân đó (đơn vị trên mỗi trục là mét) cùng hai điểm $A,\,B$ .

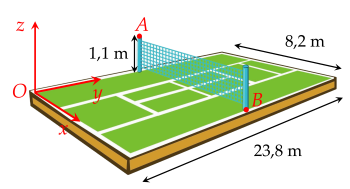
loading...

Tọa độ $\overrightarrow{AB}$ là

(0\ ;\ 8,2\ ;\ -1,1)

.

(8,2\ ;\ 0\ ;\ 1,1)

.

(8,2\ ;\ 0\ ;\ -1,1)

.

(0\ ;\ 8,2\ ;\ 1,1)

.

Câu 8 (1đ):

Cho tứ diện $A B C D$ có $G$ là trọng tâm tam giác $B C D$ . Đặt $\overrightarrow{x}=\overrightarrow{A B} ; \, \overrightarrow{y}=\overrightarrow{A C} ; \, \overrightarrow{z}=\overrightarrow{A D}$ . Biểu diễn $\overrightarrow{A G}$ theo $\overrightarrow{x};\overrightarrow{y};\overrightarrow{z}$ ta được

\overrightarrow{A G}=-\dfrac{2}{3}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})

.

\overrightarrow{A G}=-\dfrac{1}{3}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})

.

\overrightarrow{A G}=\dfrac{1}{3}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})

.

\overrightarrow{A G}=\dfrac{2}{3}(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z})

.

Câu 9 (1đ):

Hàm số nào sau đây đồng biến trên khoảng $\big(-\infty ; + \infty\big)$ ?

y=\dfrac{-x^2}{x+1}

.

y=x^3+x

.

y=x^3-x

.

y=\dfrac{x-1}{x+2}

.

Câu 10 (1đ):

Cho hàm số $y=f(x)$ xác định trên $\mathbb{R} \backslash \{x_2\}$ và có bảng xét dấu của đạo hàm như sau:

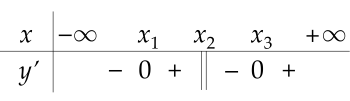
loading...

Số điểm cực trị của hàm số $y=f(x)$ là

2

.

4

.

1

.

3

.

Câu 11 (1đ):

Đồ thị hàm số $y=\sqrt{x^2+2x+2}$ có bao nhiêu đường tiệm cận xiên?

1

.

0

.

3

.

2

.

Câu 12 (1đ):

Một tác giả muốn xuất bản một cuốn sách Toán học. Biết phí xuất bản là $7$ triệu đồng và giá tiền in mỗi cuốn sách là $50$ nghìn đồng. Gọi $t \ge 1$ là số cuốn sách sẽ in và $f(t)$ (nghìn đồng) là chi phí trung bình của mỗi cuốn sách. Phương trình đường tiệm cận ngang của đồ thị hàm số $y = f(t)$ là

y = 50

.

y = 30

.

y = 45

.

y = 60

.

Câu 13 (1đ):

Cho hình lập phương $ABCD. A'B'C'D'$ có cạnh bằng $a$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{A B}+\overrightarrow{B' C'}+\overrightarrow{C D}+\overrightarrow{D' A'}=\overrightarrow{0}$ .
b) $\overrightarrow{A B'} . \overrightarrow{C D'}=0$ .
c) $\left\|\overrightarrow{A C'}\right\| = \sqrt{3}$ .
d) $\overrightarrow{A D'} . \overrightarrow{A B'}=a^{2}\sqrt{3}$ .

Câu 14 (1đ):

Bảng số liệu ghép nhóm dưới đây cho biết dân số theo độ tuổi của người dân ở trong một nhóm người lao động.

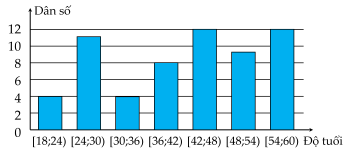
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số người lao động tham gia thống kê về độ tuổi là $59$ người.
b) Độ tuổi trung bình của nhóm người lao động trên là $41,8$ .
c) Độ tuổi trung vị của nhóm người lao động trên là $43,5$ .
d) Phương sai của mẫu số liệu ghép nhóm trên là $135,86$

Câu 15 (1đ):

Một khúc gỗ có dạng hình khối nón có bán kính đáy $r=2$ m, chiều cao $l=6$ m. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ.

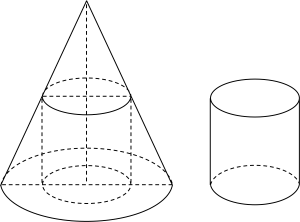
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Đặt $x$ là bán kính đáy hình trụ, $h$ là chiều cao của hình trụ. Khi đó chiều cao của khối trụ tính theo bán kính đáy hình trụ là $h=-3 x+6$ (m) với $0\lt x\lt 2$ .
b) Hàm số xác định thể tích của khối trụ trên là $V=6 x^{2}-3 x^{3}$ (m $^3$ ), $\forall x \in(0 ; 2)$ .
c) Giả sử bác thợ mộc chế tác khúc gỗ đó thành hình trụ có bán kính đáy bằng chiều cao, khi đó thể tích của khối trụ là $V=\dfrac{27}{8} \pi$ (m $^3$ ).
d) Thể tích lớn nhất của khối gỗ mà bác thợ mộc chế tác là $V_{\max }=\dfrac{32 \pi}{9}$ (m $^3$ ).

Câu 16 (1đ):

Một vật chuyển động có phương trình quãng đường tính bằng mét phụ thuộc thời gian $t$ tính bằng giây được biểu thị bởi hàm số $f(t)=-t^{3}+9 t^{2}+21 t$ (m).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Quãng đường mà vật đi được sau $2$ s kể từ lúc bắt đầu chuyển động là $70$ m .
b) Vận tốc lớn nhất của vật thể là $21$ (m/s).
c) Vận tốc của vật tăng từ lúc bắt đầu chuyển động đến giây thứ $3.$
d) Kể từ lúc bắt đầu chuyển động đến khi dừng hẳn, vật đi được quãng đường là $250$ m.

Câu 17 (1đ):

An tìm hiểu hàm lượng chất béo (đơn vị: g) có trong $100$ g mỗi loại thực phẩm. Sau khi thu thập dữ liệu về $60$ loại thực phẩm, An lập được bảng thống kê.

Hàm lượng chất béo (g)	Tần số
$[2;6)$	$2$
$[6;10)$	$6$
$[10;14)$	$10$
$[14;18)$	$13$
$[18;22)$	$16$
$[22;26)$	$13$

Tính khoảng tứ phân vị của mẫu số liệu trên. (Làm tròn đến chữ số thập phân thứ nhất)

Trả lời: .

Câu 18 (1đ):

Nếu một vật có khối lượng $m$ (kg) thì lực hấp dẫn $\overrightarrow{P}$ (N) của Trái Đất tác dụng lên vật được xác định theo công thức: $\overrightarrow{P}=m . \overrightarrow{g}$ , trong đó $\overrightarrow{g}$ là gia tốc rơi tự do có độ lớn $g=9,8$ m/s $^2$ . Một con khỉ có cân nặng $5$ kg đang biểu diễn xiếc. Nó nắm tay vào dây để treo mình đứng yên như hình vẽ.

loading...

Khi dây ở vị trí cân bằng, tính độ lớn của lực căng dây $\overrightarrow{T_1}$ , đơn vị N (làm tròn kết quả đến chữ số thập phân thứ nhất)

Trả lời:

Câu 19 (1đ):

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc $\left[-1; 6\right]$ để hàm số $y=\dfrac{1}{3} \left(m^{2} -1\right)x^{3} +\left(m+1\right)x^{2} +3x-1$ đồng biến trên $(-\infty ; +\infty)$ ?

Trả lời:

Câu 20 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ:

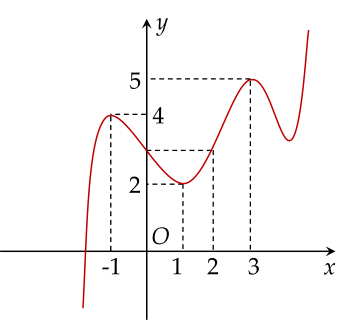
loading...

Gọi $M, m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=f(|x-2|)$ trên đoạn $[-1 ; 5]$ . Tính giá trị của $M+m$ .

Trả lời:

Câu 21 (1đ):

Một hợp tác xã nuôi cá thí nghiệm trong hồ. Người ta thấy rằng nếu trên mỗi đơn vị diện tích của mặt hồ có $n$ con cá thì trung bình mỗi con cá sau một vụ cân nặng $P(n) = 480 – 20n$ (gam). Cần phải thả số lượng cá trên một đơn vị diện tích của mặt hồ là bao nhiêu con để cân nặng trung bình của số cá đó lớn nhất?

Trả lời:

Câu 22 (1đ):

Tại một công ty sản xuất đồ chơi an toàn cho trẻ em, công ty phải chi $40\,000$ USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi $A$ , công ty phải trả $6$ USD cho nguyên liệu ban đầu và nhân công. Gọi $x$ , ( $x \ge 1$ ) là số đồ chơi $A$ mà công ty đã sản xuất và $P(x)$ (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất $x$ đồ chơi $A$ . Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi $A$ là $F(x)=\dfrac{P(x)}{x}$ . Xem $y = F(x)$ là hàm số theo $x$ xác định trên nửa khoảng $\left[ 1;+\infty \right)$ có phương trình đường tiệm cận ngang là $y = b$ . Tính $b$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP