Đề kiểm tra học kì I (đề số 1) chân trời sáng tạo

Câu 1 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên sau:

loading...

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

(-\infty ;\,-2)

.

(-1;\,1)

.

(4;\,+\infty)

.

(0;\,1)

.

Câu 2 (1đ):

Khẳng định nào sau đây đúng về hàm số $y=f(x)=\dfrac14x^4-2x^2+1$ ?

Hàm số có một điểm cực đại và không có điểm cực tiểu.

Hàm số có một điểm cực tiểu và hai điểm cực đại.

Hàm số có một điểm cực đại và hai điểm cực tiểu.

Hàm số có một điểm cực tiểu và một điểm cực đại.

Câu 3 (1đ):

Cho hàm số $y=f\left( x \right)$ có bảng xét dấu đạo hàm như sau.

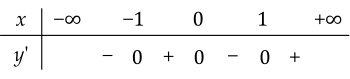
loading...

Mệnh đề nào sau đây đúng?

\underset{\left( -1;\,+\infty \right)}{\mathop{\min }}\,f\left( x \right)=f\left( 0 \right)

.

\underset{\left( 0;\,+\infty \right)}{\mathop{\max}}\,f\left( x \right)=f\left( 1 \right)

.

\underset{\left( -\infty ;\,-1 \right)}{\mathop{\min }}\,f\left( x \right)=f\left( -1 \right)

.

\underset{\left( -1;\,1 \right]}{\mathop{\max}}\,f\left( x \right)=f\left( 0 \right)

.

Câu 4 (1đ):

Hệ số góc của tiếp tuyến với đồ thị hàm số $y=x^3+x$ tại điểm $M(-1\,;\,0 )$ là

1

.

-2

.

4

.

0

.

Câu 5 (1đ):

Trong không gian

Oxyz

, cho hai điểm

A(2;1;3)

,

B(1;-1;5)

. Độ dài đoạn thẳng

AB

là

5

.

3

.

4

.

6

.

Câu 6 (1đ):

Cho hình chóp

S.ABCD

có đáy

ABCD

là hình bình hành tâm

O

. Khẳng định nào sau đây đúng?

\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\dfrac{1}{4}\overrightarrow{SO}

.

\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\dfrac{1}{2}\overrightarrow{SO}

.

\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=2\overrightarrow{SO}

.

\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=4\overrightarrow{SO}

.

Câu 7 (1đ):

Bảng sau cho biết kết quả điều tra về chiều cao của học sinh khối lớp $10$ .

Chiều cao (cm)	Số học sinh
$[150;152)$	$5$
$[152;154)$	$18$
$[154;156)$	$40$
$[156;158)$	$26$
$[158;160)$	$8$
$[160;162)$	$3$

Khoảng biến thiên của mẫu số liệu trên là

10

.

16

.

15

.

12

.

Câu 8 (1đ):

Giá trị nhỏ nhất của hàm số $y={{x}^{3}}+\dfrac{3}{x}$ trên khoảng $\left( 0;+\infty \right)$ là

4

.

4\sqrt[4]{3}

.

2

.

2\sqrt{3}

.

Câu 9 (1đ):

Tiệm cận xiên của đồ thị hàm số $y=\dfrac{{{x}^{2}}+3x+5}{x+2}$ là

y=x+3.

y=x.

y=x+2.

y=x+1.

Câu 10 (1đ):

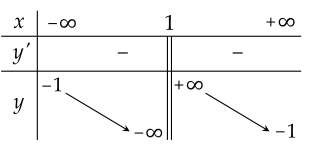
loading...

Hàm số nào dưới đây có bảng biến thiên như hình vẽ trên?

y=\dfrac{x-2}{x-1}.

y=\dfrac{-x-2}{x-1}.

y=\dfrac{x+3}{x-1}.

y=\dfrac{-x+3}{x-1}.

Câu 11 (1đ):

Theo định luật II Newton: Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật: $\overrightarrow{F}=m\overrightarrow{a}$ trong đó $\overrightarrow{a}$ là vectơ gia tốc, đơn vị m/s $^2$ ; $\overrightarrow{F}$ là vectơ lực tác dụng lên vật; $m$ kg là khối lượng của vật.

loading...

Muốn truyền cho quả bóng có khối lượng $0,5$ kg một gia tốc $50$ m/s $^2$ thì cần một lực đá có độ lớn là bao nhiêu?

40

N.

35

N.

25

N.

30

N.

Câu 12 (1đ):

Mỗi ngày bác Tâm đều đi bộ để rèn luyện sức khoẻ. Quãng đường đi bộ mỗi ngày của bác Tâm trong $20$ ngày được thống kê lại trong bảng sau:

Quãng đường (km)	Số ngày
$[2,7;3)$	$3$
$[3;3,3)$	$6$
$[3,3;3,6)$	$5$
$[3,6;3,9)$	$4$
$[3,9;4,2)$	$2$

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là

0,9.

0,975.

0,5.

0,575.

Câu 13 (1đ):

Một bể chứa $5\,000$ lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ $30$ gam muối cho mỗi lít nước với tốc độ $25$ lít/phút.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Sau $10$ phút bơm số lượng muối trong bể là $300$ gam.
b) Nếu bơm trong một giờ đồng hồ thì số lượng muối trong bể không vượt quá $2$ kg.
c) Nồng độ muối trong bể sau $t$ phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là $f(t )=\dfrac{30t}{200+t}$ .
d) Khi $t$ đủ lớn thì nồng độ muối trong bể sẽ tiến gần đến mức $30$ (gam/lít).

Câu 14 (1đ):

Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:

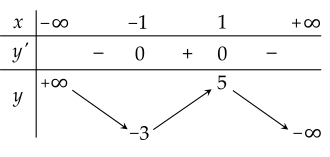
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Phương trình $2f(x)=5$ có $3$ nghiệm.
b) Hàm số đồng biến trên khoảng $(-3 ; 5)$ .
c) Giá trị lớn nhất của hàm số trên $[-1 ; 2]$ bằng $1$ .
d) Hàm số đã cho có $2$ cực trị.

Câu 15 (1đ):

Cho tứ diện $ABCD$ có $AB\,=\,AC=AD=BC=BD=a$ , $\Delta BCD$ vuông cân tại $B$ . Gọi $M$ , $N$ lần lượt là trung điểm các cạnh $AB$ , $CD$ .

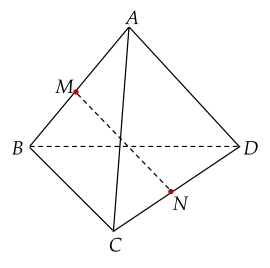
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AC}+\overrightarrow{DB}$ .
b) $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}$ .
c) $\overrightarrow{AB}.\overrightarrow{BC}=\dfrac{1}{2}{a^2}$ .
d) $(\overrightarrow{AD},\overrightarrow{BC})=120^\circ$ .

Câu 16 (1đ):

Bảng sau thống kê thời gian (đơn vị: phút) tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn Bình và bạn An.

Thời gian (phút)	Số ngày tập của Bình	Số ngày tập của An
$[15;20)$	$5$	$5$
$[20;25)$	$10$	$5$
$[25;30)$	$10$	$15$
$[30;35)$	$2$	$3$
$[35;40)$	$1$	$0$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Khoảng biến thiên của mẫu số liệu về thời gian tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn An là $20$ .
b) Khoảng tứ phân vị của mẫu số liệu về thời gian tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn Bình là $28$ .
c) Khoảng tứ phân vị của mẫu số liệu về thời gian tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn An là $22$ .
d) Dựa vào khoảng tứ phân vị của hai mẫu số liệu trên thì thời gian tập thể dục buổi sáng mỗi ngày trong tháng 2 năm 2023 của bạn Bình phân tán hơn bạn An.

Câu 17 (1đ):

Trong bài thực hành của môn huấn luyện quân sự có tình huống chiến sĩ phải bơi qua một con sông để tấn công một mục tiêu ở phía bờ bên kia sông. Biết rằng lòng sông rộng $100$ m và vận tốc bơi của chiến sĩ bằng một nửa vận tốc chạy trên bờ. Nếu như dòng sông là thẳng, mục tiêu ở cách chiến sĩ $1$ km theo đường chim bay thì người chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? (kết quả làm tròn đến hàng đơn vị)

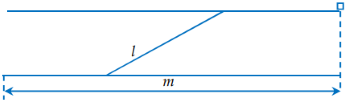
loading...

Trả lời:

Câu 18 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ:

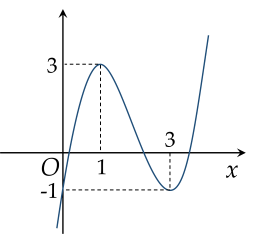
loading...

Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(| x+m | )=m$ có đúng $6$ nghiệm phân biệt?

Trả lời:

Câu 19 (1đ):

Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức $G(x)=0,024x^2(30-x)$ , trong đó $x$ là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp ( $x$ được tính bằng mg). Tìm lượng thuốc $x$ tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.

Trả lời:

Câu 20 (1đ):

Cho hình hộp $A B C D . A' B' C' D'$ . Một đường thẳng $\Delta$ cắt các đường thẳng $A A', \, B C, \, C' D'$ lần lượt tại $M, \, N, \, P$ sao cho $\overrightarrow{N M}=2 \overrightarrow{N P}$ . Tính $\dfrac{M A}{M A'}$ .

Trả lời:

Câu 21 (1đ):

Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật $ABCD$ , mặt phẳng $(ABCD )$ song song với mặt phẳng nằm ngang. Khung sắt đó được đặt vào móc $E$ của chiếc cần cẩu sao cho các đoạn dây cáp $EA;\,EB;\,EC;\,ED$ bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc $\alpha$ .

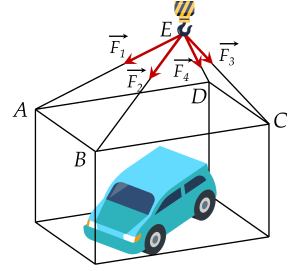
loading...

Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết các lực căng $\overrightarrow{F_1};\,\overrightarrow{F_2};\,\overrightarrow{F_3};\,\overrightarrow{F_4}$ đều có cường độ là $4\,800\,\text{N}$ , trọng lượng của cả khung sắt chứa xe ô tô là $7\,200\sqrt{6}\,\text{N}$ . Tính $\sin \alpha$ . (làm tròn kết quả đến chữ số hàng phần trăm).

Trả lời:

Câu 22 (1đ):

Cho bảng mẫu số liệu ghép nhóm sau:

Nhóm	Tần số
$[20;26)$	$7$
$[26;32)$	$9$
$[32;38)$	$5$
$[38;44)$	$4$
$[44;50)$	$11$

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến chữ số hàng phần trăm)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP