Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 1) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Góc có số đo 52π đổi sang độ là
Cho cấp số cộng (un). Biết un=−5n+10∀n∈N∗. Công sai d của cấp số cộng (un) là
Cho dãy số (un) với un=sinnπ. Khi đó, dãy số (un)
Nghiệm của phương trình cot(x+2)=1 là
Xét hàm số y=sinx trên đoạn [−π;0]. Khẳng định nào sau đây đúng?
Giá trị lớn nhất của hàm số y=3sinx là
Số đo của góc 12π khi đổi sang độ là
Tổng n số hạng đầu tiên của một cấp số cộng cho bởi Sn=3n2−n. Công sai của cấp số cộng đó là
Tổng các nghiệm của phương trình tan(2x−15∘)=1 trên khoảng (−90∘;90∘) bằng
Cho cấp số cộng (un) có u5=−15, u20=60. Tổng của 10 số hạng đầu tiên của cấp số cộng này là
Cho hai đồ thị hàm số y=sin(x+4π) và y=sinx.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: sin(x+4π)=sinx. |
|
| b) Hoành độ giao điểm của hai đồ thị là x=83π+kπ,(k∈Z). |
|
| c) Khi x∈[0;2π] thì hai đồ thị hàm số cắt nhau tại ba điểm. |
|
| d) Khi x∈[0;2π] thì toạ độ giao điểm của hai đồ thị hàm số là: (85π;sin85π); (87π;sin87π). |
|
Cho cấp số nhân (un) có công bội nguyên và các số hạng thoả mãn {u4−u2=54u5−u3=108
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Số hạng đầu của cấp số nhân bằng 9. |
|
| b) Công bội của cấp số nhân q=3. |
|
| c) Tổng của 9 số hạng đầu tiên bằng 4599. |
|
| d) Số 576 là số hạng thứ 6 của cấp số nhân. |
|
Cho các hàm số f(x)=3−2sinx và g(x)=tan2x−31cosx.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số f(x) có tập xác định D=R. |
|
| b) Hàm số f(x) là hàm số tuần hoàn. |
|
| c) Hàm số g(x) xác định khi x=k2π,(k∈Z). |
|
| d) Hàm số g(x) là hàm số không tuần hoàn. |
|
Cho phương trình lượng giác sin(3x+3π)=−23.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Phương trình có nghiệm x=−9π+k32πx=3π+k32π,(k∈Z). |
|
| b) Phương trình có nghiệm âm lớn nhất bằng −92π. |
|
| c) Trên khoảng (0;2π) phương trình đã cho có 3 nghiệm. |
|
| d) Tổng các nghiệm của phương trình trong khoảng (0;2π) bằng 97π. |
|
Nguời ta thiết kế một cái tháp gồm 10 tầng theo cách: Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt của tầng 1 bằng nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là 12288 m2, tính diện tích bề mặt trên cùng của tháp (đơn vị mét vuông).
Trả lời:
Cô Lan đang tiết kiệm để mua laptop. Trong tuần đầu tiên, cô ấy để dành 200 đô la, và trong mỗi tuần tiếp theo, cô đã thêm 16 đô la vào tài khoản tiết kiệm của mình. Chiếc laptop cô Lan cần mua có giá 1000 đô la. Vào tuần thứ bao nhiêu thì cô ấy có đủ tiền để mua chiếc laptop đó?
Trả lời:
Số giờ có ánh sáng của một thành phố A trong ngày thứ t của năm 2025 được cho bởi một hàm số y=4sin178π(t−60)+10, với t∈Z và 60<t≤365. Vào ngày thứ bao nhiêu trong năm đó thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?
Trả lời:
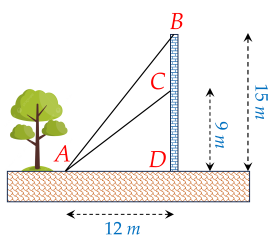
Từ một vị trí A, người ta buộc hai sợi cáp AB và AC đến một cái trụ cao 15 m, được dựng vuông góc với mặt đất, chân trụ ở vị trí D. Biết CD=9 m và AD=12 m. Tìm góc nhọn α=BAC tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng α (làm tròn đến hàng phần mười, đơn vị độ).
Trả lời:
Gọi n là số nghiệm của phương trình sin(2x+30∘)=23 trên khoảng (−180∘;180∘). Tìm n.
Trả lời:
Sinh nhật bạn của An vào ngày 1 tháng năm. An muốn mua một món quà sinh nhật cho bạn thân của mình nên quyết định bỏ ống heo 1000 đồng vào ngày 01 tháng 01 năm 2016, sau đó cứ liên tục ngày sau hơn ngày trước 1000 đồng. Đến ngay trước ngày sinh nhật của bạn thân, An đã tích lũy được bao nhiêu tiền? (ghi kết quả dưới dạng số thập phân, đơn vị nghìn đồng)
Trả lời:
