Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Dấu hiệu nhận biết hình bình hành SVIP
Đây là bản xem thử, hãy nhấn Luyện tập ngay để bắt đầu luyện tập với OLM
Câu 1 (1đ):
Điền vào dấu ... để hoàn thành khẳng định: "Tứ giác có ... là hình chữ nhật."
bốn cạnh bằng nhau.
hai góc vuông.
bốn góc vuông.
các cạnh đối song song.
Câu 2 (1đ):
Hình bình hành cần có thêm điều kiện nào sau đây thì trở thành hình chữ nhật?
Có hai đường chéo vuông góc.
Có hai cạnh kề bằng nhau.
Có một góc vuông.
Có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Câu 3 (1đ):
Hình bình hành ABCD là hình chữ nhật khi
AC // BD.
AC=BD.
AC=2.BD.
AC⊥BD.
Câu 4 (1đ):
Chọn khẳng định sai.
Hình bình hành có một góc vuông là hình chữ nhật.
Hình thang cân có một góc vuông là hình chữ nhật.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Hình thang có một góc vuông là hình chữ nhật.
Câu 5 (1đ):
Chọn khẳng định đúng.
Hình bình hành ABCD là hình chữ nhật khi
AC=BD.
AC⊥BD.
AB=BC.
BC=CD.
Câu 6 (1đ):
Chọn khẳng định đúng.
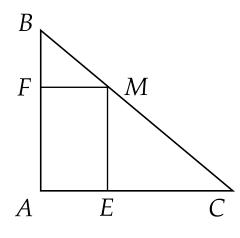
Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
ΔABC vuông tại A.
ΔABC đều.
ΔABC vuông tại C.
ΔABC vuông tại B.
Câu 7 (1đ):
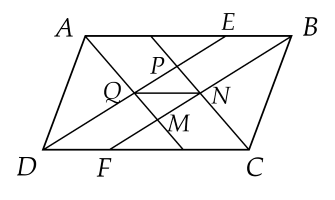
Cho hình bình hành ABCD có AB=a, BC=b, (a>b). Các phân giác trong của các góc A,B,C,D tạo thành tứ giác MNPQ. Tứ giác MNPQ là hình gì?
Hình chữ nhật.
Hình bình hành.
Hình thang cân.
Hình thang vuông.
Câu 8 (1đ):
Khẳng định nào sau đây sai?
Hình thang cân có một góc vuông là hình chữ nhật.
Tứ giác có bốn góc bằng nhau là hình chữ nhật.
Hình bình hành có hai đường chéo vuông góc với nhau là hình chữ nhật.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
25%
Đúng rồi !

Hôm nay, bạn còn lượt làm bài tập miễn phí.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
OLMc◯2022

Bạn có thể đánh giá bài học này ở đây