Dao động điều hòa SVIP

I. Dao động

1. Thí nghiệm

Treo một quả cầu nhỏ, nặng vào một sợi dây nhẹ không dãn ta có con lắc đơn. Kéo vật lệch khỏi vị trí cân bằng một đoạn nhỏ rồi thả ra cho vật chuyển động. Khi đó vật sẽ chuyển động qua lại quanh vị trí cân bằng.

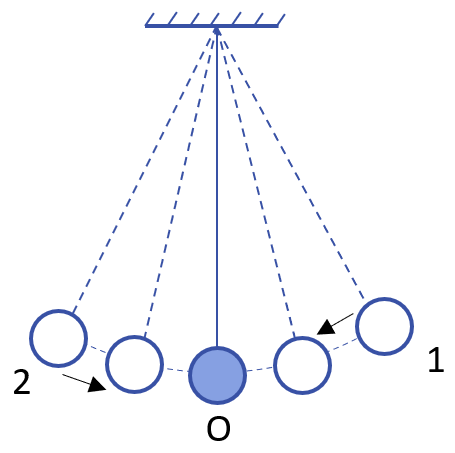
 Hình 1. Sơ đồ biểu diễn chuyển động của quả cầu nhỏ

Chuyển động qua lại quanh một vị trí cân bằng được gọi là dao động.

2. Dao động tự do

Ở Hình 1, khi đi từ vị trí 1 qua vị trí cân bằng O đến vị trí 2 rồi quay ngược lại, đi qua O trở về vị trí cũ 1 thì quả cầu đã thực hiện được một dao động. Nếu không có lực cản thì chuyển động của quả cầu cứ thế tự tiếp diễn, dao động của quả cầu là dao động tự do.

Trong thực tế, lực cản làm cho năng lượng dao động của vật bị giảm dần và năng lượng này cuối cùng chuyển hóa thành năng lượng nhiệt. Các dao động sẽ bị tắt dần.

3. Biên độ, chu kì, tần số của dao động

Độ dịch chuyển lớn nhất của vật dao động so với vị trí cân bằng được gọi là biên độ của dao động, kí hiệu là $A$. Biên độ của dao động là một số dương.

Khoảng thời gian để vật thực hiện một dao động được gọi là chu kì của dao động, kí hiệu là $T$. Đơn vị của chu kì là giây.

Số dao động vật thực hiện được trong một giây được gọi là tần số của dao động, kí hiệu là $f$. Đơn vị của tần số là hertz (kí hiệu là Hz). 1 Hz là một dao động trong một giây.

II. Dao động điều hòa

1. Định nghĩa

Treo một vật nhỏ, nặng vào đầu tự do của một lò xo nhẹ ta có con lắc lò xo. Kéo vật lệch khỏi vị trí cân bằng rồi thả ra cho chuyển động.

Dao động của con lắc lò xo theo trục $x$ thẳng đứng tại các thời điểm khác nhau được biểu diễn như hình dưới. Gọi \(t=0\) là thời điểm bắt đầu quan sát, \(x=0\) là vị trí cân bằng của quả cầu.

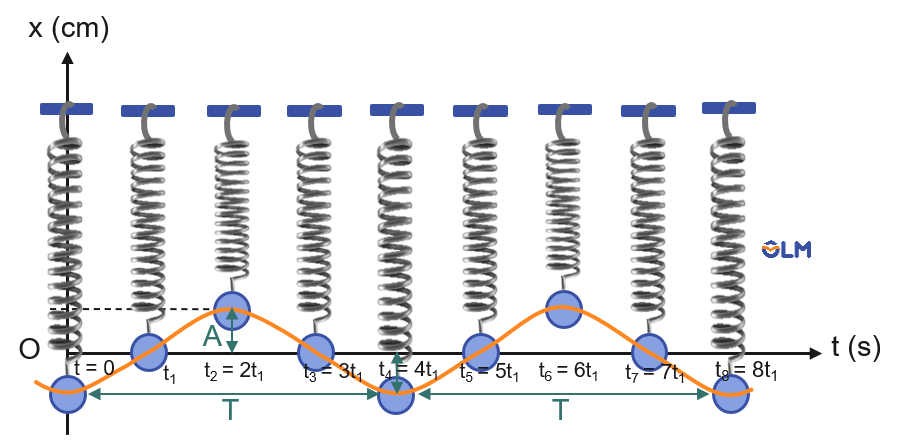
Hình 2. Dao động của con lắc lò xo

Đường cong trên hình là đồ thị dao động của con lắc. Nó cho biết vị trí của quả cầu trên trục $x$ tại những thời điểm khác nhau. Đường cong này có dạng hình sin.

Phương trình của dao động điều hòa (tương ứng với đồ thị trên):

\(x=A\cos\left(\omega t+\varphi\right)\)

Trong đó, \(A\), \(\omega\) và \(\varphi\) là các hằng số.

• \(x\) là li độ dao động.
• \(A\) là biên độ dao động.
• \(\left(\omega t+\varphi\right)\) là pha của dao động ở thời điểm \(t\).
• \(\varphi\) là pha ban đầu của dao động.

Dao động được mô tả bằng phương trình \(x=A\cos\left(\omega t+\varphi\right)\) gọi là dao động điều hòa.

Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.

2. Tần số góc

Đại lượng \(\omega\) được gọi là tần số góc. Đơn vị: radian trên giây (rad/s).

Ta có: \(\omega=\dfrac{2\pi}{T}=2\pi f\)

3. Vận tốc và gia tốc trong dao động điều hòa

Phương trình của vận tốc và gia tốc của một vật dao động điều hòa có li độ là \(x=A\cos\left(\omega t+\varphi\right)\):

\(\text{v}=-\omega A\sin\left(\omega t+\varphi\right)\)

\(a=-\omega^2A\cos\left(\omega t+\varphi\right)\)

• Vận tốc và gia tốc của vật dao động điều hòa cũng biến thiên tuần hoàn theo quy luật hàm số sin (cosin) cùng chu kì $T$ của li độ
• Mối liên hệ giữa gia tốc và li độ của vật dao động điều hòa là: \(a=-\omega^2x\)

4. Pha của dao động và độ lệch pha

Pha của dao động tại một thời điểm được tính bằng số phần đã thực hiện của một chu kì, kể từ khi bắt đầu chu kì đó.

Trong phương trình của dao động điều hòa: \(x=A\cos\left(\omega t+\varphi\right)\), đại lượng \(\left(\omega t+\varphi\right)\) là pha của dao động điều hòa tại thời điểm $t$.

Tại thời điểm $t=0$, pha của dao động là \(\varphi\), do đó \(\varphi\) được gọi là pha ban đầu của dao động.

Độ lệch pha giữa hai dao động cùng chu kì

Độ lệch pha là đại lượng không đổi, không phụ thuộc vào thời điểm quan sát.

• Nếu \(\varphi_1>\varphi_2\) thì dao động 1 sớm pha hơn dao động 2.
• Nếu \(\varphi_1< \varphi_2\) thì dao động 1 trễ pha hơn dao động 2.
• Nếu \(\varphi_1=\varphi_2\) thì dao động 1 cùng (đồng) pha với dao động 2.
• Nếu \(\varphi_1=\varphi_2\pm\pi\) thì dao động 1 ngược pha với dao động 2.

1. Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin (hay sin) của thời gian.

2. Phương trình của dao động điều hòa là \(x=A\cos\left(\omega t+\varphi\right)\), trong đó \(x\) là li độ; \(A\) là biên độ; \(\varphi\) là pha ban đầu.

3. Chu kì \(T\) là khoảng thời gian để vật thực hiện một dao động. Đơn vị của chu kì là giây (s).

4. Tần số \(f\) là số dao động mà vật thực hiện được trong một giây. Đơn vị của tuần số là một trên giây (1/s), gọi là héc (kí hiệu là Hz).

5. Trong dao động điều hòa, giữa tần số góc \(\omega\), chu kì \(T\) và tần số \(f\) có mối liên hệ:

\(\omega=\dfrac{2\pi}{T}=2\pi f\)

Đơn vị của tần số góc là rađian trên giây (rad/s).

6. Độ lệch pha giữa hai dao động điều hòa cùng chu kì luôn bằng độ lệch pha ban đầu.

7. Phương trình của vận tốc và gia tốc của một vật dao động điều hòa có li độ là \(x=A\cos\left(\omega t+\varphi\right)\):

\(\text{v}=-\omega A\sin\left(\omega t+\varphi\right)\)

\(a=-\omega^2A\cos\left(\omega t+\varphi\right)\)

8. Đồ thị của vận tốc, gia tốc theo thời gian là đường hình sin. Vận tốc của vật dao động sớm pha \(\dfrac{\pi}{2}\) so với li độ, còn gia tốc của vật dao động ngược pha so với li độ.