Công thức nhân xác suất cho hai biến cố độc lập SVIP

1. CÔNG THỨC NHÂN XÁC SUẤT CHO HAI BIẾN CỐ ĐỘC LẬP

a. Công thức

Nếu hai biến cố $A$ và $B$ độc lập với nhau thì $P(A B)=P(A) . P(B).$ Công thức này gọi là công thức nhân xác suất cho hai biến cố độc lập.

b. Chú ý

Với hai biến cố $A$ và $B$, nếu $P(A B) \neq P(A) P(B)$ thì $A$ và $B$ không độc lập.

Ví dụ 1. Biết rằng xác suất giành huy chương của vận động viên An và vận động viên Bình tương ứng là $0,8$ và $0,94$. Gọi $A$ là biến cố "Vận động viên An đạt huy chương"; $B$ là biến cố "Vận động viên Bình đạt huy chương".

a) Giải thích tại sao hai biến cố $A$ và $B$ là độc lập.

b) Tính xác suất để cả hai vận động viên đạt huy chương.

c) Sử dụng sơ đồ hình cây, tính xác suất để:

- Cả hai vận động viên không đạt huy chương;

- Vận động viên An đạt huy chương, vận động viên Bình không đạt huy chương;

- Vận động viên An không đạt huy chương, vận động viên Bình đạt huy chương. 

Lời giải

a) Vì hai vận động viên An và Bình thi đấu hai môn thể thao khác nhau nên hai biến cố $A$ và $B$ là độc lập.

b) Vì $A$ và $B$ là hai biến cố độc lập nên áp dụng công thức nhân xác suất, ta có:

$P(A B)=P(A) P(B)=0,8 . 0,9=0,72.$

c) Ta dùng sơ đồ hình cây để mô tả như sau:

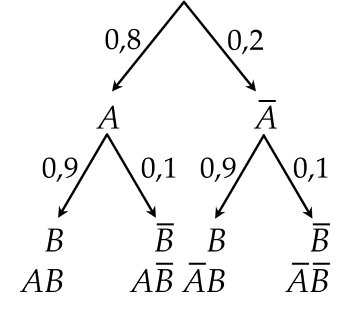
Theo sơ đồ hình cây, ta có: $P(\overline{A} \overline{B})=0,2 . 0,1=0,02$

$P(A \overline{B})=0,8 . 0,1=0,08 $

$P(\overline{A} B)=0,2 . 0,9=0,18$.

2. VẬN DỤNG

Ví dụ 2. Số liệu thống kê tại một vùng cho thấy trong các vụ tai nạn ô tô có $0,37 \%$ người tử vong; $29 \%$ người không thắt dây an toàn và $0,28 \%$ người không thắt dây an toàn và tử vong. Chứng tỏ rằng việc không thắt dây an toàn khi lái xe và nguy cơ tử vong khi gặp tai nạn có liên quan với nhau.

Lời giải

Chọn ngẫu nhiên một người đã bị tai nạn ô tô.

Gọi $A$ là biến cố "Người đó đã tử vong"; $B$ là biến cố "Người đó đã không thắt dây an toàn".

Khi đó, $A B$ là biến cố "Người đó không thắt dây an toàn và đã tử vong".

Ta có $P(A)=0,37 \%=0,0037$; $P(B)=29 \%=0,29$; suy ra $P(A) P(B)=0,0037 . 0,29=0,001073$.

Mà $P(A B)=0,28 \%=0,0028$.

Vì $P(A B) \neq P(A) P(B)$ nên hai biến cố $A$ và $B$ không độc lập.

Vậy việc không thắt dây an toàn khi lái xe có liên quan tới nguy cơ tử vong khi gặp tai nạn.