Bài học cùng chủ đề
- Trường hợp đồng dạng thứ ba của tam giác (g.g)
- Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông
- Trường hợp đồng dạng đặc biệt của tam giác vuông
- Trường hợp đồng dạng thứ ba của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ ba của hai tam giác (nâng cao)
- Các trường hợp đồng dạng của hai tam giác vuông (cơ bản)
- Các trường hợp đồng dạng của hai tam giác vuông (vận dụng)
- Trường hợp bằng nhau thứ ba của hai tam giác
- Các trường hợp đồng dạng của hai tam giác vuông
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Các trường hợp đồng dạng của hai tam giác vuông (cơ bản) SVIP
Khẳng định nào sau đây sai?
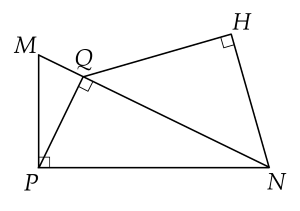
Cho hình vẽ.
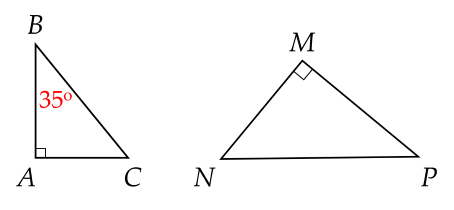
Để ΔABC∽ΔMPN (g-g) thì số đo góc N bằng
Cho hình vẽ, biết ΔABC∽ΔMNP.
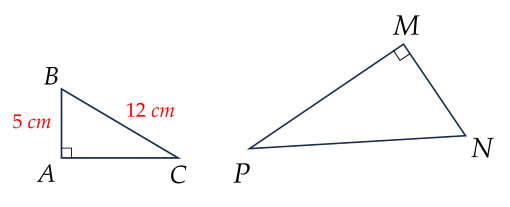
Tỉ số NPMN bằng
Cho ΔABC vuông tại A có C=50∘ và ΔDEF vuông tại D. Biết ΔABC∽ΔDEF.

Khi đó F bằng
Cho ΔABC vuông tại AC=4 cm, BC=6 cm. Kẻ tia Cx⊥BC (tia Cx và điểm A nằm ở hai phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho BD=9 cm.
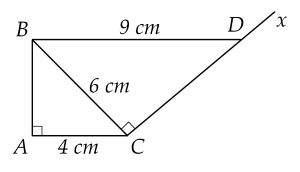
Khẳng định nào sau đây đúng?
Cho hình vẽ.
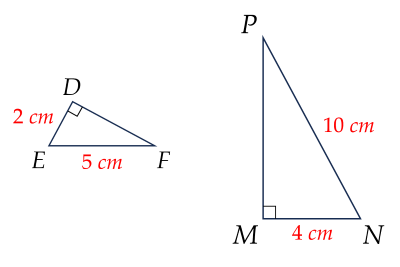
Khẳng định nào sau đây đúng?
Cho hình vẽ, khẳng định nào sau đây đúng?
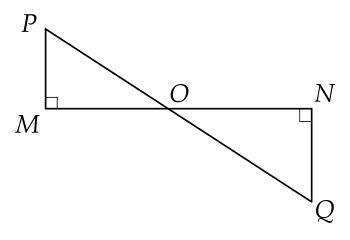
Cho hình vẽ:
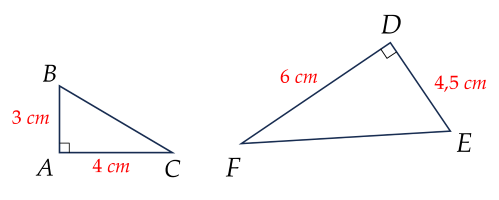
Khẳng định nào sau đây đúng?
Cho tam giác ABC vuông tại A. Lấy điểm D thuộc AB. Gọi H là hình chiếu vuông góc của D trên BC.
Khi đó, BH.BC= .
(Kéo thả hoặc click vào để điền)
Cho ba tam giác vuông sau:
Khẳng định nào dưới đây là đúng?
Cho tam giác ABC vuông tại A và tam giác MNP vuông tại M.
(Nhấp vào dòng để chọn đúng / sai)
| ΔABC∽ΔMNP khi AB.BC=MN.MP |
|
| ΔABC∽ΔMNP khi ACAB=MPMN. |
|
| ΔABC∽ΔMNP khi hai tam giác có thêm một cặp góc nhọn bằng nhau. |
|
Cho ΔABC vuông tại A; AB=3 cm, AC=4 cm và ΔDEF vuông tại D; DE=9 cm. Biết ΔABC∽ΔDEF.
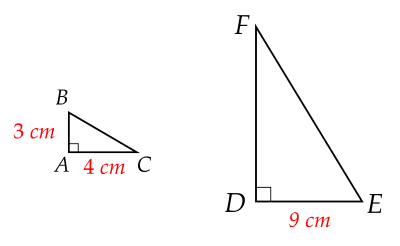
Khi đó độ dài DF bằng
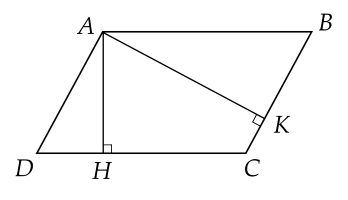
Cho hình bình hành ABCD, kẻ AH⊥CD tại H; AK⊥BC tại K.Khẳng định nào dưới đây đúng?
Cho hình thang vuông ABCD (AB // CD) có đường chéo BD vuông góc với cạnh BC tại B.
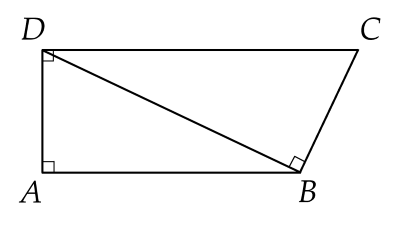
Khẳng định nào sau đây đúng?
Cho tam giác ABC vuông tại A, đường cao AH.
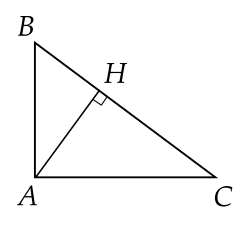
| ΔAHB∽ΔCHA. |
|
| AB2=BH.BC. |
|
| ΔABH∽ΔCBA. |
|
| AH=HB.HC. |
|


Bạn có thể đánh giá bài học này ở đây