Các phép toán trên tập hợp SVIP

1. HỢP VÀ GIAO CỦA CÁC TẬP HỢP

Cho hai tập hợp $A$ và $B$.

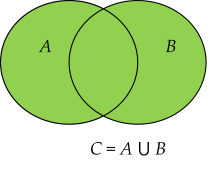
• Tập hợp các phần tử thuộc $A$ hoặc thuộc $B$ gọi là hợp của hai tập hợp $A$ và $B$, kí hiệu là $A \cup B$.

$A\cup B=\{x|x\in A$ hoặc $x\in B \}.$

• Tập hợp các phần tử thuộc cả hai tập hợp $A$ và $B$ gọi là giao của hai tập hợp $A$ và $B$, kí hiệu là ​$A\cap B$.

​$A\cap B=\{x|x\in A$​ và $x\in B \}.$

Ví dụ. Cho hai tập hợp \(X=\left\{1;3;5;7\right\}\);\(Y=\left\{x\inℤ|-2\le x< 4\right\}\). Tìm \(X\cap Y;X\cup Y\).

Giải

Ta có: \(Y=\left\{-2;-1;0;1;2;3\right\}\). Do đó:

 \(X\cap Y=\left\{1;3\right\}\);\(X\cup Y=\left\{-2;-1;0;1;2;3;5;7\right\}\).

Nhận xét:

• Nếu \(A\) và \(B\) là hai tập hợp hữu hạn thì \(n\left(A\cup B\right)=n\left(A\right)+n\left(B\right)-n\left(A\cap B\right).\) 
• Nếu  \(A\) và \(B\) không có phần tử chung, tức \(A\cap B=\varnothing\), thì \(n\left(A\cup B\right)=n\left(A\right)+n\left(B\right).\)

2. HIỆU CỦA HAI TẬP HỢP, PHẦN BÙ CỦA TẬP HỢP CON

Cho hai tập hợp \(A\) và \(B.\)

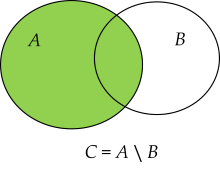
Tập hợp gồm các phần tử thuộc \(A\) nhưng không thuộc \(B\) được gọi là hiệu của \(A\) và \(B\), kí hiệu là \(A\setminus B\).

\(A\setminus B=\{x|x\in A\) và \(x\notin B\}\). 

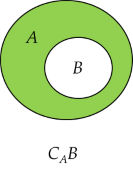
Nếu \(B\) là tập con của \(A\) thì hiệu \(A\setminus B\) gọi là phần bù của \(B\) trong \(A\), kí hiệu là \(C_AB\).

Ví dụ. Xác định tập hợp \(A=\left ( -3;2 \right )\setminus \left ( 1;4 \right )\) .

Giải

Để xác định tập \(A\), ta vẽ sơ đồ sau:

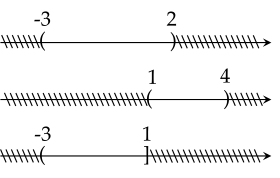
Khi đó \(A=(-3;1]\).