Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tự luận: Tam giác đồng dạng SVIP
Cho $A'$, $B'$, $C'$ nằm trên các cạnh $BC$, $AC$, $AB$ của $\Delta $ABC, biết $AA'$, $BB'$, $CC'$ đồng quy tại $M$. Chứng minh rằng $\dfrac{AM}{A'M}=\dfrac{AB'}{CB'}+\dfrac{AC'}{BC'}$.
Hướng dẫn giải:
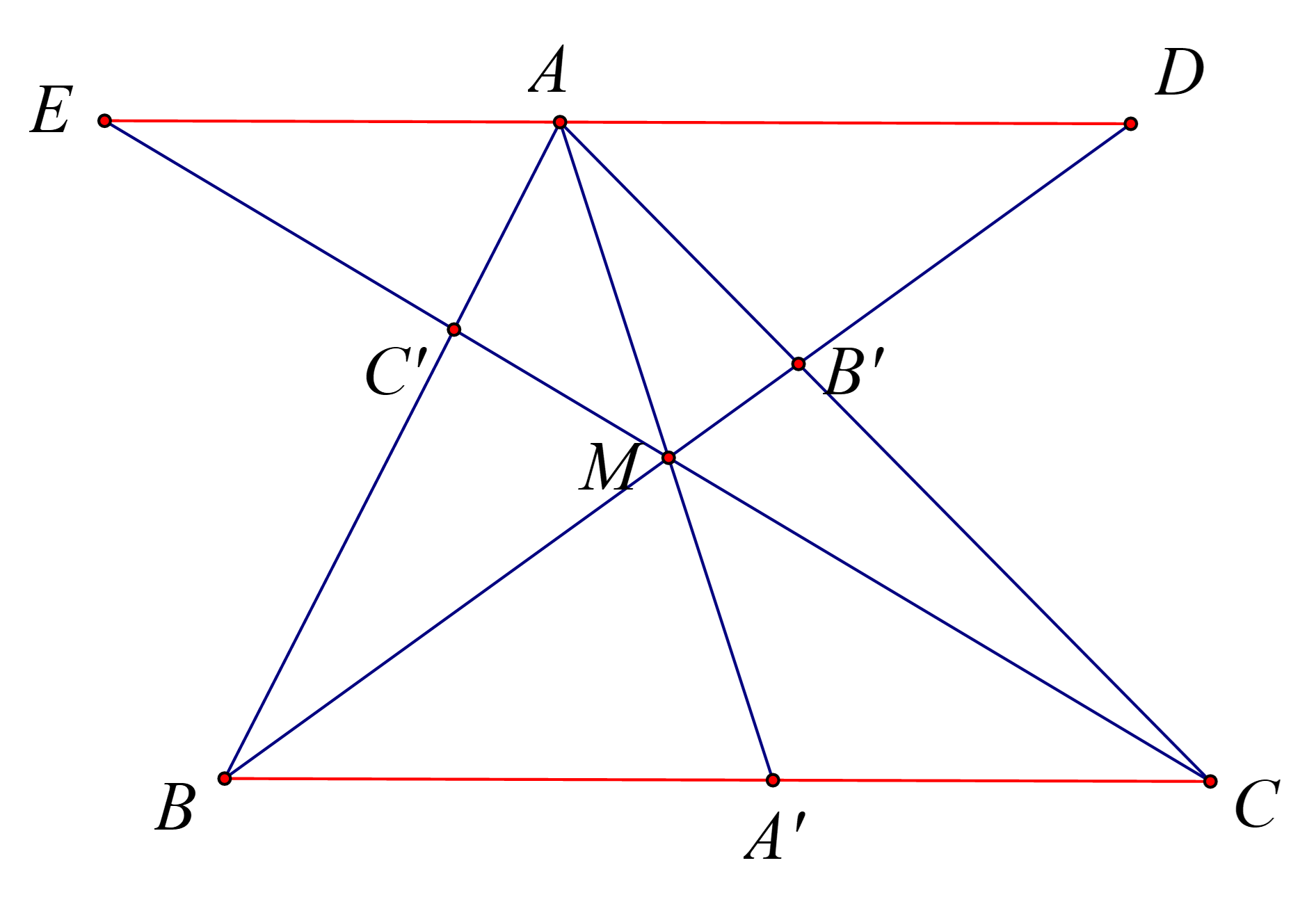
Qua $A$ vẽ đường thẳng song song với $BC$ cắt $BB'$ tại $D$ và cắt $CC'$ tại $E$.
Khi đó
$\Delta AME$ có $AE$ // $A'C$ suy ra $\dfrac{AM}{A'M}=\dfrac{AE}{A'C}$ (1)
$\Delta AMD$ có $AD$ // $A'B$ suy ra $\dfrac{AM}{A'M}=\dfrac{AD}{A'B}$ (2)
Từ (1) và (2) ta có $\dfrac{AM}{A'M}=\dfrac{AE}{A'C}=\dfrac{AD}{A'B}=\dfrac{AD+AE}{A'C+A'B}=\dfrac{DE}{BC}$ (*)
Chứng minh tương tự ta cũng có:
$\Delta AB'D$ có $AD$ // $BC$ suy ra $\dfrac{AB'}{B'C}=\dfrac{AD}{BC}$ (3)
$\Delta AC'E$ có $AE$ // $BC$ suy ra $\dfrac{AC'}{C'B}=\dfrac{AE}{BC}$ (4)
Từ (3) và (4) ta có $\dfrac{AB'}{B'C}+\dfrac{AC'}{BC'}=\dfrac{AD}{BC}+\dfrac{AE}{BC}=\dfrac{DE}{BC}$ (**)
Từ (*) và (**) ta có $\dfrac{AM}{A'M}=\dfrac{DE}{BC}=\dfrac{AB'}{B'C}+\dfrac{AC'}{BC'}$ (đpcm).
Cho hình bình hành $ABCD$ đường thẳng $a$ đi qua $A$ lần lượt cắt $BD$, $BC$, $DC$ tại $E$, $K$, $G$. Chứng minh rằng:
a) $AE^2=EK.EG$;
b) $\dfrac{1}{AE}=\dfrac{1}{AK}+\dfrac{1}{AG}$;
c) Khi $a$ thay đổi thì tích $BK.DG$ có giá trị không đổi?
Hướng dẫn giải:
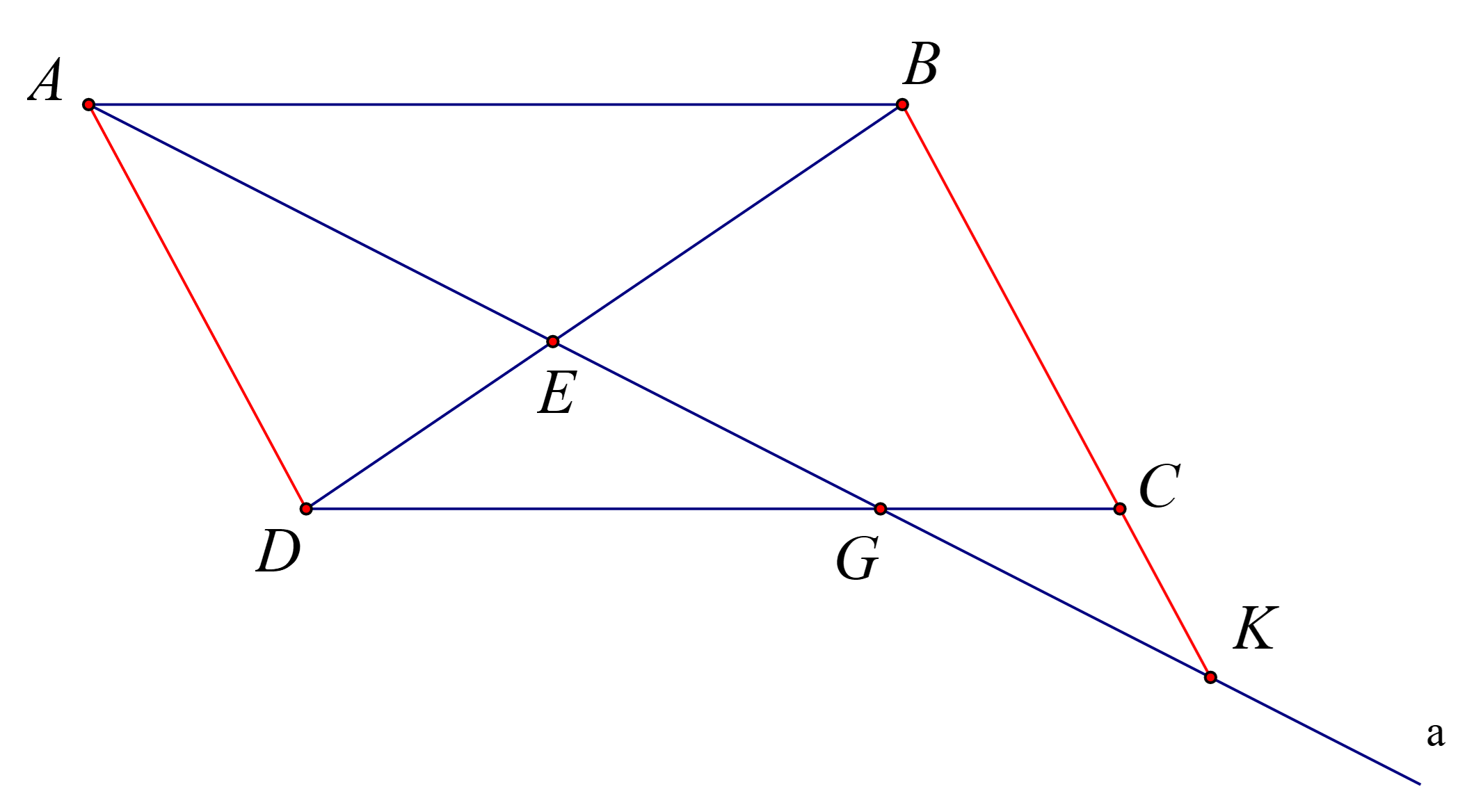
a) $\Delta ABE$ có $AM$ // $DG$ suy ra $\dfrac{AE}{EG}=\dfrac{EB}{ED}$ (1)
$\Delta ADE$ có $AD$ // $BK$ suy ra $\dfrac{EB}{ED}=\dfrac{EK}{EA}$ (2)
Từ (1) và (2) ta có $\dfrac{AE}{EG}=\dfrac{EK}{EA}$ nên $A{{E}^{2}}=EK.EG$.
b) Từ $\dfrac{1}{AE}=\dfrac{1}{AK}+\dfrac{1}{AG}$ suy ra $\dfrac{AE}{AK}+\dfrac{AE}{AG}=1$
$\Delta ADE$ có $AD$ // $BC$ suy ra $\dfrac{AE}{EK}=\dfrac{ED}{EB}$
$\dfrac{AE}{AE+EK}=\dfrac{ED}{ED+EB}$
$\dfrac{AE}{AK}=\dfrac{ED}{DB}$ (3)
Tương tự $\Delta AEB$ có $AB$ // $DG$ suy ra $\dfrac{AE}{EG}=\dfrac{BE}{ED}$
$\dfrac{AE}{AE+EG}=\dfrac{BE}{BE+ED}$
$\dfrac{AE}{AG}=\dfrac{BE}{BD}$ (4)
Khi đó $\dfrac{AE}{AK}+\dfrac{AE}{AG}=\dfrac{ED}{BD}+\dfrac{BE}{BD}=1$.
c) Ta có $\dfrac{BK}{KC}=\dfrac{AB}{CG}$ suy ra $BK=\dfrac{KC.AB}{CG}$ và $\dfrac{KC}{AD}=\dfrac{CG}{DG}$.
Suy ra $DG=\dfrac{AD.CG}{KC}$
Nhân theo vế ta được $BK.DG=AB.AD$ không đổi.
Cho hình thang $ABCD$ ($AB$ // $CD$) có $BC=BD$. Gọi $H$ là trung điểm của $CD$, đường thẳng đi qua $H$ cắt $AC$, $AD$ lần lượt tại $E$ và $ F$. Chứng minh rằng $\widehat{DBF}=\widehat{EBC}$.
Hướng dẫn giải:
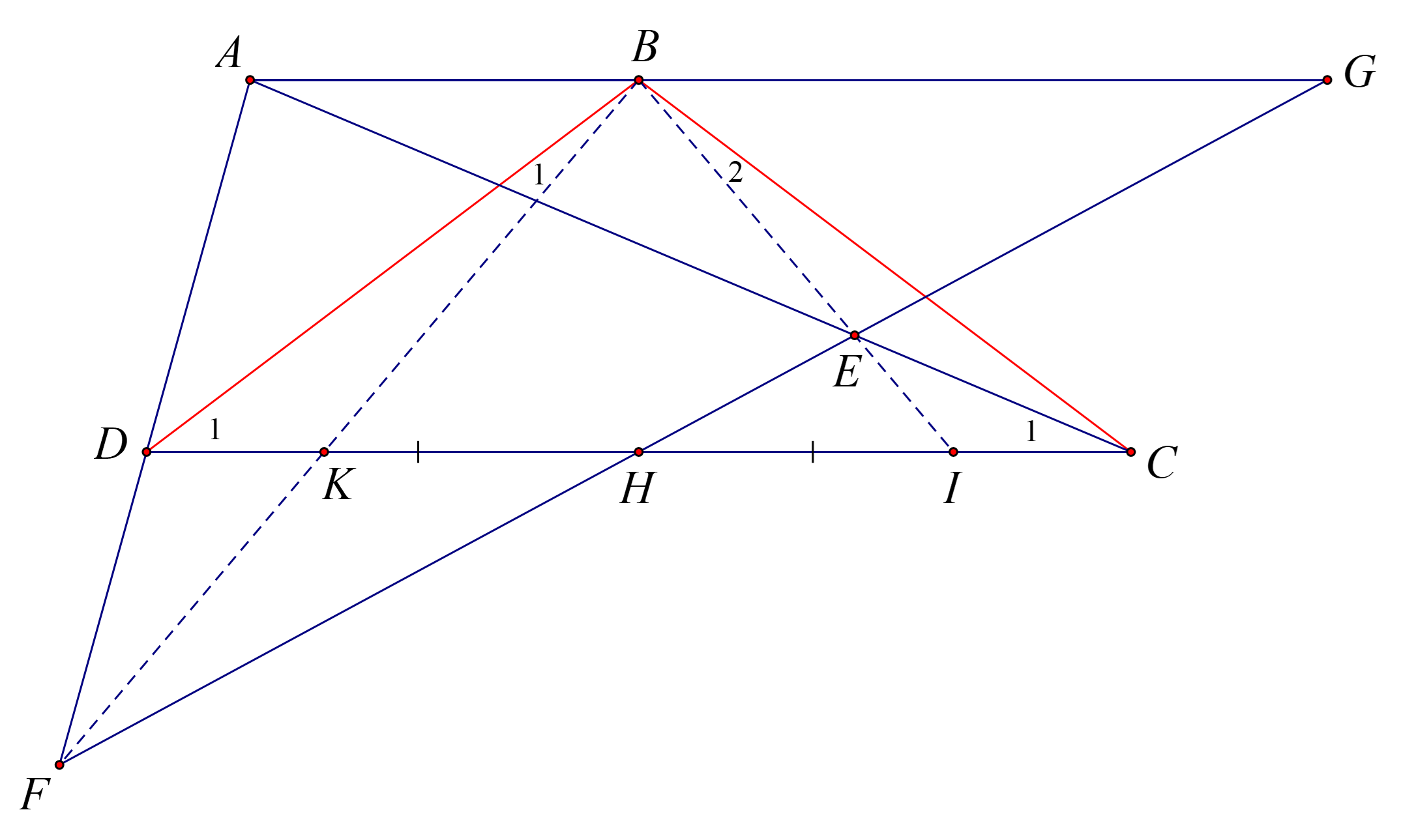
Gọi $BF$ cắt $DC$ tại $K$, $BE$ cắt $DC$ tại $I$, và $EF$ cắt $AB$ tại $G$.
$\Delta FAB$ có $DK$ // $AB$ suy ra $\dfrac{DK}{AB}=\dfrac{FD}{FA}$ (1)
$\Delta FAG$ có $DH$ // $AG$ suy ra $\dfrac{DH}{AG}=\dfrac{FD}{FA}$ (2)
Từ (1) và (2) suy ra $\dfrac{DK}{AB}=\dfrac{DH}{AG}$ hay $\dfrac{DK}{DH}=\dfrac{AB}{AG}$ (*)
Tương tự $\Delta EIC$ có $AB$ // $IC$ suy ra $\dfrac{IC}{AB}=\dfrac{EC}{EA}$ (3)
$\Delta EHC$ có $HC$ // $AB$ suy ra $\dfrac{HC}{AG}=\dfrac{EC}{EA}$ (4)
Từ (3) và (4) ta có $\dfrac{IC}{AB}=\dfrac{HC}{AG}$ hay $\dfrac{IC}{HC}=\dfrac{AB}{AG}$ (**)
Từ (*) và (**) ta có $\dfrac{DK}{DH}=\dfrac{IC}{HC}$.
Mà $DH=HC$ (gt) suy ra $DK=IC$
Mặt khác $BD=BC$ (gt) nên $\Delta BDC$ cân
Suy ra $\widehat{BDK}=\widehat{BCI}$
Vậy $\Delta BDK=\Delta BCI$ (c.g.c)
Suy ra $\widehat{DBK}=\widehat{CBI}$.
Cho tam giác $ABC$ nhọn, trên các đường cao $BE$, $CF$ lấy các điểm theo thứ tự $I$, $K$ sao cho $\widehat{AIC}=90^\circ, \, \widehat{AKB}=90^\circ$
a) Chứng minh $AI=AK$.
b) Cho $\widehat{A}=60^\circ, \, S_{ABC}=120$ cm$^{2}$, Tính diện tích tam giác $AEF$.
Hướng dẫn giải:
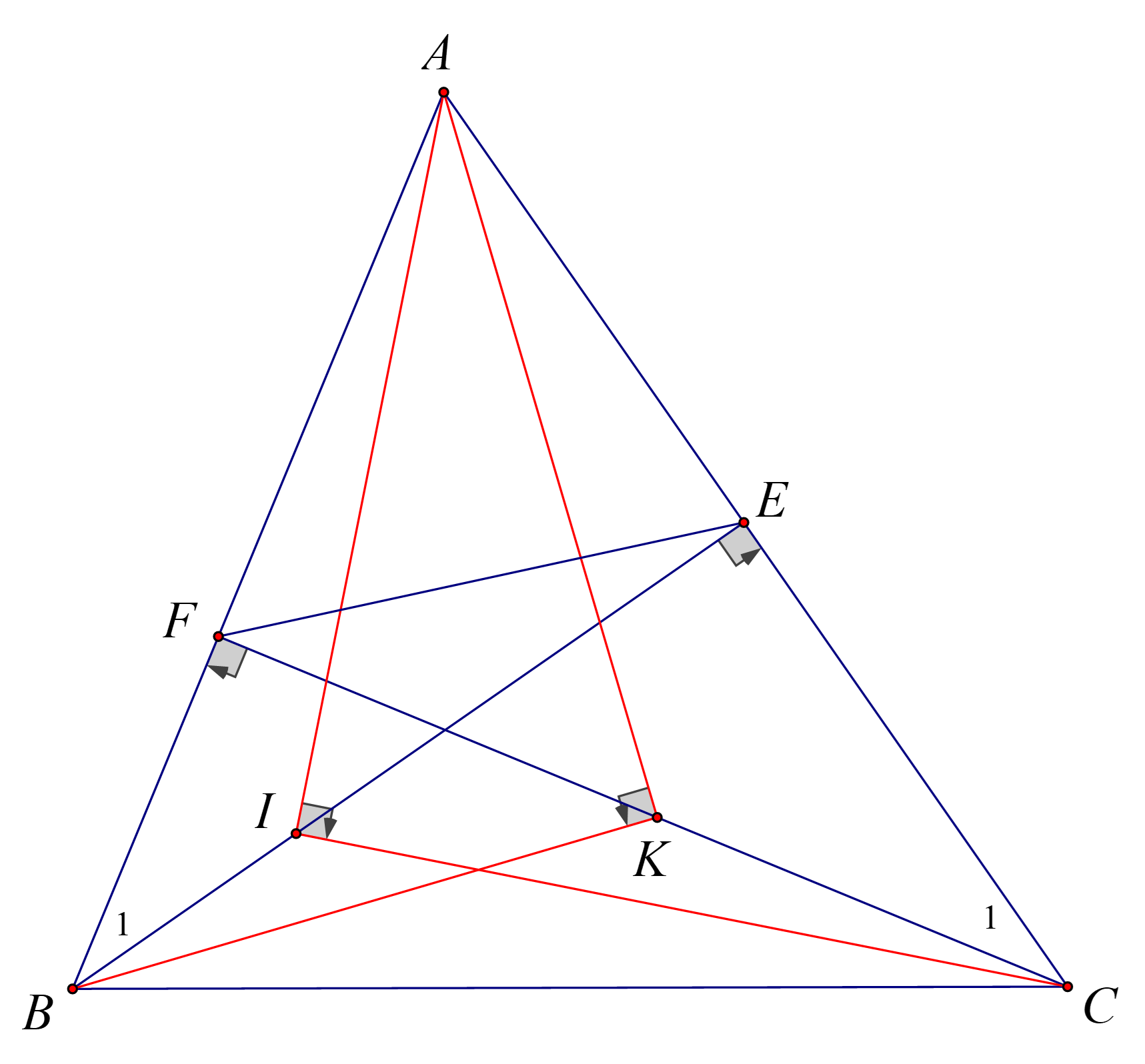
a) $\Delta AIE \backsim \Delta ACI$ (g.g) suy ra $\dfrac{AI}{AC}=\dfrac{AE}{AI}$ hay $A{{I}^{2}}=AE.AC$ (1)
Chứng minh tương tự:
$\Delta AIK \backsim \Delta AKB$ (g.g) suy ra $\dfrac{AK}{AB}=\dfrac{AF}{AK}$ hay $A{{K}^{2}}=AB.AF$ (2)
Mà $\Delta ABE \backsim \Delta ACF$ (g.g) suy ra $\dfrac{AB}{AC}=\dfrac{AE}{AF}$ hay $AB.AF=AC.AE$ (3)
Từ (1), (2) và (3) ta có $A{{I}^{2}}=A{{K}^{2}}$ suy ra $AI=AK$.
b) Vì $\widehat{A}={{60}^\circ}$ suy ra $\widehat{{{B}_{1}}}={{30}^\circ}$
Trong tam giác $ABE$ vuông tại $E$ nên $AE=\dfrac{1}{2}AB,$
Trong tam giác $AFC$ vuông tại $F$ có $\widehat{{{C}_{1}}}={{30}^\circ}$ suy ra $AF=\dfrac{1}{2}AC$.
Do đó, $\Delta AEF \backsim \Delta ABC$ (c.g.c).
suy ra $\dfrac{{{S}_{AEF}}}{{{S}_{ABC}}}={{\left( \dfrac{AE}{AB} \right)}^{2}}=\dfrac{1}{4}$.
Vậy ${{S}_{AEF}}=\dfrac{1}{4}.120=30$ cm$^{2}$.
