Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tự luận: Hình vuông SVIP
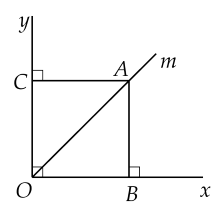
Cho $\widehat{xOy}={{90}^{\circ}}$ và tia phân giác $Om$. Lấy điểm $A$ trên $Om.$ Kẻ $AB, \, AC$ lần lượt vuông góc với $Ox, \, Oy\,.$ Chứng minh $OBAC$ là hình vuông.
Hướng dẫn giải:

Tứ giác $OBAC$ có ba góc vuông $\widehat{B\,}=\widehat{C\,}=\widehat{BOC\,}={{90}^{\circ}}$
Nên $OBAC$ là hình chữ nhật.
Mà $A$ nằm trên tia phân giác $OM$ suy ra $AB=AC$.
Khi đó $OBAC$ là hình vuông.
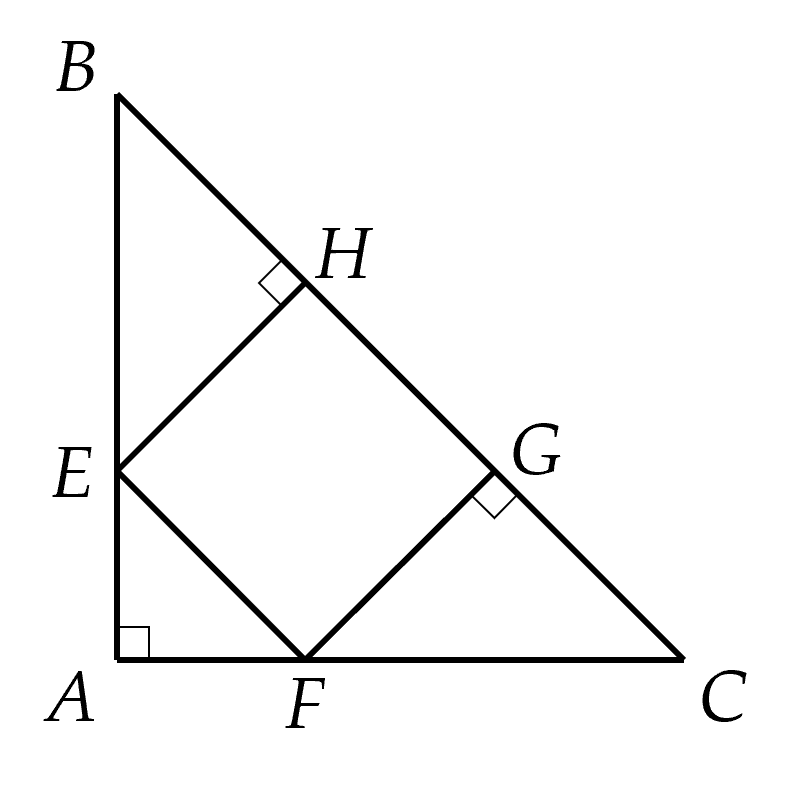
Cho $\Delta ABC$ vuông cân tại $A$. Trên cạnh $BC$ lấy hai điểm $H, \, G$ sao cho $BH=HG=GC\,.$ Qua $H$ và $G$ kẻ các đường thẳng vuông góc với $BC$ chúng cắt $AB, \, AC$ lần lượt tại $E, \, F.$
a) Chứng minh $\Delta BHE$ là tam giác vuông cân.
b) Chứng minh tứ giác $EFGH$ là hình vuông.
Hướng dẫn giải:
a) $\Delta ABC$ vuông cân nên $\widehat{B\,}=\widehat{C\,}={{45}^{\circ}}.$
$\Delta BHE$ vuông tại $H$ có $\widehat{BEH}+\widehat{B\,}={{90}^{\circ}}$
Suy ra $\widehat{BEH\,}={{90}^{\circ}}-{{45}^{\circ}}={{45}^{\circ}}$ nên $\widehat{B\,}=\widehat{BEH}={{45}^{\circ}}$.
Vậy $\Delta BEH$ vuông cân tại $H.$
b) Chứng minh tương tự câu a ta được $\Delta CFG$ vuông cân tại $G$ nên $GF=GC$ và $HB=HE$
Mặt khác $BH=HG=GC$ suy ra $ EH=HG=GF$ và $EH$ // $FG$ (cùng vuông góc với $BC)$
Tứ giác $EFGH$ có $EH$ // $FG, \, EH=FG$ nên là hình bình hành.
Hình bình hành $EFGH$ có một góc vuông $\widehat{H}$ nên là hình chữ nhật
Hình chữ nhật $EFGH$ có hai cạnh kề bằng nhau $EH=HG$ nên là hình vuông.
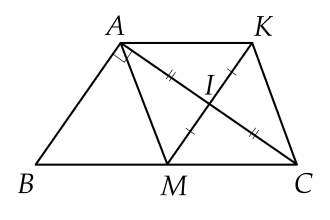
Cho $\Delta ABC$ vuông tại $A,$ đường trung tuyến $AM.$ Gọi $I$ là trung điểm của $AC$. Trên tia đối của tia $IM$ lấy điểm $K$ sao cho $IK=IM.$
a) Chứng minh $AMCK$ là hình thoi.
b) Chứng minh $AKMB$ là hình bình hành.
c) Tìm điều kiện của $\Delta ABC$ để tứ giác $AMCK$ là hình vuông.
Hướng dẫn giải:
a) Tứ giác $AMCK$ có hai đường chéo $AC, \, MK$ cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
$\Delta ABC$ vuông tại $A$ có $AM$ là đường trung tuyến nên $AM=MC=MB$.
Vậy hình bình hành $AMCK$ có $AM=MC$ nên là hình thoi.
b) Vì $AMCK$ là hình thoi nên $AK$ // $BM$ và $AK=MC=BM$.
Tứ giác $AKMB$ có $AK$ // $BM, \, AK=BM$ nên là hình bình hành.
c) Để $AMCK$ là hình vuông thì cần có một góc vuông hay $AM\bot MC$.
Khi đó $\Delta ABC$ có $AM$ vừa là đường cao vừa là đường trung tuyến nên cân tại $A$.
Vậy $\Delta ABC$ vuông cân tại $A$ thì $AMCK$ là hình vuông.
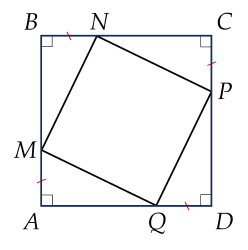
Cho hình vuông $ABCD$. Trên các cạnh $AB, \, BC,$ $CD, \, DA$ lấy lần lượt các điểm $M, \, N, \, P, \, Q$ sao cho $AM=BN=CP=DQ.$
a) Chứng minh $MB=NC=PD=QA.$
b) Chứng minh $\Delta QAM=\Delta NCP.$
c) Chứng minh $MNPQ$ là hình vuông.
Hướng dẫn giải:
a) $ABCD$ là hình vuông nên $AB=BC=CD=DA$
Mà $AM=BN=CP=DQ$.
Trừ theo vế ta được $AB-AM=BC-BN=CD-CP=DA-DQ$
Suy ra $MB=NC=PD=QA$
b) Xét $\Delta QAM$ và $\Delta NCP$ có:
$\widehat{A}=\widehat{C}={{90}^{\circ}}$
$AQ=NC$ (chứng minh trên)
$AM=CP$ (giả thiết)
Suy ra $\Delta QAM=\Delta NCP$ (c.g.c)
c) Từ $\Delta QAM=\Delta NCP$ suy ra $NP=MQ$ (hai cạnh tương ứng).
Chứng minh tương tự câu b ta có $\Delta QAM=\Delta PDQ$ và $\Delta QAM=\Delta MBN$.
Khi đó $\Rightarrow MQ=PQ, \, MN=MQ$ và $\widehat{AMQ}=\widehat{DQP}$.
Mà $\widehat{AMQ}+\widehat{AQM}={{90}^{\circ}}$ suy ra $\widehat{DQP}+\widehat{AQM}={{90}^{\circ}}$.
Do đó, $\widehat{MQP}={90}^{\circ}$.
Tứ giác $MNPQ$ có bốn cạnh bằng nhau nên là hình thoi, lại có $\widehat{MQP}={{90}^{\circ}}$ nên là hình vuông.
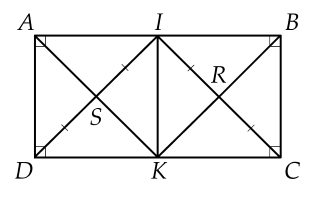
Cho hình chữ nhật $ABCD$ có $AB=2BC.$ Gọi $I$ là trung điểm của $AB$ và $K$ là trung điểm của $DC.$
a) Chứng minh $AIKD$ và $BIKC$ là hình vuông.
b) Chứng minh $\Delta DIC$ vuông cân.
c) Gọi $S$ và $R$ lần lượt là tâm các hình vuông $AIKD,$ $BIKC.$ Chứng minh $[ISKR$ là hình vuông.
Hướng dẫn giải:
a) Vì $AB=2BC$ suy ra $BC=\dfrac{AB}{2}=AD$
$ABCD$ là hình chữ nhật nên $AB=DC$ suy ra $\dfrac{1}{2}AB=\dfrac{1}{2}DC$ do đó $AI=DK=AD$.
Tứ giác $AIKD$ có $AI$ // $DK, \, AI=DK$ nên $AIKD$ là hình bình hành.
Lại có $AD=AI$ nên $AIKD$ là hình thoi.
Mà $\widehat{IAD}={{90}^{\circ}}$ do đó $AIKD$ là hình vuông.
Chứng minh tương tự cho tứ giác $BIKC$
b) Vì $AIKD$ là hình vuông nên $DI$ là tia phân giác $\widehat{ADK}$ hay $\widehat{IDK}={{45}^{\circ}}$.
Tương tự $\widehat{ICD}={{45}^{\circ}}$.
$\Delta IDC$ cân có $\widehat{DIC}={{90}^{\circ}}$ nên là tam giác vuông cân.
c) Vì $AIKD, \, BCKI$ là các hình vuông nên hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên $SI=SK=\dfrac{DI}{2}$ và $IR=RK=\dfrac{IC}{2}$
Suy ra $ISKR$ là hình thoi.
Lại có $\widehat{DIC}={{90}^{\circ}}$ nên $ISKR$ là hình vuông.
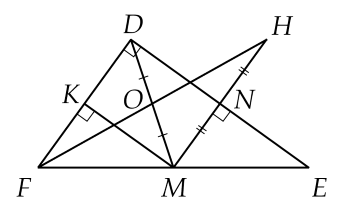
Cho $\Delta DEF$ vuông tại $D$ có $DE>DF.$ $DM$ là đường trung tuyến. Gọi $MN$ là đường vuông góc kẻ từ $M$ đến $DE$, $MK$ là đường vuông góc kẻ từ $M$ đến $DF.$ Trên tia $MN$ lấy $H$ sao cho $N$ là trung điểm của $MH.$
a) Tứ giác $DKMN$ là hình gì? Tại sao?
b) Gọi $O$ là trung điểm của $DM.$ Chứng minh $3$ điểm $H, \, O, \, F$ thẳng hàng.
c) $\Delta DEF$ cần thêm điều kiện gì để tứ giác $DKMN$ là hình vuông.
Hướng dẫn giải:
a) Tứ giác $DKMN$ có $\widehat{D}=\widehat{K}=\widehat{N}={{90}^{\circ}}$ nên là hình chữ nhật.
b) Vì $DKMN$ là hình chữ nhật nên $DF$ // $MH$
Xét $\Delta KFM$ và $\Delta NME$ có:
$\widehat{K}=\widehat{N}={{90}^{\circ}}$
$FM=ME$ ( giả thiết)
$\widehat{KMF}=\widehat{E}$ (đồng vị)
Vậy $\Delta KFM=\Delta NME$ (cạnh huyền - góc nhọn)
Suy ra $KF=MN$ (hai cạnh tương ứng) mà $MN=DK$ nên $DF=2DK$ và $MH=2MN$.
Do đó $DF=MH$.
Tứ giác $DFMH$ có $DF$ // $MH, \, DF=MH$ nên là hình bình hành.
Do đó, hai đường chéo $DM, \, FH$ cắt nhau tại trung điểm $O$ của mỗi đường hay $F, \, O, \, H$ thẳng hàng.
c) Để hình chữ nhật $DKMN$ là hình vuông thì $DK=DN$ $\left( 1 \right)$
Mà $DK=\dfrac{1}{2}DF$ và $DN=KM=NE$ nên $DN=\dfrac{1}{2}DE$ $\left( 2 \right)$
Từ $\left( 1 \right), \, \left( 2 \right)$ suy ra $DF=DE$.
Vậy $\Delta DFE$ cần thêm điều kiên cân tại $D$.
