Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tự luận: Hình thoi SVIP
Cho hình thoi $ABCD$. Lấy $E, \, F$ trên $BC$ và $CD$ sao cho $BE=DF.$ Gọi $G, \, H$ lần lượt là giao điểm của $AE, \, AF$ với $BD.$ Chứng minh $AGCH$ là hình thoi.
Hướng dẫn giải:
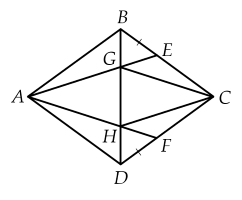
Ta có $ABCD$ là hình thoi nên $AC\bot BD$ tại trung điểm của mỗi đường nên $BD$ là trung trực của $AC$
Suy ra $GA=GC, \, HA=HC$ $\left( 1 \right)$
Và $AC$ là trung trực của $BD$ suy ra $AG=AH, \, CG=CH$ $\left( 2 \right)$
Từ $\left( 1 \right), \, \left( 2 \right)$ suy ra $AG=GC=CH=HA$ nên $AGCH$ là hình thoi.
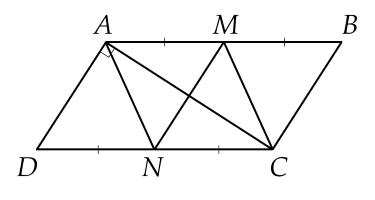
Cho hình bình hành $ABCD$ có $AD\bot AC\,.$ Gọi $M, \, N$ lần lượt là trung điểm của $AB, \, CD.$
a) Chứng minh $MN\bot AC.$
b) Tứ giác $AMCN$ là hình gì?
Hướng dẫn giải:
a) $ABCD$ là hình bình hành nên $AB=DC$ suy ra $\dfrac{1}{2}AB=\dfrac{1}{2}DC$
Do đó $AM=BM=DN=CN$.
Tứ giác $AMCN$ có $AM$ // $NC, \, AM=NC$ nên là hình bình hành.
Lại có $\Delta ADC$ vuông tại $A$ có $AN$ là đường trung tuyến nên $AN=\dfrac{1}{2}DC=DN=CN$.
Hình bình hành $AMCN$ có hai cạnh kề bằng nhau nên là hình thoi, khi đó hai đường chéo $AC, \, MN$ vuông góc với nhau.
Tứ giác $AMCN$ là hình thoi.
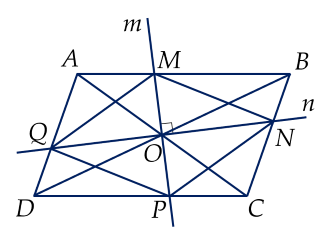
Cho hình bình hành $ABCD$. Hai đường chéo $AC, \, BD$ cắt nhau tại $O.$ Đường thẳng $m$ đi qua $O$ cắt $AB, \, CD$ lần lượt tại $M$ và $P.$ Đường thẳng $n$ đi qua $O$ và vuông góc với $m$ cắt cạnh $BC$ và $DA$ lần lượt tại $N$ và $Q.$
a) Chứng minh $MNPQ$ là hình bình hành.
b) Chứng minh $MNPQ$ là hình thoi.
Hướng dẫn giải:
a) $ABCD$ là hình bình hành nên hai đường chéo $AC, \, BD$ cắt nhau tại $O$ là trung điểm của mỗi đường.
Xét $\Delta OBM$ và $\Delta ODP$ có:
$OB=OD$ ( giả thiết)
$\widehat{OBM}=\widehat{ODP}$ (so le trong)
$\widehat{BOM}=\widehat{DOP}$ (đối đỉnh)
Vậy $\Delta OBM=\Delta ODP$ (g.c.g)
Suy ra $OM=OP$ (hai cạnh tương ứng)
Chứng minh tương tự $\Delta OAQ=\Delta OCN$ (g.c.g) suy ra $OQ=ON$ (hai cạnh tương ứng)
$MNPQ$ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Hình bình hành $MNPQ$ có hai đường chéo $MP\bot NQ$ nên là hình thoi.
