Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tự luận: Tứ giác SVIP
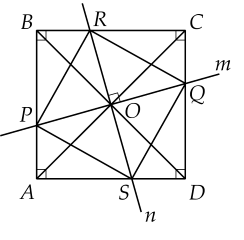
Cho hình vuông $ABCD.$ $O$ là giao điểm của hai đường chéo. Hai đường thẳng $m, \, n$ vuông góc với nhau tại $O$. Đường thẳng $m$ cắt $AB, \, CD$ lần lượt tại $P, \, Q.$ Đường thẳng $n$ cắt $BC, \, AD$ lần lượt ở $R, \, S\,.$
a) Chứng minh $\Delta AOP=\Delta BOR.$
b) Chứng minh $OP=OR=OS=OQ.$
c) Chứng minh $PRQS$ là hình vuông.
Hướng dẫn giải:
a) Ta có $\widehat{{{O}_{1}}}+\widehat{{{O}_{3}}}={{90}^{\circ}}$ và $\widehat{{{O}_{2}}}+\widehat{{{O}_{3}}}={{90}^{\circ}}$ suy ra $\widehat{{{O}_{1}}}=\widehat{{{O}_{2}}}$.
Mặt khác $\widehat{{{A}_{1}}}=\widehat{{{B}_{1}}}={{45}^{\circ}}$.
Xét $\Delta AOP$ và $\Delta BOR$ có
$OA=OB$ ( giả thiết)
$\widehat{A_1}=\widehat{B_1}=45^\circ$
$\widehat{O_1}=\widehat{O_2}$ (chứng minh trên)
Suy ra $\Delta AOP=\Delta BOR$ (g.c.g)
b) Từ $\Delta AOP=\Delta BOR$ suy ra $OP=OR$ (hai cạnh tương ứng)
Chứng minh tương tự cho $\Delta OBR=\Delta OCQ$ và $\Delta OCQ=\Delta ODS$
Suy ra $OR=OQ$ và $OQ=OS$.
Khi đó $OP=OR=OS=OQ.$
c) Tứ giác $PRQS$ là hình thoi vì có bốn cạnh bằng nhau.
Mà $\Delta OPR$ có $OP=OR$ và $\widehat{POR}={{90}^{\circ}}$ nên $\Delta OPR$ là tam giác vuông cân tại $O$
Suy ra $\widehat{{{P}_{1}}}={{45}^{\circ}}$.
Tương tự $\widehat{{{P}_{2}}}={{45}^{\circ}}$ nên $\widehat{RPS}=\widehat{{{P}_{1}}}+\widehat{{{P}_{2}}}={{90}^{\circ}}$.
Hình thoi $PRQS$ có $\widehat{RPS}={{90}^{\circ}}$ nên nó là hình vuông.
Cho hình bình hành $ABCD$ có $\widehat{BAD}={{60}^{\circ}}$ và $AD=2AB.$ Gọi $M$ là trung điểm của $BC,$ $N$ là trung điểm của $AD.$
a) Chứng minh $MCDN$ là hình thoi.
b) Chứng minh $ABMD$ là hình thang cân và $AM=BD.$
c) $DM$ kéo dài cắt $AB$ tại $K.$ Chứng minh $AM, \, DB, \, KN$ đồng quy.
Hướng dẫn giải:
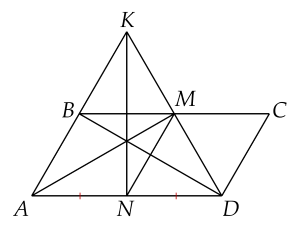
a) Ta có $AD=BC$ suy ra $\dfrac{AD}{2}=\dfrac{BC}{2}$ nên $MC=ND$ và $MC$ // $ND$
Do đó, $MCDN$ là hình bình hành.
Lại có $CD=AB=\dfrac{AD}{2}=ND$ nên $MCDN$ là hình thoi
b) $BM$ // $AD$ suy ra $ABMD$ là hình thang.
Mà $\widehat{ADC}={{120}^{\circ}}$ mà $DM$ là phân giác $\widehat{ADC}$ nên $\widehat{ADM}={{60}^{\circ}}=\widehat{BAD}$.
Vậy $ABMD$ là hình thang cân.
c) $\Delta KAD$ có $\widehat{KAD}=\widehat{KDA}$ nên là tam giác cân.
Xét $\Delta MBK$ và $\Delta MCD$ có:
$MB=MC$ (giả thiết)
$\widehat{{{M}_{1}}}=\widehat{{{M}_{2}}}$ (đối đỉnh)
$\widehat{{{B}_{1}}}=\widehat{C}$ (so le trong)
Vậy $\Delta MBK=\Delta MCD$ (g.c.g) suy ra $ MK=MD$ (hai cạnh tương ứng).
Khi đó $AM$ là đường trung tuyến và $BK=CD$ (hai cạnh tương ứng)
Mà $CD=AB$ suy ra $AB=BK$ hay $DB$ là đường trung tuyến.
Khi đó, $\Delta KAD$ có ba đường trung tuyến $AM, \, BD, \, KN$ đồng quy.
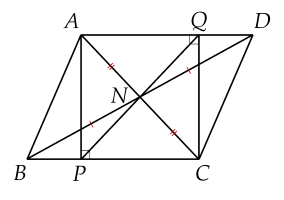
Cho $\Delta ABC$ nhọn có $AB<AC.$ Gọi $N$ là trung điểm của $AC.$ Lấy điểm $D$ trên tia $BN$ sao cho $BN=ND.$
a) Chứng minh $ABCD$ là hình bình hành.
b) Kẻ $AP\bot BC, \, CQ\bot AD.$ Chứng minh $P, \, N, \, Q$ thẳng hàng.
c) $\Delta ABC$ cần thêm điều kiện gì để tứ giác $ABCD$ là hình vuông.
Hướng dẫn giải:
a) Tứ giác $ABCD$ có hai đường chéo $AC, \, BD$ cắt nhau tại trung điểm $N$ của mỗi đường nên là hình bình hành.
b) Ta có $AP\bot BC$; $AQ$ // $BC$ suy ra $AP\bot AQ$.
Tứ giác $APCQ$ có ba góc vuông nên là hình chữ nhật.
Khi đó hai đường chéo $AC, \, PQ$ cắt nhau tại trung điểm của mỗi đường, mà $NA=NC$ nên $N$ là trung điểm của $PQ$.
Suy ra $P, \, N, \, Q$ thẳng hàng.
c) Để tứ giác $ABCD$ là hình vuông thì ta cần $AB\bot BC, \, AB=BC$ hay $\Delta ABC$ vuông cân tại $B.$
Cho $\Delta ABC$ vuông tại $A,$ trung tuyến $AM.$ Kẻ $MD\bot AB$ tại $D,$ $ME\bot AC$ tại $E.$
a) Chứng minh $ADME$ là hình chữ nhật.
b) Lấy điểm $I$ sao cho $D$ là trung điểm của $IM$.Tứ giác $AMBI$ là hình gì?
c) Tìm điều kiện của $\Delta ABC$ để tứ giác $AMBI$ là hình vuông.
d) Vẽ đường cao $AH$ của $\Delta ABC,$ kẻ $HP\bot AB$, $HQ\bot AC.$ Chứng minh $PQ\bot AM.$
Hướng dẫn giải:
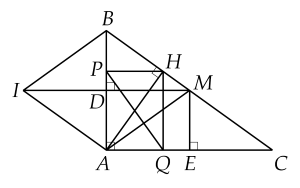
a) Tứ giác $ADME$ có $\widehat{DAE}=\widehat{D}=\widehat{E}={{90}^{\circ}}$ nên $ADME$ là hình chữ nhật.
b) Vì $DM\bot AB $ và $AC\bot AB$ nên $DM$ // $AC$ suy ra $\widehat{C}=\widehat{BMD}$ (so le trong).
Xét $\Delta DMB$ và $\Delta ECM$ có:
$\widehat{D}=\widehat{E}={{90}^{\circ}}$
$BM=CM$ (giả thiết)
$\widehat{DMB}=\widehat{C}$ (so le trong)
Vậy $\Delta DMB=\Delta ECM$ (cạnh huyền - góc nhọn)
Suy ra $ME=BD$ (hai cạnh tương ứng) mà $ME=AD$ nên $AD=BD$.
Tứ giác $AMBI$ có hai đường chéo $AB, \, MI$ cắt nhau tại $D$ là trung điểm của mỗi đường nên là hình bình hành.
Mà $MI\bot AB$ suy ra $AMBI$ là hình thoi.
c) Để $AMBI$ là hình vuông thì $AM\bot BM$ hay $AM$ vừa là đường trung tuyến vừa là đường cao nên $\Delta ABC$ vuông cân tại $A.$
d) Giả sử $AM$ cắt $PQ$ tại $F$ và $PQ$ cắt $AH$ tại $O$.
Khi đó $\Delta OAQ$ có $OA=OQ$ nên $ \Delta OAQ$ cân tại $O$ suy ra $ \widehat{{{Q}_{1}}}=\widehat{OAQ}$
$\Delta AMC$ cân tại $M$ suy ra $\widehat{{{A}_{1}}}=\widehat{C\,}$
Do đó, $\widehat{{{A}_{1}}}+\widehat{{{Q}_{1}}}=\widehat{C}+\widehat{OAQ}={{90}^{\circ}}$
Suy ra $\Delta FAQ$ vuông tại $F$ hay $AM\bot PQ.$
Cho $\Delta ABC$ vuông cân tại $A.$ Gọi $M$ là trung điểm của $BC.$ Trên tia đối của tia $MA$ lấy điểm $D$ bất kì. Từ $D$ kẻ các đường thẳng vuông góc với $AB, \, AC$ lần lượt tại $E, \, F.$
a) Chứng minh $AEDF$ là hình vuông.
b) Chứng minh $EF$ // $BC.$
c) Qua $E$ kẻ đường thẳng vuông góc với $MF$ tại $N.$ Chứng minh $\widehat{AND}={{90}^{\circ}}.$
Hướng dẫn giải:
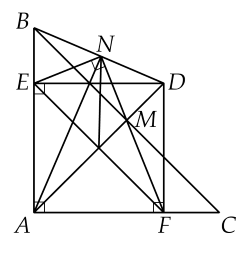
a) Tứ giác $AEDF$ có $\widehat{EAF}=\widehat{AED}=\widehat{AFD}={{90}^{\circ}}$ nên là hình chữ nhật.
$\Delta ABC$ vuông cân tại $A$ có $AM$ là trung tuyến nên $AM$ cũng là đường phân giác $\widehat{EAF}$.
Hình chữ nhật $AEDF$ có đường chéo $AD$ là tia phân giác $\widehat{EAF}$ nên là hình vuông.
b) $\Delta AEF$ vuông tại $A$ có $AE=AF$ nên vuông cân tại $A$
Suy ra $ \widehat{{{F}_{1}}}={{45}^{\circ}}=\widehat{C}$ mà $\widehat{{{F}_{1}}}, \, \widehat{C}$ đồng vị nên $EF$ // $BC.$
c) Gọi $O$ là giao của $AD$ với $EF$ suy ra $OE=OD=OF=OA$
$\Delta ENF$ vuông tại $N$ có $NO$ là đường trung tuyến nên $NO=EO=FO$
$\Delta AND$ có $NO$ là đường trung tuyến mà $NO=\dfrac{AD}{2}$ suy ra $\Delta AND$ vuông tại $N.$
