Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tổng hợp SVIP
Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$, điểm $M$ thuộc cung $BC$ không chứa $A$. Vẽ $MH$ vuông góc với $AB$ tại $H$ và $MK$ vuông góc với $AC$ ở $K$.
a/ Chứng minh tứ giác $AHMK$ nội tiếp.
b/ Chứng minh \(\Delta MHK \backsim\Delta MBC\).
c/ Giả sử $HK$ cắt $BC$ tại $G$. Chứng minh \(MG\perp BC\).
Hướng dẫn giải:

a) Do MH và MK là các đường cao nên \(\widehat{AKM}=\widehat{AHM}=90^o\).
Xét tứ giác AHMK có \(\widehat{AHM}+\widehat{AKM}=180^o\) nên tứ giác AHMK nội tiếp.
b) Do AHMK nội tiếp nên \(\widehat{MHK}=\widehat{MAK}\) (Hai góc nội tiếp cùng chắn cung MK)
Lại có \(\widehat{MAK}=\widehat{MAC}=\widehat{MBC}\) (Hai góc nội tiếp cùng chắn cung MC)
Nên \(\widehat{MHK}=\widehat{MBC}\).
Do AHMK nội tiếp nên \(\widehat{HKM}=\widehat{HAM}\) (Hai góc nội tiếp cùng chắn cung HM)
Lại có \(\widehat{HAM}=\widehat{BAM}=\widehat{BCM}\) (Hai góc nội tiếp cùng chắn cung MC)
Nên \(\widehat{HKM}=\widehat{BCM}\).
Xét tam giác HMK và tam giác BMC có \(\widehat{MHK}=\widehat{MBC}\) và \(\widehat{HKM}=\widehat{BCM}\) nên \(\Delta HMK\backsim\Delta BMC\left(g-g\right)\)
c) Do \(\Delta HMK\backsim\Delta BMC\Rightarrow\widehat{HKM}=\widehat{BCM}\Rightarrow\widehat{GKM}=\widehat{GCM}\).
Xét tứ giác GKCM có \(\widehat{GKM}=\widehat{GCM}\) nên GKCM là tứ giác nội tiếp.
Khi đó \(\widehat{MGC}=\widehat{MKC}=90^o\) hay \(MG\perp BC.\)
Cho đường tròn $(O)$. Từ điểm $P$ nằm ngoài đường tròn, kẻ hai tiếp tuyến $PA$, $PB$ với $(O)$.
a/ Trên đoạn $AB$ lấy điểm $M$ (khác $A$ và $B$). Qua $M$ kẻ đường vuông góc với $OM$ cắt $PA$, $PB$ tại $C$ và $D$. Chứng minh $MC = MD$.
b/ Trên cung nhỏ $AB$ lấy điểm $I$ ($I$ khác $A$ và $B$). Gọi hình chiếu vuông góc của $I$ lên $BA$, $PB$, $PA$ theo thứ tự là $H$, $K$, $L$. Chứng minh \(\Delta HIL\sim\Delta KIH\) và $KH.IL = IH.HL$.
Hướng dẫn giải:

a) Xét tứ giác CAMO có \(\widehat{CAO}=\widehat{CMO}=90^o\) nên CAMO là tứ giác nội tiếp. Khi đó \(\widehat{OCM}=\widehat{OAM}\) (Hai góc nội tiếp cùng chắn cung OM).
Xét tứ giác OMDB có \(\widehat{OMD}+\widehat{OBD}=180^o\) nên OMDB là tứ giác nội tiếp. Khi đó \(\widehat{MDO}=\widehat{MBO}\) (Hai góc nội tiếp cùng chắn cung MO).
Lại có tam giác OAB có OA = OB nên nó là tam giác cân. Vậy thì \(\widehat{MAO}=\widehat{MBO}\).
Suy ra \(\widehat{MCO}=\widehat{MDO}\) hay tam giác OCD cân tại O.
Do OM là đường cao từ đỉnh cân nên OM cũng là đường trung tuyến. Vậy nên MC = MD.
b) Xét tứ giác HILA có \(\widehat{AHI}+\widehat{ILA}=180^o\) nên HILA là tứ giác nội tiếp. Vậy thì \(\widehat{IHL}=\widehat{IAL}\) (Hai góc nội tiếp cùng chắn cung IL)
Ta cũng có tứ giác BKIH nội tiếp \(\left(\widehat{BHI}+\widehat{BKI}=180^o\right)\) nên \(\widehat{HBI}=\widehat{HKI}\) (Hai góc nội tiếp cùng chắn cung HI)
Mà \(\widehat{HAI}=\widehat{BAI}=\widehat{IBK}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung IB)
Nên \(\widehat{IHL}=\widehat{IKH}\).
Hoàn toàn tương tự ta có :
\(\widehat{ILH}=\widehat{IAH}=\widehat{KBI}=\widehat{IHK}\).
Xét tam giác HIL và tam giác KIB có :
\(\widehat{IHL}=\widehat{IKH}\) và \(\widehat{ILH}=\widehat{IHK}\) nên \(\Delta HIL\backsim\Delta KIH\left(g-g\right)\)
\(\Rightarrow\dfrac{HL}{KH}=\dfrac{IL}{IH}\Rightarrow KH.IL=IH.HL\) (đpcm).
Cho tam giác $ABC$ nội tiếp trong đường tròn $(O)$. Từ một điểm $M$ bất kỳ trên $(O)$, kẻ $MP$, $MQ$, $MR$ lần lượt vuông góc với $BC$, $CA$, $AB$. Chứng minh $P$, $Q$, $R$ thẳng hàng.
Hướng dẫn giải:

Ta thấy tứ giác RBPM có \(\widehat{MRB}+\widehat{MPB}=180^o\) nên RBPM là tứ giác nội tiếp.
Vậy nên \(\widehat{MRP}=\widehat{MBP}\) (Hai góc nội tiếp cùng chắn cung MP)
Tứ giác ABMC nội tiếp nên \(\widehat{MBC}=\widehat{MAC}\) (Hai góc nội tiếp cùng chắn cung MC)
Suy ra \(\widehat{MRP}=\widehat{MAC}\).
Tứ giác MRAQ có \(\widehat{MRA}+\widehat{MQA}=180^o\) nên MRAQ là tứ giác nội tiếp. Suy ra \(\widehat{MRQ}=\widehat{MAQ}\) (Hai góc nội tiếp cùng chắn cung MQ)
Vậy thì \(\widehat{MRP}=\widehat{MRQ}\) hay R, P, Q thẳng hàng.
Cho đường tròn $(O; R)$ tiếp xúc với đường thẳng $d$ tại $A$. Trên $d$ lấy điểm $H$ không trùng với điểm $A$ và $AH < R$. Qua $H$ kẻ đường thẳng vuông góc với $d$, đường thẳng này cắt đường tròn tại hai điểm $E$ và $B$ ($E$ nằm giữa $B$ và $H$).
a) Chứng minh \(\widehat{ABE}=\widehat{EAH}\) và \(\Delta ABH\backsim\Delta AEH\).
b) Lấy điểm $C$ trên $d$ sao cho $H$ là trung điểm của đoạn $AC$, đường thẳng $CE$ cắt $AB$ tại $K$. Chứng minh $AHEK$ là tứ giác nội tiếp.
c) Xác định vị trí điểm $H$ để \(AB=R\sqrt{3}\).
Hướng dẫn giải:
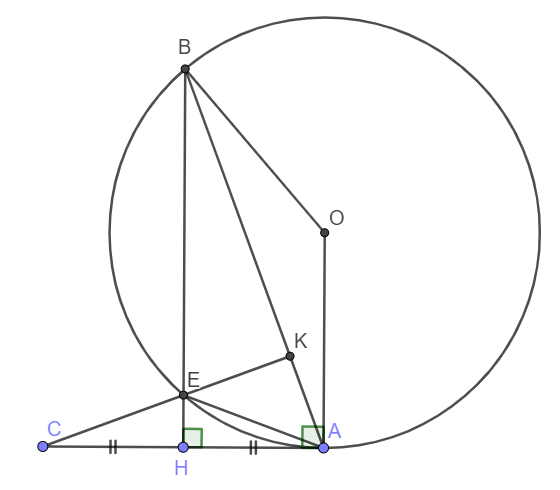
a) Xét đường tròn (O) ta có \(\widehat{ABE}=\widehat{EAH}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn một cung)
Xét tam giác \(\Delta ABH\) và \(\Delta AEH\) có:
\(\widehat{ABH}=\widehat{EAH}\)
Góc H chung
\(\Rightarrow\Delta ABH\backsim\Delta AEH\left(g-g\right)\)
b) Ta thấy BH vuông góc với AC tại trung điểm H nên HB là trung trực của AC. Vậy thì EA = EC hay \(\widehat{EAH}=\widehat{ECH}\).
Mà \(\widehat{EAH}=\widehat{ABH}\Rightarrow\widehat{ACK}=\widehat{ABH}\).
Vì \(\widehat{ABH}+\widehat{BAH}=90^o\Rightarrow\widehat{ACK}+\widehat{BAH}=90^o\Rightarrow\widehat{AKC}=90^o\).
Xét tứ giác AKEH có \(\widehat{AKE}+\widehat{AHE}=180^o\) nên AKEH là tứ giác nội tiếp.
c) Xét hình thang vuông AOBH, ta có:
\(OA=OB=R;AB=R\sqrt{3}\).
\(cos\widehat{OAB}=\dfrac{\dfrac{R\sqrt{3}}{2}}{R}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{OAB}=30^o.\)
\(\Rightarrow\widehat{BAH}=60^o.\)
Xét tam giác vuông ABH, có:\(AB=R\sqrt{3};\widehat{BAH}=60^o\Rightarrow cos60^o=\dfrac{AH}{AB}.\)
\(\Rightarrow AH=AB.cos60^o=R\sqrt{3}.\dfrac{1}{2}=\dfrac{R\sqrt{3}}{2}\).
Vậy khi \(AH=\dfrac{R\sqrt{3}}{2}\) thì \(AB=R\sqrt{3}\).
Cho tam giác $ABC$ có ba góc nhọn nội tiếp đường tròn $(O)$. Các đường cao $AD$, $BE$, $CF$ cắt nhau tại $H$ và cắt đường tròn $(O)$ lần lượt tại $M$, $N$, $P$. Chứng minh rằng:
a) Tứ giác $AEHF$ nội tiếp.
b) Bốn điểm $B$, $C$, $E$, $F$ cùng thuộc một đường tròn.
c) $AE.AC = AH.AD$ và $AD.BC = BE.AC$.
d) $H$ và $M$ đối xứng nhau qua $BC$.
e) Xác định tâm đường tròn nội tiếp tam giác $DEF$.
Hướng dẫn giải:
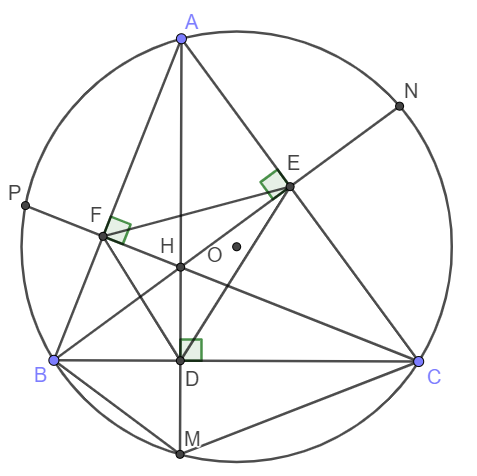
1) Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^o\) nên AEHF là tứ giác nội tiếp.
2) Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^o\) nên BFEC là tứ giác nội tiếp hay B, F, E, C cùng thuộc một đường tròn.
3) Ta thấy ngay \(\Delta AHE\backsim\Delta ACD\left(g-g\right)\)
\(\Rightarrow\dfrac{AE}{AD}=\dfrac{AH}{AC}\Rightarrow AE.AC=AD.AH.\)
Ta thấy ngay \(AD.BC=AC.BE\left(=\dfrac{S_{ABC}}{2}\right)\).
4) Ta thấy \(\widehat{HCB}=\widehat{BAM}\) (Cùng phụ với góc \(\widehat{ABC}\) ).
Do tứ giác ABMC nội tiếp nên \(\widehat{BAM}=\widehat{BCM}\) (Góc nội tiếp cùng chắn cung BM)
Vậy nên \(\widehat{MCB}=\widehat{BCH}\) hay CD là đường phân giác của tam giác HCM.
Lại có CD cũng là đường cao nên HCM là tam giác cân tại C. Vậy CB cũng là trung trực của HM hay H, M đối xứng qua D.
5) Do BFHD là tứ giác nội tiếp nên \(\widehat{FDH}=\widehat{FBH}=\widehat{ABE}\) (Góc nội tiếp)
Lại có \(\widehat{ABE}=\widehat{ACF}=\widehat{ECH}\) (Cùng phụ với góc BAC)
Tứ giác DHEC cũng nội tiếp nên \(\widehat{ECH}=\widehat{EDH}\) (Góc nội tiếp)
Từ đó ta có :
\(\widehat{HDF}=\widehat{HDE}\) hay DH là phân giác góc \(\widehat{EDF}\).
Tương tự FH cũng là phân giác góc \(\widehat{DFE}\)
Từ đó suy ra H là tâm đường tròn nội tiếp tam giác EFD.
Từ điểm $M$ nằm ngoài đường tròn $(O)$ vẽ hai tiếp tuyến $MA$ và $MB$ với đường tròn đó. Trên cung nhỏ $AB$ lấy điểm $C$. Vẽ \(CD\perp AB\), \(CE\perp MA\), \(CF\perp MB\). Gọi $I$ là giao điểm của $AC$ và $DE$, $K$ là giao điểm của $BC$ và $DF$. Chứng minh rằng :
a) Tứ giác $AECD$, $BFCD$ nội tiếp được.
b) $CD^2 = CE.CF$.
c) \(IK\perp CD\).
Hướng dẫn giải:

a) Xét tứ giác AECD có \(\widehat{AEC}+\widehat{ADC}=180^o\) nên AECD là tứ giác nội tiếp.
Xét tứ giác DCFB có \(\widehat{CDB}+\widehat{CFB}=180^o\) nên DCFB là tứ giác nội tiếp.
b) Ta có \(\widehat{EDC}=\widehat{EAC}\) (Hai góc nội tiếp cùng chắn cung EC)
\(\widehat{EAC}=\widehat{ABC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn một cung)
\(\widehat{ABC}=\widehat{DFC}\) (Hai góc nội tiếp cùng chắn cung DC)
Nên \(\widehat{EDC}=\widehat{DFC}\).
Tương tự \(\widehat{DEC}=\widehat{FDC}\).
Xét tam giác EDC và tam giác DFC có : \(\widehat{EDC}=\widehat{DFC}\) và \(\widehat{DEC}=\widehat{FDC}\) nên \(\Delta EDC\backsim\Delta DFC\left(g-g\right)\)
\(\Rightarrow\dfrac{EC}{DC}=\dfrac{DC}{FC}\Rightarrow DC^2=CE.CF\).
c) Xét tam giác vuông DCB có \(\widehat{DBC}+\widehat{DCB}=90^o\).
Mà \(\widehat{DBC}=\widehat{EAC}=\widehat{IDC}\Rightarrow\widehat{DCK}+\widehat{IDC}=90^o\).
Tương tự \(\widehat{ICD}+\widehat{CDK}=90^o\).
Từ đó ta có \(\widehat{IDK}+\widehat{ICK}=180^o\) hay DICK là tứ giác nội tiếp.
\(\Rightarrow\widehat{IKC}=\widehat{IDC}\).
Mà \(\widehat{IDC}=\widehat{DBC}\), chúng lại ở vị trí đồng vị nên IK//AB.
Mà \(AB\perp DC\Rightarrow IK\perp DC\).
Cho tam giác $ABC$ có các góc đều nhọn và \(\widehat{A}=45^o\). Vẽ đường cao $BD$ và $CE$ của tam giác $ABC$. Gọi $H$ là giao điểm của $BD$ và $CE$.
a) Chứng minh tứ giác $ADHE$ nội tiếp.
b) Tính tỉ số \(\dfrac{DE}{BC}\).
c) Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Chứng minh \(OA\perp DE\).
Hướng dẫn giải:

a) Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=180^o\) nên ADHE là tứ giác nội tiếp.
b) Xét tam giác ADB và tam giác AEC có :
Góc A chung
\(\widehat{ADB}=\widehat{AEC}=90^o\)
\(\Rightarrow\Delta ABD\backsim\Delta ACE\left(g-g\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\).
Từ đó ta suy ra \(\Delta AED\backsim\Delta ACB\left(c-g-c\right)\)
Vậy thì \(\dfrac{ED}{CB}=\dfrac{AD}{AB}\).
Xét tam giác vuông ADB có \(\dfrac{AD}{AB}=cos45^o=\dfrac{\sqrt{2}}{2}\)
Vậy nên \(\dfrac{ED}{BC}=\dfrac{\sqrt{2}}{2}\).
c) Kẻ tiếp tuyến Ax.
Ta thấy rằng \(\widehat{BAx}=\widehat{BCA}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn một cung)
Mà \(\widehat{BCA}=\widehat{AED}\) (Do \(\Delta AED\backsim\Delta ACB\) )
nên \(\widehat{BAx}=\widehat{AED}\).
Chúng lại ở vị trí so le trong nên $DE//Ax$.
Do \(Ax\perp AO\) nên \(ED\perp AO\).
Cho tam giác nhọn $ABC$. Gọi $H$ là chân đường cao hạ từ $A$ xuống cạnh $BC$. Đường tròn đường kính $BC$ cắt $AB$, $AC$ lần lượt tại $D$ và $E$. Nối $H$ với $E$ cắt đường tròn đường kính $BC$ tại điểm thứ hai $F$.
a) Chứng minh rằng bốn điểm $H$, $B$, $A$, $E$ cùng nằm trên một đường tròn. Hãy xác định tâm và bán kính đường tròn ấy.
b) Chứng minh \(DF\perp BC.\)
c) Gọi $I$ là điểm đối xứng với $E$ qua $BC$. Chứng minh rằng $HD.HI = HE.HF$.
Hướng dẫn giải:
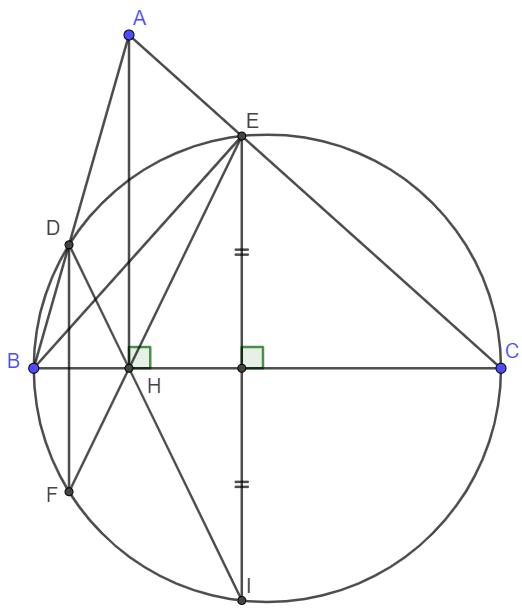
a) Do E thuộc đường tròn đường kính BC nên \(\widehat{BEC}=90^o\Rightarrow\widehat{BEA}=90^o\).
Xét tứ giác HBAE có \(\widehat{AEB}=\widehat{AHB}=90^o\) nên HBAE là tứ giác nội tiếp.
Vậy H, B, A, E cùng thuộc một đường tròn.
Ta thấy ngay H, B, A, E cùng thuộc đường tròn đường kính $AB$, tức là tâm đường tròn là trung điểm $AB$ và bán kính là \(\dfrac{AB}{2}\).
b) Do HBAE là tứ giác nội tiếp nên \(\widehat{BAH}=\widehat{BEH}=\widehat{BEF}\) (Hai góc nội tiếp cùng chắn cung BH)
Lại có \(\widehat{BEF}=\widehat{BDF}\) (Hai góc nội tiếp cùng chắn cung BF)
Vậy nên \(\widehat{BDF}=\widehat{BAH}\).
Chúng lại ở vị trí đồng vị nên DF//AH.
Ta có \(AH\perp BC\Rightarrow DF\perp BC.\)
c) Do E và I đối xứng nhau qua BC nên BC là đường trung trực của IE. Vậy thì HE = HI.
Lại có DF là dây cung của đường tròn đường kính BC, lại có đường kính BC vuông góc với DF nên BC đi qua trung điểm DF. Nói cách khác, BC là trung trực của FD, hay HD = HF.
Vậy ta có ngay HD.HI = HF.HE (đpcm).
Cho hình thang cân $ABCD$ ($AB > CD$; $AB//CD$) nội tiếp đường tròn $(O)$. Tiếp tuyến với đường tròn $(O)$ tại $A$ và $D$ cắt nhau tại $I$. Gọi $E$ là giao điểm của hai đường chéo $AC$ và $BD$.
a) Chứng minh tứ giác $AIDE$ nội tiếp.
b) Chứng minh $AB//IE$.
c) Đường thẳng $IE$ cắt cạnh bên $AD$ và $BC$ của hình thang tương ứng tại $M$ và $N$. Chứng minh rằng:
+ $E$ là trung điểm $MN$.
+ \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{MN}\).
Hướng dẫn giải:

a) Do AB//CD nên \(\stackrel\frown{AD}=\stackrel\frown{BC}\).
Xét tứ giác IAOD có \(\widehat{IAO}=\widehat{IDO}=90^o\) nên \(\widehat{DIA}+\widehat{DOA}=180^o\) (1)
Ta thấy \(\widehat{AED}\) là góc có đỉnh nằm ở bên trong đường tròn nên \(\widehat{AED}=\dfrac{\stackrel\frown{AD}+\stackrel\frown{BC}}{2}=\dfrac{\stackrel\frown{AD}+\stackrel\frown{AD}}{2}=\stackrel\frown{AD}\).
Lại có góc AOD là góc ở tâm chắn cung AD nên \(\widehat{AOD}=\stackrel\frown{AD}\).
Vậy nên \(\widehat{AOD}=\widehat{AED}\) (2)
Từ (1) và (2) suy ra \(\widehat{DIA}+\widehat{DEA}=180^o\).
Xét tứ giác AIDE có \(\widehat{DIA}+\widehat{DEA}=180^o\) nên AIDE là tứ giác nội tiếp.
b) Do AIDE là tứ giác nội tiếp nên \(\widehat{IED}=\widehat{IAD}\) (Hai góc nội tiếp cùng chắn cung ID)
Lại có \(\widehat{IAD}=\widehat{ABD}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn một cung)
Vậy nên \(\widehat{IED}=\widehat{ABD}\). Chúng lại ở vị trí đồng vị nên IE//AB.
c)
+) Do IE//AB nên MN//DC.
Xét hình thang ABCD có MN//AB//CD nên \(\dfrac{DM}{DA}=\dfrac{NC}{BC}\).
Xét tam giác ADB, áp dụng Talet ta có: \(\dfrac{ME}{AB}=\dfrac{DM}{DA}\).
Xét tam giác ACB, áp dụng Talet ta có: \(\dfrac{EN}{AB}=\dfrac{NC}{BC}\).
Vậy nên \(\dfrac{ME}{AB}=\dfrac{NE}{AB}\Rightarrow ME=NE\) hay E là trung điểm MN.
+) Ta có \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{MN}\Leftrightarrow\dfrac{MN}{AB}+\dfrac{MN}{CD}=2\)
\(\Leftrightarrow\dfrac{2ME}{AB}+\dfrac{2NE}{DC}=2\Leftrightarrow\dfrac{ME}{AB}+\dfrac{NE}{DC}=1\).
Áp dụng định lý Ta let ta có:
\(\dfrac{ME}{AB}=\dfrac{ED}{DB};\dfrac{EN}{DC}=\dfrac{EB}{DB}\)
Vậy thì \(\dfrac{ME}{AB}+\dfrac{EN}{DC}=\dfrac{ED}{DB}+\dfrac{EB}{DB}=\dfrac{DB}{DB}=1\) (Đúng)
Từ đó ta có \(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{2}{MN}\) (đpcm).
Cho nửa đường tròn đường kính $BC$, bán kính $R$ và điểm $A$ nằm trên nửa đường tròn ($A$ khác $B$ và $C$). Từ $A$ hạ $AH$ vuông góc với $BC$. Trên nửa mặt phẳng bờ $BC$ chứa điểm $A$, vẽ nửa đường tròn đường kính $BH$ cắt $AB$ tại $E$, nửa đường tròn đường kính $HC$ cắt $AC$ tại $F$.
a) Tứ giác $AFHE$ là hình gì? Vì sao?
b) Chứng minh $BEFC$ là tứ giác nội tiếp.
c) Xác định vị trí của điểm $A$ sao cho tứ giác $AFHE$ có diện tích lớn nhất. Tính diện tích lớn nhất đó theo $R$.
Hướng dẫn giải:

a) Do E, F lần lượt thuộc các nửa đường tròn đường kính BH và CH nên \(\widehat{BEH}=\widehat{CFH}=90^o\Rightarrow\widehat{AEH}=\widehat{AFH}=90^o\).
A cũng thuộc nửa đường tròn đường kính BC nên \(\widehat{BAC}=90^o\).
Xét tứ giác AFHE có \(\widehat{EAF}=\widehat{AEH}=\widehat{AFH}=90^o\) nên nó là hình chữ nhật.
b) Ta thấy ngay AH là tiếp tuyến tại H của nửa đường tròn đường kính BH.
Do AFHE là hình chữ nhật nên \(\widehat{AFE}=\widehat{AHE}\).
Lại thấy \(\widehat{EHA}=\widehat{EBH}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung EH)
Vậy nên \(\widehat{AFE}=\widehat{EBH}\).
Xét tứ giác BEFC có \(\widehat{AFE}=\widehat{EBH}\) nên nó là tứ giác nội tiếp (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện).
c) Do AFHE là hình chữ nhật nên \(S_{AFHE}=2S_{AEF}=2.\dfrac{1}{2}.AE.AF=AE.AF\)
Áp dụng bất đẳng thức Co-si ta có:
\(AE.AF\le\dfrac{AE^2+AF^2}{2}=\dfrac{EF^2}{2}=\dfrac{AH^2}{2}\)
Lại có \(AH\le R\Rightarrow AE.AF\le\dfrac{R^2}{2}\).
Vậy \(maxS_{AFHE}=\dfrac{R^2}{2}\) , khi AH = R hay A là điểm chính giữa cung BC.
Cho tam giác $MNP$ vuông tại $M$. Trên $MP$ lấy điểm $E$ \(\left(E\ne M,E\ne P\right)\). Vẽ đường tròn tâm $I$ đường kính $EP$ cắt $NP$ tại điểm thứ hai là $F$. Nối $NE$ cắt đường tròn tại điểm thứ hai là $H$. $MH$ giao với đường tròn $(I)$ tại điểm $G$. Chứng minh:
a) Tứ giác $MNFE$ nội tiếp.
b) Khi $E$ chuyển động trên $MP$ thì \(\widehat{MHE}\) có số đo không đổi.
c) $MN//GF$.
Hướng dẫn giải:

a) Do F thuộc đường tròn nên \(\widehat{EFP}=90^o\Rightarrow\widehat{NFE}=90^o\).
Xét tứ giác MNFE có \(\widehat{NFE}+\widehat{NME}=90^o+90^o=180^o\)
nên MNFE là tứ giác nội tiếp.
b) Do H thuộc đường tròn đường kính EP nên \(\widehat{NHP}=90^o\).
Xét tứ giác NMHP có \(\widehat{NHP}=\widehat{NMP}=90^o\) nên NMHP là tứ giác nội tiếp.
\(\Rightarrow\widehat{MHE}=\widehat{MHN}=\widehat{MPN}\) (Hai góc nội tiếp cùng chắn cung MN)
Lại có \(\widehat{MPN}\) không đổi nên \(\widehat{MHE}\) cũng không đổi khi E di chuyển trên MP.
c) Do \(\widehat{EHG}=\widehat{FPE}\Rightarrow EG=EF\).
Lại có IG = IF (Cùng bằng \(\dfrac{EP}{2}\))
Vậy EI là trung trực của FG, hay \(FG\perp MP\).
Lại có \(MN\perp MP\) nên FG//MN.
Cho nửa đường tròn $(O;R)$ đường kính $AB$, dây $AC$. Gọi $E$ là điểm chính giữa cung $AC$, bán kính $OE$ cắt $AC$ tại $H$, vẽ $CK$ song song với $BE$ cắt $AE$ tại $K$.
a) Chứng minh tứ giác $CHEK$ nội tiếp.
b) Chứng minh \(KH\perp AB\).
Hướng dẫn giải:

a) Do E là điểm chính giữa cung AC nên H là trung điểm AC.
Vậy thì \(OE\perp AC\).
Do E thuộc nửa đường tròn nên \(\widehat{AEB}=90^o.\).
Do KC//EB nên \(\widehat{EKC}=\widehat{AEB}=90^o\) (Hai góc đồng vị).
Xét tứ giác CHEK có \(\widehat{EKC}+\widehat{EHC}=180^o\) nên CHEK là tứ giác nội tiếp.
b) Gọi giao điểm của KH với AB là I.
Do tứ giác EHCK nội tiếp nên \(\widehat{EKH}=\widehat{ECH}\) (Hai góc nội tiếp cùng chắn cung EH)
Vậy nên: \(\widehat{EKH}+\widehat{EAI}=\widehat{ECA}+\widehat{EAI}=\dfrac{\stackrel\frown{EA}}{2}+\dfrac{\stackrel\frown{EB}}{2}=\dfrac{\stackrel\frown{AB}}{2}=90^o\).
\(\Rightarrow\widehat{AIK}=180^o-90^o=90^o\).
Hay \(HK\perp AB.\)
Cho nửa đường tròn đường kính $MN$ và điểm $P$ bất kỳ thuộc nửa đường tròn ($P$ khác $M$ và $N$). Trên nửa mặt phẳng bờ $MN$ chứa nửa đường tròn, kẻ tiếp tuyến $Mx$. Tia $NP$ cắt $Mx$ tại $I$. Tia phân giác của \(\widehat{IMP}\) cắt nửa đường tròn tại $J$ và cắt tia $NP$ tại $H$. Tia $NJ$ giao tia $Mx$ tại $G$ và giao $MP$ tại $K$.
a) Chứng minh tứ giác $JHPK$ nội tiếp.
b) Chứng minh $IM^2 = IP.IN$.
c) Chứng minh tam giác $MNH$ cân.
d) Chứng minh tứ giác $MKHG$ là hình thoi.
e) Tìm vị trí điểm $P$ sao cho tứ giác $IHKM$ nội tiếp được.
Hướng dẫn giải:
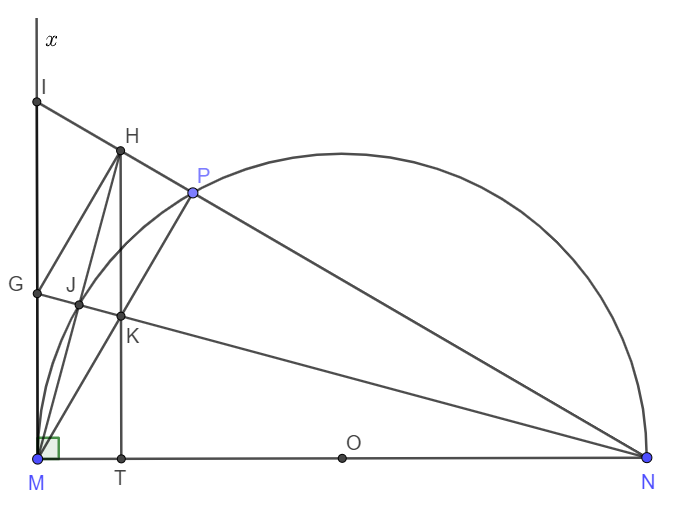
a) Do I và P đều thuộc nửa đường tròn nên \(\widehat{MJN}=\widehat{MPN}=90^o\Rightarrow\widehat{HJK}=\widehat{HPK}=90^o\).
Xét tứ giác JHPK có \(\widehat{HJK}+\widehat{HPK}=180^o\) nên JHPK là tứ giác nội tiếp.
b) Xét tam giác IPM và tam giác IMN có :
\(\widehat{IPM}=\widehat{IMN}=90^o\)
Góc I chung
\(\Rightarrow\Delta IPM=\Delta IMN\left(g-g\right)\)
\(\Rightarrow\dfrac{IP}{IM}=\dfrac{IM}{IN}\Rightarrow IM^2=IP.IN\).
c) Ta thấy góc IMH là góc tạo bởi tiếp tuyến và dây cung nên \(\widehat{IMH}=\dfrac{\stackrel\frown{MJ}}{2}\)
Góc JMP là góc nội tiếp chắn cung JP nên \(\widehat{JMP}=\dfrac{\stackrel\frown{JP}}{2}\).
Mà hai góc này lại bằng nhau nên \(\stackrel\frown{MJ}=\stackrel\frown{JP}\).
\(\Rightarrow\widehat{MNJ}=\widehat{JNP}\) (Hai góc nội tiếp chắn hai cung bằng nhau)
hay NJ là phân giác góc MNH.
Xét tam giác MNH có NJ là phân giác đồng thời đường cao nên tam giác MNH cân tại N.
d) Xét tam giác GMK có MJ là phân giác đồng thời đường cao nên GMK là tam giác cân tại M. Vậy thì MG = MK.
Theo câu c, ta thấy rằng GK là trung trực của MH nên GM = GH ; KM = KH.
Xét tứ giác MKHG có GM = MK = KH = HG nên MKHG là hình thoi.
e) Do MKHG là hình thoi nên GM//HK.
Lại có \(GM\perp MN\Rightarrow HK\perp MN\)
Gọi T là giao điểm của HK và MN \(\Rightarrow\widehat{HTN}=90^o\).
Để tứ giác IHKM nội tiếp thì \(\widehat{IMK}=\widehat{THN}\) (Góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện)
Lại có \(\widehat{IMK}=\widehat{IMP}=\widehat{TNP}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung MP)
Vậy thì \(\widehat{TNH}=\widehat{THN}\).
Xét tam giác vuông HTN có \(\widehat{TNH}=\widehat{THN}\) nên \(\widehat{TNH}=\widehat{THN}=45^o\).
\(\widehat{TNH}=\widehat{MNP}=45^o\) thì P là điểm chính giữa cung MN.
Cho đường tròn $(O)$ đường kính $AB$. Lấy điểm $C$ thuộc đoạn $AO$ ($C$ không trùng $O$ và $A$), vẽ đường tròn $(O')$ đường kính $CB$. Qua trung điểm $M$ của $AC$, kẻ đường thẳng vuông góc với $AC$, cắt $(O)$ tại $D$ và $E$. Gọi $I$ là giao điểm thứ hai của $BD$ với đường tròn $(O')$, $J$ là giao điểm thứ hai của $BE$ với đường tròn $(O')$. Chứng minh:
a) Tứ giác $CDAE$ là hình thoi.
b) $CI//AD$.
c) Ba điểm $E$, $C$, $I$ thẳng hàng.
d) Bốn điểm $M$, $I$, $B$, $E$ cùng thuộc một đường tròn.
e) Ba đường thẳng $AM$, $DJ$, $EI$ đồng quy.
Hướng dẫn giải:
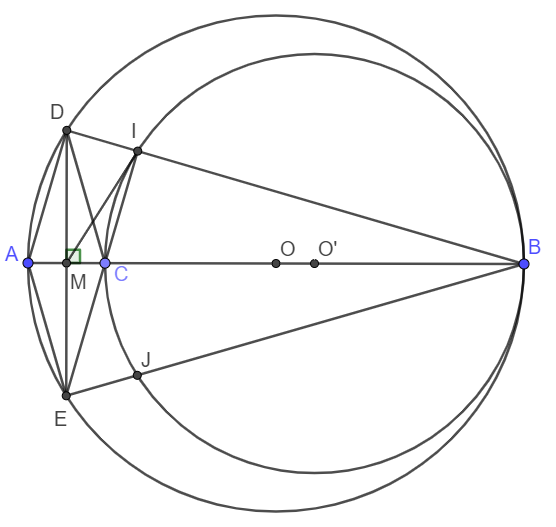
a) Do DE là dây cung, \(OA\perp DE\) nên theo tính chất đường kính dây cung, ta có M là trung điểm DE.
Xét tứ giác CDAE có MA = MC (gt) ; MD = ME (cmt) nên CDAE là hình bình hành.
Lại có \(DE\perp AC\) nên CDAE là hình thoi.
b) I thuộc đường tròn (O') nên \(\widehat{CIB}=90^o\).
D thuộc đường tròn (O) nên \(\widehat{ADB}=90^o\).
Hai góc trên lại ở vị trí đồng vị nên IC//DA.
c) Theo câu a, CDAE là hình thoi nên CE//DA.
Lại theo câu b, IC//DA.
Vậy nên E, C, I thẳng hàng.
d) Do E, C, I thẳng hàng nên \(EI\perp DB\).
Xét tứ giác EMIB có \(\widehat{EMB}=\widehat{EIB}=90^o\) nên tứ giác EMIB nội tiếp. Vậy E, M, I, B cùng thuộc một đường tròn.
e) Xét tam giác EDB có EI và BM là các đường cao nên C là trực tâm tam giác. Vậy DC vuông góc EB.
Lại có CJ vuông góc EB nên D, C, J thẳng hàng.
Vậy thì AM, EI, DJ đồng quy tại điểm C.
